Podręcznik
2. Charakterystyka statyczna
2.1. Przykłady wyznaczania charakterystyki statycznej
W układach regulacji interesuje nas zachowanie obiektu w pobliżu tzw. punktu równowagi obiektu. Potocznie przez punkt równowagi rozumiemy taki stan obiektu, w którym obiekt samoczynnie pozostaje (tzn. "nic się w układzie nie zmienia"). Przypomnijmy równania stanu układu trzech zbiorników
\( \begin{eqnarray} \frac{d H_1(t)}{dt} &=& \frac{1}{A}Q_{we}(t) - \frac{\alpha}{A} \sqrt{H_1(t)-H_2(t)} \qquad(1.85)\\ \frac{d H_2(t)}{dt} &=& \frac{\alpha}{A} \sqrt{H_1(t)-H_2(t)} - \frac{\alpha}{A} \sqrt{H_2(t)-H_3(t)} \qquad(1.86) \\ \frac{d H_3(t)}{dt} &=& \frac{\alpha}{2A} \sqrt{H_2(t)-H_3(t)} - \frac{\alpha}{2A} \sqrt{H_3(t)} \qquad(1.87) \end{eqnarray} \)
W punkcie równowagi sygnały sterujące muszą mieć stałą wartość. W przeciwnym razie zmiany sygnału sterującego będą wymuszać zmiany zmiennych stanu. Oznaczmy wartość sterowania w punkcie pracy jako \( Q_{we0} \). Punktem równowagi dla układu trzech zbiorników nazwiemy taki stan w którym \( H_1(t) \), \( H_2(t) \) oraz \( H_3(t) \) pozostają stałe. Jeżeli wysokości słupów cieczy pozostają stałe, to ich pochodne w punkcie równowagi się zerują. Oznaczmy wartości zmiennych stanu w punkcie równowagi jako \( H_{10} \), \( H_{20} \) oraz \( H_{30} \). Zauważmy, że \( H_{10} \), \( H_{20} \) oraz \( H_{30} \) nie są funkcjami czasu, ale stałymi. Z równań stanu obiektu (1.85)-(1.87) i warunku zerowania się pochodnej otrzymujemy
\( \begin{eqnarray} 0 &=& \frac{1}{A}Q_{we0} - \frac{\alpha}{A} \sqrt{H_{10}-H_{20}} \qquad(1.88) \\ 0 &=& \frac{\alpha}{A} \sqrt{H_{10}-H_{20}} - \frac{\alpha}{A} \sqrt{H_{20}-H_{30}} \qquad(1.89) \\ 0 &=& \frac{\alpha}{2A} \sqrt{H_{20}-H_{30}} - \frac{\alpha}{2A} \sqrt{H_{30}} \qquad(1.90) \end{eqnarray} \)
Powyższe równania mają także prostą interpretację fizyczną. Punkt równowagi w układzie jest wtedy, gdy przepływy \( Q_{we} \), \( Q_{12} \), \( Q_{23} \) oraz \( Q_3 \) są sobie równe.
Układ równań algebraicznych (1.88)-(1.90) składa się z trzech równań, w których mamy cztery niewiadome \( Q_{we0} \), \( H_{10} \), \( H_{20} \) oraz \( H_{30} \). Oznacza to, że układ posiada więcej niż jeden punkt równowagi. Zbiór wszystkich możliwych punktów równowagi obiektu nazywamy charakterystyką statyczną obiektu.
Aby znaleźć równania charakterystyki statycznej przyjmujemy jedną z niewiadomych jako parametr i rozwiązujemy układ równań (1.88)-(1.90) względem pozostałych niewiadomych. Ponieważ naszym ostatecznym celem jest regulacja wielkości wyjściowej, to przyjmujemy jako parametr \( H_{30} \( i wyznaczamy wartości \( Q_{we0} \), \( H_{10} \) oraz \( H_{20} \) jako funkcje \( H_{30} \).
Równania (1.88)-(1.90) są nieliniowe, jednak ich rozwiązanie nie jest trudne. Rozpocznijmy rozwiązywanie układu równań od równania (1.90). Różnica dwóch wyrażeń jest równa zero, tylko wtedy gdy te wyrażenia są sobie równe
\( \begin{equation} \frac{\alpha}{2A} \sqrt{H_{20}-H_{30}} = \frac{\alpha}{2A} \sqrt{H_{30}} \end{equation}\qquad(1.91) \)
Jeżeli wymnożymy obie strony równania przez \( \dfrac{2A}{\alpha} \) to otrzymamy
\( \begin{equation} \sqrt{H_{20}-H_{30}} = \sqrt{H_{30}} \end{equation}\qquad(1.92) \)
Po podniesieniu obu stron równania do kwadratu otrzymujemy
\( \begin{equation} H_{20}-H_{30} = H_{30} \end{equation}\qquad(1.93) \)
czyli
\( \begin{equation} H_{20} = 2H_{30} \qquad(1.94) \end{equation} \)
Okazuje się, że w stanie ustalonym wysokość słupa cieczy w drugim zbiorniku jest dwa razy wyższa niż wysokość wody w trzecim zbiorniku.
Przejdźmy do rozwiązania równania (1.89). Różnica dwóch wyrażeń jest równa zero, tylko wtedy gdy te wyrażenia są sobie równe
\( \begin{equation} \frac{\alpha}{A} \sqrt{H_{10}-H_{20}} = \frac{\alpha}{A} \sqrt{H_{20}-H_{30}} \end{equation}\qquad(1.95) \)
Jeżeli wymnożymy obie strony równania przez \( \dfrac{A}{\alpha} \) to otrzymamy
\( \begin{equation} \sqrt{H_{10}-H_{20}} = \sqrt{H_{20}-H_{30}} \end{equation}\qquad(1.96) \)
Po podniesieniu obu stron równania do kwadratu otrzymujemy
\( \begin{equation} H_{10}-H_{20} = H_{20}-H_{30} \end{equation}\qquad(1.97) \)
czyli
\( \begin{equation} H_{10} = 2H_{20}-H_{30} \end{equation}\qquad(1.98) \)
Korzystając z (1..94) mamy
\( \begin{equation} H_{10} = 2H_{20}-H_{30} = 2\cdot2H_{30}-H_{30} = 3H_{30} \qquad(1.99) \end{equation} \)
Okazuje się, że w stanie ustalonym wysokość słupa cieczy w pierwszym zbiorniku jest trzy razy wyższa niż wysokość wody w trzecim zbiorniku.
Przejdźmy do rozwiązania równania (1.88). Różnica dwóch wyrażeń jest równa zero, tylko wtedy gdy te wyrażenia są sobie równe
\( \begin{equation} \dfrac{1}{A}Q_{we0} = \dfrac{\alpha}{A} \sqrt{H_{10}-H_{20}} \end{equation}\qquad(1.100) \)
Jeżeli wymnożymy obie strony równania przez \( A \) to otrzymamy
\( \begin{equation} Q_{we0} = \alpha\sqrt{H_{10}-H_{20}} \end{equation}\qquad(1.101) \)
Korzystając z (1.94) oraz (1.99) mamy
\( \begin{equation} Q_{we0} = \alpha\sqrt{H_{10}-H_{20}} = \alpha\sqrt{3H_{30}-2H_{30}} = \alpha\sqrt{H_{30}} \qquad(1.102) \end{equation} \)
Zapiszmy razem równania (1.94), (1.99) oraz (1.102)
\( \begin{eqnarray} H_{20} &=& 2H_{30} \qquad(1.103) \\ H_{10} &=& 3H_{30} \qquad(1.104)\\ Q_{we0} &=& \alpha\sqrt{H_{30}} \qquad(1.105) \end{eqnarray} \)
Definiują one charakterystykę statyczną dla układu trzech zbiorników, gdzie parametrem jest \( H_{30} \). Często pod pojęciem charakterystyki statycznej obiektu rozumie się zależność wyjść obiektu od wejść obiektu w stanie ustalonym. Z równania (1.105) mamy
\( \begin{equation} H_{30} = \dfrac{1}{\alpha^2}Q_{we0}^2 \end{equation}\qquad(1.106) \)
Na Rys. 1.8 przedstawiono wejściowo-wyjściową charakterystykę statyczną dla układu trzech zbiorników.
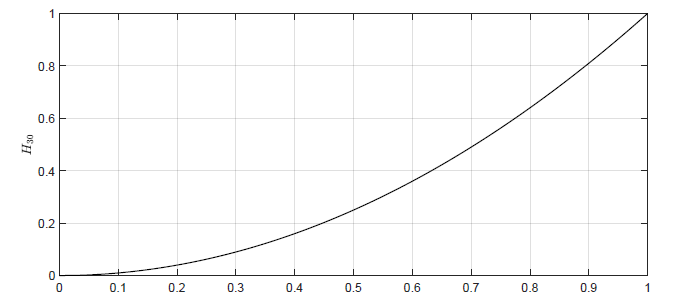
Rysunek 1.8 Wykres charakterystyki statycznej wejściowo-wyjściowej dla układu trzech zbiorników.
Należy jednak pamiętać, że nawet jeżeli w pewnej chwili \( t \) mamy \( Q_{we}(t) = Q_{we0} \) oraz \( H_3(t) = \dfrac{1}{\alpha^2}Q_{we0}^2 \) to obiekt nie musi znajdować się w punkcie równowagi bo możemy mieć \( H_1(t) \neq H_{10} \) lub \( H_2(t) \neq H_{20} \).
Mając równania charakterystyki statycznej możemy przeprowadzić symulację zachowania obiektu w wybranym punkcie równowagi. Przyjmujemy parametry obiektu \( A = 0.5 \), \( \alpha = 1 \). Wybieramy punkt równowagi odpowiadający \( H_{30}=0.25 \). Z równań charakterystyki statycznej otrzymujemy \( H_{20}=0.75 \), \( H_{20}=0.5 \) oraz \( Q_{we0} = 0.5 \). Na Rys. 1.9 przedstawiono trajektorie stanów obiektu dla stałego sterowania \( Q_{we}(t) = Q_{we0} = 0.5 \) i warunków początkowych równych wartościom stanów w wybranym punkcie równowagi \( H_1(t_0) =H_{30}=0.75 \), \( H_2(t_0) =H_{20}=0.5 \), \( H_3(t_0)=H_{30}=0.25 \)
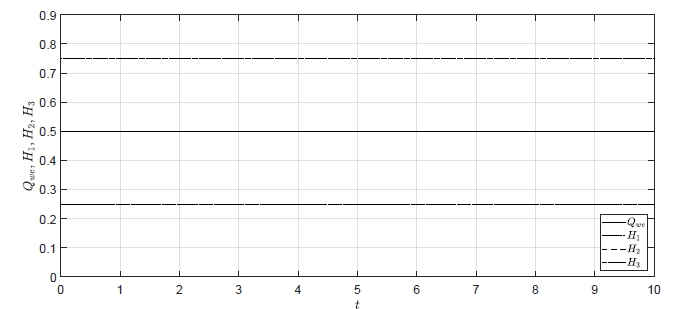
Rysunek 1.9 Trajektorie poziomów cieczy w zbiornikach w punkcie równowagi.
Zgodnie z oczekiwaniami w punkcie równowagi nie następują zmiany poziomów cieczy w zbiornikach. Zauważmy, że trajektorie stanu na Rys. 1.2 i 1.3 dążą dokładnie do wartości obliczonych z charakterystyki statycznej obiektu. Z kolei na Rys. 1.4 poziomy cieczy w zbiornikach wykonują oscylacje wokół wartości poziomów w punkcie równowagi.
\( \begin{eqnarray} \frac{d\theta(t)}{dt} &=& \omega(t) \qquad(1.107) \\ \frac{d\omega(t)}{dt} &=& \frac{g}{l}sin\theta(t) - \frac{D}{ml^2} \omega(t) +\frac{1}{ml^2} M(t) \qquad(1.108) \end{eqnarray} \)
Oznaczmy wartość sterowania w punkcie pracy jako \( M_0 \). Punktem równowagi dla wahadła nazwiemy taki stan w którym \( \theta(t) \) oraz \( \omega(t) \) pozostają stałe, a ich pochodne się zerują. Oznaczmy wartości zmiennych stanu w punkcie równowagi jako \( \theta_0 \) oraz \( \omega_0 \). Z równań stanu obiektu (1.107)-(1.108) i warunku zerowania się pochodnej otrzymujemy
\( \begin{eqnarray} 0 &=& \omega_0 \qquad(1.109) \\ 0 &=& \frac{g}{l}sin\theta_0 - \frac{D}{ml^2} \omega_0 +\frac{1}{ml^2} M_0 \qquad(1.110) \end{eqnarray} \)
Powyższe równania mają następującą interpretację fizyczną. W punkcie równowagi wahadło się nie porusza, a momenty sił działające na wahadło się równoważą.
Układ równań algebraicznych (1.109)-(1.110)) składa się z dwóch równań, w których mamy trzy niewiadome \( M_0 \), \( \theta_0 \) oraz \( \omega_0 \). Przyjmujemy jako parametr wielkość wyjściową \( \theta_0 \) i wyznaczamy wartości \( M_0 \) oraz \( \omega_0 \) jako funkcje \( \theta_0 \).
Z równania (1.109))
\( \begin{equation} \omega_0 = 0 \end{equation}\qquad (1.111) \)
Z równania (1.110)
\( \begin{equation} 0 = \frac{g}{l}sin\theta_0 - \frac{D}{ml^2} \omega_0 +\frac{1}{ml^2} M_0 \end{equation}\qquad(1.112) \)
Korzystając z (1.111)) otrzymujemy
\( \begin{equation} 0 = \dfrac{g}{l}sin\theta_0 +\dfrac{1}{ml^2} M_0 \end{equation}\qquad(1.113) \)
i stąd mamy
\( \begin{equation} \frac{1}{ml^2} M_0 = -\frac{g}{l}sin\theta_0 \end{equation}\qquad(1.114) \)
Mnożąc obie strony powyższego równania przez \( ml^2 \) otrzymujemy
\( \begin{equation} M_0 = -mglsin\theta_0 \qquad(1.115) \end{equation} \)
Zapiszmy razem równania (1.111) oraz (1.115))
\( \begin{eqnarray} \omega_0 &=& 0 \qquad(1.116)\\ M_0 &=& -mglsin\theta_0 \qquad(1.117) \end{eqnarray} \)
Definiują one charakterystykę statyczną dla wahadła. Równanie charakterystyki statycznej typu wejście-wyjście otrzymujemy z równania (1.115))
\( \begin{equation} sin\theta_0 = -\dfrac{1}{mgl}M_0 \end{equation}\qquad(1.118) \)
Z powyższego warunku mamy, że dla \( | M_0| > mgl \) układ nie ma punktów równowagi (moment siły \( M \) jest tak duży, że powoduje ciągłe obracanie się wahadła). Z kolei jeżeli \( | M_0| < mgl \) to układ ma dwa punkty równowagi
\( \begin{eqnarray} \theta_0 &=& arcsin \left(-\frac{1}{mgl}M_0\right) \qquad(1.119)\\ \theta_0 &=& \pi - arcsin \left(-\frac{1}{mgl}M_0\right)\qquad(1.120) \end{eqnarray} \)
Na Rys. 1.10 przedstawiono wejściowo-wyjściową charakterystykę statyczną dla wahadła.
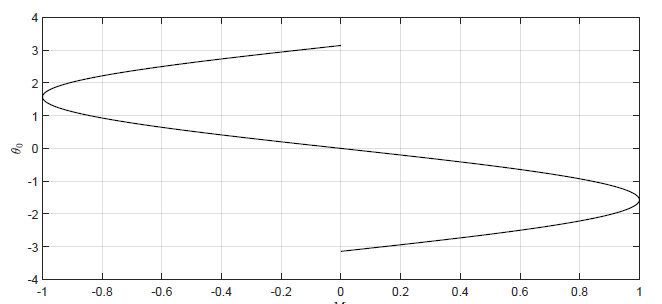
Rysunek 1.10Wykres charakterystyki statycznej wejściowo-wyjściowej dla wahadła.
Należy jednak pamiętać, że nawet jeżeli w pewnej chwili \( t \) mamy \( M(t) = M_0 \) oraz \( sin\theta_0 = \frac{1}{mgl}M_0 \) to obiekt nie musi znajdować się w punkcie równowagi bo możemy mieć \( \omega(t) \neq \omega_0 = 0 \).
Mając równania charakterystyki statycznej możemy przeprowadzić symulację zachowania obiektu w wybranym punkcie równowagi. Przyjmujemy parametry obiektu \( m = 0.1 \), \( l = 1 \), \( g = 10 \), \( D = 0.1 \). Wybieramy punkt równowagi odpowiadający \( \theta=\frac{5\pi}{6} \). Z równań charakterystyki statycznej otrzymujemy \( \omega_0=0 \) oraz \( M_{0} = -0.5 \). Na Rys. 1.11 przedstawiono trajektorie stanów obiektu dla stałego sterowania \( M(t) = M_{0} = -0.5 \( i warunków początkowych równych wartościom stanów w wybranym punkcie równowagi \( \theta(t_0) =\theta_0=\frac{5\pi}{6} \), \( \omega(t_0) =\omega_0=0 \(
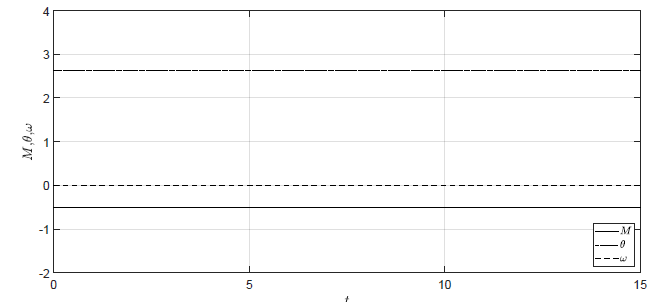
Rysunek 1.11 Trajektorie położenia i prędkości kątowej wahadła w punkcie równowagi.
Zgodnie z oczekiwaniami w punkcie równowagi wahadło nie zmienia swojego położenia, a jego prędkość kątowa wynosi 0. Zauważmy, że trajektorie stanu na Rys. 1.6 dążą dokładnie do wartości obliczonych z charakterystyki statycznej obiektu. Z kolei na Rys. 1.7 zmienne stanu wykonują oscylacje wokół odpowiednich wartości w punkcie równowagi.