Podręcznik

Aby zbadać stabilność punktu równowagi $x_0$ nieliniowego obiektu autonomicznego stosujemy następujący schemat

1.  określamy zlinearyzowane równania stanu w punkcie równowagi $x_0$
2. obliczamy współczynniki wielomianu charakterystycznego
3. stosujemy kryterium Hurwitza, aby sprawdzić czy spełnione są warunki (3.24) oraz (3.25) 

Zastosujmy powyższy schemat do badania stabilności punktów równowagi autonomicznych, nieliniowych obiektów i układów regulacji.

Równania stanu dla układu trzech zbiorników ze stałym sterowaniem  $Q_{we}(t) = Q_{we0}$ (obiekt autonomiczny) mają postać 

$\begin{eqnarray} \dfrac{d H_1(t)}{dt} &=& \dfrac{1}{A}Q_{we0} - \dfrac{\alpha}{A} \sqrt{H_1(t)-H_2(t)} \qquad(3.26)\\ \dfrac{d H_2(t)}{dt} &=& \dfrac{\alpha}{A} \sqrt{H_1(t)-H_2(t)} - \dfrac{\alpha}{A} \sqrt{H_2(t)-H_3(t)} \qquad(3.27)\\ \dfrac{d H_3(t)}{dt} &=& \dfrac{\alpha}{2A} \sqrt{H_2(t)-H_3(t)} - \dfrac{\alpha}{2A} \sqrt{H_3(t)} \qquad(3.28) \end{eqnarray}$

Równania punktu równowagi mają postać

$\begin{eqnarray} H_{20} &=& 2H_{30} \qquad(3.29) \\ H_{10} &=& 3H_{30} \qquad(3.30)\\ Q_{we0} &=& \alpha\sqrt{H_{30}} \qquad(3.31) \end{eqnarray}$

Sterowanie w obiekcie zlinearyzowanym jest równe zero

$\begin{equation} \tilde{Q}_{we} = Q_we(t) - Q_{we0} = Q_{we0} - Q_{we0} = 0 \qquad(3.32)\end{equation}$

Zlinearyzowane równania stanu dla obiektu autonomicznego mają zatem postać 

$\begin{equation}\left(\begin{array}{c}\dfrac{d\tilde{H}_1}{dt}\\ \dfrac{d\tilde{H}_2}{dt}  \\  \dfrac{d\tilde{H}_3}{dt}\end{array}\right) = \left(\begin{array}{ccc}\dfrac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} & \dfrac{\alpha}{2A\sqrt{H_{10}-H_{20}}} & 0 \\\dfrac{\alpha}{2A\sqrt{H_{10}-H_{20}}} &   \dfrac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} + \dfrac{-\alpha}{2A\sqrt{H_{20}-H_{30}}}  &   \dfrac{\alpha}{2A\sqrt{H_{20}-H_{30}}} \\0 &  \dfrac{\alpha}{4A\sqrt{H_{20}-H_{30}}} &  \dfrac{-\alpha}{4A\sqrt{H_{20}-H_{30}}} +  \dfrac{-\alpha}{4A\sqrt{H_{30}}} \end{array}\right)\left(\begin{array}{c}\tilde{H}_1\\  \tilde{H}_2 \\  \tilde{H}_3\end{array}\right) \qquad(3.33)\end{equation}$

Z równań punktu równowagi wynika, że  

$\begin{eqnarray}H_{10}-H_{20} &=& 3H_{30}-2H_{30} = H_{30} \qquad(3.34)  \\H_{20}-H_{30} &=& 2H_{30}-H_{30} = H_{30}  \qquad(3.35)\end{eqnarray}$

Wprowadźmy te zależności do zlinearyzowanych równań stanu

$\begin{equation}\left(\begin{array}{c}\dfrac{d\tilde{H}_1}{dt}\\ \dfrac{d\tilde{H}_2}{dt}  \\  \dfrac{d\tilde{H}_3}{dt}\end{array}\right) = \left(\begin{array}{ccc}\dfrac{-\alpha}{2A\sqrt{H_{30}}} & \dfrac{\alpha}{2A\sqrt{H_{30}}} & 0 \\\dfrac{\alpha}{2A\sqrt{H_{30}}} &   \dfrac{-\alpha}{2A\sqrt{H_{30}}} + \dfrac{-\alpha}{2A\sqrt{H_{30}}}  &   \dfrac{\alpha}{2A\sqrt{H_{30}}} \\0 &  \dfrac{\alpha}{4A\sqrt{H_{30}}} &  \dfrac{-\alpha}{4A\sqrt{H_{30}}} +  \dfrac{-\alpha}{4A\sqrt{H_{30}}} \end{array}\right)\left(\begin{array}{c}\tilde{H}_1\\  \tilde{H}_2 \\  \tilde{H}_3\end{array}\right) \end{equation} \qquad(3.36)$

Wprowadźmy następujące oznaczenie

$\begin{equation}a = \dfrac{\alpha}{4A\sqrt{H_{30}}} >0\qquad(3.37)\end{equation}$

Zlinearyzowane równania stanu mogą zostać zapisane jako

$\begin{equation}\left(\begin{array}{c}\dfrac{d\tilde{H}_1}{dt}\\ \dfrac{d\tilde{H}_2}{dt}  \\  \dfrac{d\tilde{H}_3}{dt}\end{array}\right) = \left(\begin{array}{ccc}-2a & 2a & 0 \\2a &  -4a &  2a \\0 &  a &  -2a\end{array}\right)\left(\begin{array}{c}\tilde{H}_1\\  \tilde{H}_2 \\  \tilde{H}_3\end{array}\right) \end{equation} \qquad(3.38)$

Obliczmy wielomian charakterystyczny dla macierzy obiektu zlinearyzowanego

$\begin{equation}A = \left(\begin{array}{ccc}-2a & 2a & 0 \\2a &  -4a &  2a \\0 &  a &  -2a\end{array}\right)\end{equation} \qquad(3.39)$

Wielomian charakterystyczny wynosi 

$\begin{eqnarray}W(s) &=& det(sI-A) = det \left(s\left(\begin{array}{ccc}1 & 0 & 0 \\0 &  1 &  0 \\0 &  0 &  1\end{array}\right) - \left(\begin{array}{ccc}-2a & 2a & 0 \\2a &  -4a &  2a \\0 &  a &  -2a\end{array}\right) \right)     \nonumber \\&=& det \left(\left(\begin{array}{ccc}s & 0 & 0 \\0 &  s &  0 \\0 &  0 &  s\end{array}\right) - \left(\begin{array}{ccc}-2a & 2a & 0 \\2a &  -4a &  2a \\0 &  a &  -2a\end{array}\right) \right)       \\&=& det \left(\begin{array}{ccc}s+2a & -2a & 0 \\-2a &  s+4a &  -2a \\0 &  -a &  s+2a\end{array}\right) \nonumber\end{eqnarray}\qquad(3.40)$

Wyznacznik macierzy rozmiaru $3\times 3$ może być obliczony z następującego wzoru

$\begin{eqnarray}det \left(\begin{array}{ccc}a_{11} & a_{12} & a_{13}\\a_{21} &  a_{22} &  a_{23} \\a_{31} &  a_{32} &  a_{33}\end{array}\right) &=& a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} \\&& - a_{13}a_{22}a_{31} - a_{11}a_{23}a_{32} - a_{12}a_{21}a_{33}  \end{eqnarray}\qquad(3.41)$

Mamy zatem 

$\begin{eqnarray}W(s) &=& det(sI-A) = det \left(\begin{array}{ccc}s+2a & -2a & 0 \\-2a &  s+4a &  -2a \\0 &  -a &  s+2a\end{array}\right)  \\&=& (s+2a)(s+4a)(s+2a) + (-2a)(-2a)\cdot 0 + 0\cdot (-2a)(-a)  \\&& - 0 \cdot (s+4a) \cdot 0 - (s+2a)(-2a)(-a) - (-2a)(-2a)(s+2a)  \\&=& (s^2+6as+8a^2)(s+2a) - (s+2a)\cdot 2a^2 - 4a^2(s+2a) \nonumber \\&=& s^3+8as^2+20a^2s+16a^3 - 2a^2s-4a^3 - 4a^2s - 8a^3  \\&=& s^3+8as^2+14a^2s+4a^3\end{eqnarray}\qquad(3.42)$

Współczynniki wielomianu charakterystycznego wynoszą

$\begin{equation}a_3 = 1,\ a_2 = 8a,\ a_1 = 14a^2,\ a_0 = 4a^3\end{equation} \qquad(3.43)$

Tworzymy teraz macierz Hurwitza dla wielomianu charakterystycznego. Macierz Hurwitza ma rozmiar $3\times 3$ i postać

$\begin{equation}H = \left(\begin{array}{ccc}a_2 & a_3 & 0 \\a_0 &  a_1 & a_2 \\0 &  0 &  a_0\end{array}\right) = \left(\begin{array}{ccc}8a & 1 & 0 \\4a^3 &  14a^2 & 8a \\0 &  0 & 4a^3\end{array}\right)\end{equation} \qquad(3.44)$

Minory główne macierzy Hurwitza wynoszą

$\begin{equation}|8a|,\ \left|\begin{array}{cc}8a & 1  \\4a^3 &  14a^2 \end{array}\right|,\ \left|\begin{array}{ccc}8a & 1 & 0 \\4a^3 &  14a^2 & 8a \\0 &  0 & 4a^3\end{array}\right|\end{equation} \qquad(3.45)$

Wykorzystujemy teraz Kryterium Hurwitza do sprawdzenia stabilności punktu równowagi układu trzech zbiorników

•   ponieważ $a>0$ to wszystkie współczynniki wielomianu charakterystycznego są dodatnie

              $\begin{equation}a_3 = 1>0,\ a_2 = 8a>0,\ a_1 = 14a^2>0,\ a_0 = 4a^3>0  \end{equation} \qquad(3.46)$

• minory główne macierzy Hurwitza wynoszą

              $\begin{eqnarray}  |8a| &=& 8a >0 \qquad(3.47)\\    \left|   \begin{array}{cc}   8a & 1  \\    4a^3 &  14a^2     \end{array}    \right| &=& 8a\cdot 14a^2 - 1\cdot 4a^3 = 112a^3 - 4a^3 = 108a^3 > 0   \qquad(3.48)\\     \left|   \begin{array}{ccc}   8a & 1 & 0 \\  4a^3 &  14a^2 & 8a \\   0 &  0 & 4a^3  \end{array}  \right| &=& 8a \cdot 14a^2 \cdot 4a^3 + 1\cdot 8a \cdot 0 + 0\cdot 4a^3 \cdot 0 \\   && - 0\cdot 14a^2 \cdot 0 - 8a \cdot 8a \cdot 0 - 1\cdot 4a^3\cdot 4a^3 \nonumber \\   &=& 448a^6 -16a^6 = 432a^6 >0 \nonumber   \end{eqnarray}\qquad(3.49)$

Mamy zatem spełniony warunek dla pierwiastków wielomianu charakterystycznego trzeciego stopnia

$\begin{equation} Re(s_1) < 0,\ Re(s_2) < 0,\ Re(s_3) < 0 \end{equation} \qquad(3.50)$

Punkt równowagi obiektu zlinearyzowanego $\tilde{H}_{10} = 0$, $\tilde{H}_{20} = 0$, $\tilde{H}_{20} = 0$ jest stabilny asymptotycznie. Z drugiej metody Lapunowa mamy zatem, że punkt równowagi obiektu nieliniowego  $H_{10}$, $H_{20}$, $H_{30}$ ze stałym sterowaniem $Q_{we0}$ jest stabilny asymptotycznie. Obliczenia były prowadzone dla dowolnego punktu równowagi w układzie trzech zbiorników. Wynika z tego, że wszystkie punkty równowagi tego układu są stabilne asymptotycznie. Ten wynik jest w zgodzie z wynikami symulacji (Rys. 1.3, 1.12). 

Zbadajmy teraz stabilność punktu pracy układu regulacji trzech zbiorników z regulatorem P. Równania stanu dla układu regulacji mają postać

$\begin{eqnarray}\dfrac{d H_1(t)}{dt} &=& \dfrac{1}{A}\left(k_p(H_3(t)-H_{30}) + Q_{we0} \right) - \dfrac{\alpha}{A} \sqrt{H_1(t)-H_2(t)} \qquad(3.51) \\\dfrac{d H_2(t)}{dt} &=& \dfrac{\alpha}{A}  \sqrt{H_1(t)-H_2(t)} - \dfrac{\alpha}{A}  \sqrt{H_2(t)-H_3(t)} \qquad(3.52) \\\dfrac{d H_3(t)}{dt} &=& \dfrac{\alpha}{2A} \sqrt{H_2(t)-H_3(t)} - \dfrac{\alpha}{2A} \sqrt{H_3(t)} \qquad(3.53)\end{eqnarray}$

Rozważamy punkt pracy określony przez $H_{10}$, $H_{20}$, $H_{30}$ orz $Q_{we0}$. Zlinearyzowane równania stanu (2.22)-(2.24) dla układu regulacji zapisane w postaci macierzowej mają postać

$\begin{equation}\left(\begin{array}{c}\dfrac{d\tilde{H}_1}{dt}\\ \dfrac{d\tilde{H}_2}{dt}  \\  \dfrac{d\tilde{H}_3}{dt}\end{array}\right) = \left(\begin{array}{ccc}\dfrac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} & \dfrac{\alpha}{2A\sqrt{H_{10}-H_{20}}} & \dfrac{k_p}{A} \\\dfrac{\alpha}{2A\sqrt{H_{10}-H_{20}}} &   \dfrac{-\alpha}{2A\sqrt{H_{10}-H_{20}}} + \dfrac{-\alpha}{2A\sqrt{H_{20}-H_{30}}}  &   \dfrac{\alpha}{2A\sqrt{H_{20}-H_{30}}} \\0 &  \dfrac{\alpha}{4A\sqrt{H_{20}-H_{30}}} &  \dfrac{-\alpha}{4A\sqrt{H_{20}-H_{30}}} +  \dfrac{-\alpha}{4A\sqrt{H_{30}}} \end{array}\right)\left(\begin{array}{c}\tilde{H}_1\\  \tilde{H}_2 \\  \tilde{H}_3\end{array}\right) \end{equation} \qquad(3.54)$

Podobnie jak to było w przypadku zlinearyzowanych równań stanu dla obiektu korzystamy z (3.34)-(3.35) i wprowadzamy zmienną $a$ (3.37). Zlinearyzowane równania stanu dla układu regulacji mają teraz postać

$\begin{equation}\left(\begin{array}{c}\dfrac{d\tilde{H}_1}{dt}\\ \dfrac{d\tilde{H}_2}{dt}  \\  \dfrac{d\tilde{H}_3}{dt}\end{array}\right) = \left(\begin{array}{ccc}-2a & 2a & \dfrac{k_p}{A} \\2a &  -4a &  2a \\0 &  a &  -2a\end{array}\right)\left(\begin{array}{c}\tilde{H}_1\\  \tilde{H}_2 \\  \tilde{H}_3\end{array}\right) \end{equation} \qquad(3.55)$

Wielomian charakterystyczny wynosi 

$\begin{eqnarray}W(s) &=& det(sI-A) = det \left(s\left(\begin{array}{ccc}1 & 0 & 0 \\0 &  1 &  0 \\0 &  0 &  1\end{array}\right) - \left(\begin{array}{ccc}-2a & 2a & \dfrac{k_p}{A}  \\2a &  -4a &  2a \\0 &  a &  -2a\end{array} \right) \right)     \\&=& det \left(\left(\begin{array}{ccc}s & 0 & 0 \\0 &  s &  0 \\0 &  0 &  s\end{array}\right) - \left(\begin{array}{ccc}-2a & 2a & \dfrac{k_p}{A}  \\2a &  -4a &  2a \\0 &  a &  -2a\end{array}\right) \right) \qquad(3.56)     \\&=& det \left(\begin{array}{ccc}s+2a & -2a & -\dfrac{k_p}{A}  \\-2a &  s+4a &  -2a \\0 &  -a &  s+2a\end{array}\right) r \\&=& (s+2a)(s+4a)(s+2a) + (-2a)(-2a)\cdot 0 + \left(-\dfrac{k_p}{A}\right) (-2a)(-a)  \\&& - \left(-\dfrac{k_p}{A}\right)  \cdot (s+4a) \cdot 0 - (s+2a)(-2a)(-a) - (-2a)(-2a)(s+2a)  \\&=& (s^2+6as+8a^2)(s+2a) - 2a^2\dfrac{k_p}{A}  - (s+2a)\cdot 2a^2 - 4a^2(s+2a)  \\&=& s^3+8as^2+20a^2s+16a^3 - 2a^2s-4a^3 - 4a^2s - 8a^3 - 2a^2\dfrac{k_p}{A}  \\&=& s^3+8as^2+14a^2s+4a^3 - 2a^2\dfrac{k_p}{A}\end{eqnarray}$

Współczynniki wielomianu charakterystycznego wynoszą

$\begin{equation}a_3 = 1,\ a_2 = 8a,\ a_1 = 14a^2,\ a_0 = 4a^3 - 2a^2\dfrac{k_p}{A}\end{equation} \qquad(3.57)$

Tworzymy teraz macierz Hurwitza dla wielomianu charakterystycznego

$\begin{equation}H = \left(\begin{array}{ccc}a_2 & a_3 & 0 \\a_0 &  a_1 & a_2 \\0 &  0 &  a_0\end{array}\right) = \left(\begin{array}{ccc}8a & 1 & 0 \\4a^3 - 2a^2\dfrac{k_p}{A} &  14a^2 & 8a \\0 &  0 & 4a^3 - 2a^2\dfrac{k_p}{A}\end{array}\right)\end{equation} \qquad(3.58)$

Minory główne macierzy Hurwitza wynoszą

$\begin{equation}|8a|,\ \left|\begin{array}{cc}8a & 1  \\4a^3 - 2a^2\dfrac{k_p}{A} &  14a^2 \end{array}\right|,\ \left|\begin{array}{ccc}8a & 1 & 0 \\4a^3 - 2a^2\dfrac{k_p}{A} &  14a^2 & 8a \\0 &  0 & 4a^3 - 2a^2\dfrac{k_p}{A}\end{array}\right|\end{equation}\qquad(3.59)$

Wykorzystujemy teraz Kryterium Hurwitza do sprawdzenia stabilności punktu pracy układu regulacji

• dla uzyskania stabilności asymptotycznej wszystkie współczynniki wielomianu charakterystycznego muszą być dodatnie

              $\begin{equation}  a_3 = 1>0,\ a_2 = 8a>0,\ a_1 = 14a^2>0,\ a_0 = 4a^3 - 2a^2\dfrac{k_p}{A}>0\end{equation} \qquad(3.60)$

•  dla uzyskania stabilności asymptotycznej wszystkie minory główne macierzy Hurwitza muszą być dodatnie

            $\begin{eqnarray} |8a| &=& 8a >0 \qquad(3.61)\\  \left| \begin{array}{cc}  8a & 1  \\  4a^3 - 2a^2\dfrac{k_p}{A} &  14a^2   \end{array}  \right| &=& 8a\cdot 14a^2 - 1\cdot \left(4a^3 - 2a^2\dfrac{k_p}{A}\right) \\   &=& 112a^3 - 4a^3 +  2a^2\dfrac{k_p}{A}  \\     &=& 108a^3 + 2a^2\dfrac{k_p}{A} > 0 \qquad(3.62)\\    \left|    \begin{array}{ccc}    8a & 1 & 0 \\  4a^3 - 2a^2\dfrac{k_p}{A} &  14a^2 & 8a \\    0 &  0 & 4a^3 - 2a^2\dfrac{k_p}{A}    \end{array}   \right| &=& 8a \cdot 14a^2 \cdot \left(4a^3 - 2a^2\dfrac{k_p}{A}\right)  \qquad(3.63)\\    &&  + 1\cdot 8a \cdot 0 + 0\cdot  \left(4a^3 - 2a^2\dfrac{k_p}{A}\right) \cdot 0 \\    && - 0\cdot 14a^2 \cdot 0 - 8a \cdot 8a \cdot 0   \\   && - 1\cdot \left(4a^3 - 2a^2\dfrac{k_p}{A}\right) \cdot \left(4a^3 - 2a^2\dfrac{k_p}{A}\right)   \\   &=& \left(4a^3 - 2a^2\dfrac{k_p}{A}\right) \left( 8a \cdot 14a^2 - \left(4a^3 - 2a^2\dfrac{k_p}{A}\right) \right) \\  &=& \left(4a^3 - 2a^2\dfrac{k_p}{A}\right) \left(108a^3 + 2a^2\dfrac{k_p}{A}\right)  >0   \end{eqnarray}$

Warunki na stabilność asymptotyczną punktu pracy układu regulacji, zawierające $k_p$, są następujące

$\begin{eqnarray}4a^3 - 2a^2\dfrac{k_p}{A}&>&0 \qquad(3.64) \\108a^3 + 2a^2\dfrac{k_p}{A} &>& 0 \qquad(3.65) \\\left(4a^3 - 2a^2\dfrac{k_p}{A}\right) \left(108a^3 + 2a^2\dfrac{k_p}{A}\right) &>& 0 \qquad(3.66)\end{eqnarray}$

Pozostałe warunki są spełnione ponieważ $a>0$. Zauważmy jeszcze, że jeżeli warunki (3.64) i (3.65) są spełnione, to automatycznie warunek (3.66) też jest spełniony. Obliczmy teraz zakres wartości $k_p$ regulatora, dla których punkt pracy układu regulacji jest stabilny asymptotycznie. Z (3.64) mamy

$\begin{eqnarray}4a^3 - 2a^2\dfrac{k_p}{A} &>& 0\qquad\\ 4a^3 >2a^2\dfrac{k_p}{A}  /\div 2a^2 \qquad\\2a>\dfrac{k_p}{A}  /\cdot A \qquad\\2aA &>& k_p \qquad \\k_p & < & 2aA \qquad(3.67)\end{eqnarray}$

Z (3.65) mamy

$\begin{eqnarray}108a^3 + 2a^2\dfrac{k_p}{A} &>& 0\\ 2a^2\dfrac{k_p}{A} &>& -108a^3 \qquad /\div 2a^2 r\\\dfrac{k_p}{A} &>& -54a \qquad /\cdot A r\\k_p &>& -54aA   \qquad(3.68)\end{eqnarray}$

Ostatecznie, punkt pracy zlinearyzowanego, a także nieliniowego układu regulacji jest stabilny asymptotycznie, jeżeli wzmocnienie regulatora proporcjonalnego mieści się w zakresie

$\begin{equation}-54aA < k_p < 2aA\qquad(3.69)\end{equation}$

Przeanalizujmy teraz powyższy warunek za pomocą symulacji działania układu. Przyjmujemy następujące wartości parametrów obiektu $A = 0.5$, $\alpha = 1$. Wybieramy punkt pracy obiektu $Q_{we0} = 0.5$, $H_{10}=0.75$, $H_{20}=0.5$, $H_{30}=0.25$. Stała $a$ wynosi

$\begin{equation}a = \dfrac{\alpha}{4A\sqrt{H_{30}}} = \dfrac{1}{4\cdot 0.5 \sqrt{0.25}} =1\end{equation} \qquad(3.70)$

Zakres wzmocnień regulatora P, dla których punkt pracy układu regulacji pozostaje stabilny asymptotycznie (3.69) wynosi

$\begin{equation}-27 < k_p < 1\end{equation} \qquad(3.71)$

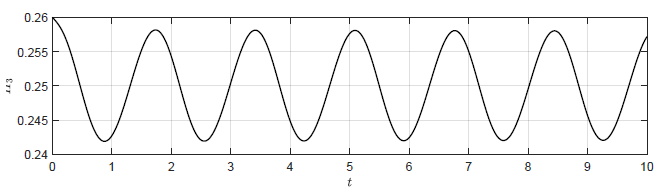
Przeanalizujmy uzyskany przedział $k_p$ zapewniający stabilność asymptotyczną punktu pracy. Większa część przedziału zmienności $k_p$ leży po stronie wartości ujemnych. Jest zgodne z intuicją, ponieważ dla $k_p < 0$ korekta sygnału sterującego ma kierunek, który powoduje zmniejszenie odchyłki regulacji. Ten rezultat pozostaje również w zgodzie z wynikami symulacji (Rys. 2.2-2.5). Sprawdźmy jeszcze, czy $k_p=-27$ wyznacza granicę stabilności układu. Na podstawie Rys. 2.5 mamy, że dla $k_p = -24$ oscylacje sygnału $H_3$ są gasnące (stabilność asymptotyczna), natomiast dla dla $k_p = -32$ oscylacje są narastające (niestabilność). Dla wartości granicznej $k_p=-27$ powinniśmy uzyskać stałe oscylacje. Odpowiedź układu regulacji na niezerowe warunki początkowe $H_1(t_0) =0.76$, $H_2(t_0) =0.51$, $H_3(t_0)=0.26$ dla wzmocnienia regulatora $k_p=-27$ została przedstawiona na Rys. 3.1. Zarówno sygnał wyjściowy $H_{3}(t)$ jak i sygnał sterujący $Q_{we}(t)$ charakteryzują się przebiegiem oscylacyjnym o stałej amplitudzie oscylacji. Warto zauważyć, że na granicy stabilności oscylacje sygnału sterującego i wyjściowego są przesunięte w fazie o 180 stopni. 

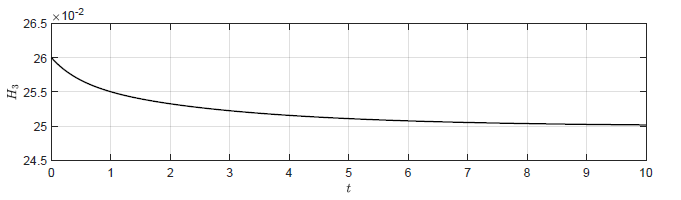
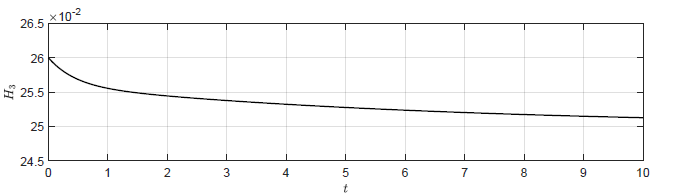
Dla obiektu bez regulatora ($k_p=0$) punkt pracy również jest stabilny asymptotycznie i jest to zgodne z wynikami symulacji (Rys. 2.2(a)). Okazuje się jednak, że także dla niewielkich wartości dodatnich $k_p$ punkt pracy układu regulacji pozostaje stabilny asymptotycznie. Może się to wydawać niezgodne z intuicją, ponieważ dla $k_p > 0$ korekta sygnału sterującego ma kierunek, który powoduje zwiększanie odchyłki regulacji. Układ regulacji traci stabilność dopiero dla odpowiednio dużego dodatniego $k_p$. Zachowanie układu regulacji dla kilku dodatnich wartości $k_p$ została przedstawiona na Rys. 3.2.

a) Trajektoria $H_3(t)$

b) Trajektoria $Q_{we}(t)$

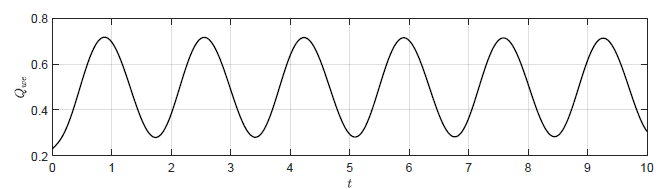
  Rysunek 3.1 Trajektorie $H_3(t)$ orz $Q_{we}$ w układzie regulacji dla $k_p = -27$.

Dodatnia wartość $k_p$ powoduje początkowo wydłużenie czasu regulacji w porównaniu do układu bez regulatora ($k_p=0$). Dla wartości granicznej $k_p=1$ wartość $H_3(t)$ ustala się po pewnym czasie, jednak nigdy nie powraca do wartości z punktu pracy $H_{30} = 0.25$. Dla $k_p>1$ trajektoria $h_3(t)$ stopniowo oddala się od punktu pracy, co świadczy o tym, że punkt pracy układu regulacji jest niestabilny.   

Zajmijmy się teraz badaniem stabilności punktów równowagi wahadła. Równania stanu dla wahadła ze stałym sterowaniem  $M(t) = M_{0}$ (obiekt autonomiczny) mają postać 

$\begin{eqnarray}\dfrac{d\theta(t)}{dt} &=& \omega(t) \qquad(3.72) \\\dfrac{d\omega(t)}{dt} &=& \dfrac{g}{l}sin\theta(t)  - \dfrac{D}{ml^2} \omega(t) +\dfrac{1}{ml^2} M_0 \qquad(3.73)\end{eqnarray}$

Równania punktu równowagi mają postać

$\begin{eqnarray}\omega_0 &=& 0 \qquad(3.74)\\M_0 &=& -mglsin\theta_0 \qquad(3.75)\end{eqnarray}$

Sterowanie w obiekcie zlinearyzowanym jest równe zero

$\begin{equation}\tilde{M} = M(t) - M_0 = M_0 - M_0  = 0\end{equation} \qquad(3.76)$

a) $k_p = 0$

b) $k_p = 0.5$

c) $k_p = 1$

d) $k_p = 1.5$

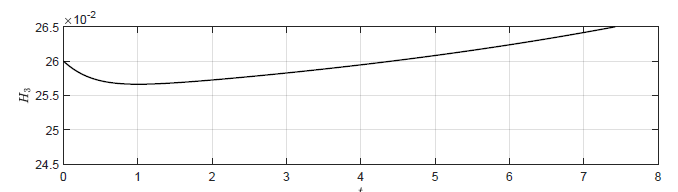
Rysunek 3.2 Trajektorie $H_3(t)$ w układzie regulacji dla różnych wartości wzmocnienia regulatora $k_p$.

Zlinearyzowane równania stanu dla obiektu autonomicznego mają zatem postać 

$\begin{equation}\left(\begin{array}{c}\dfrac{d\tilde{\theta}}{dt}\\ \dfrac{d\tilde{\omega}}{dt}  \end{array}\right) = \left(\begin{array}{cc}0 & 1 \\\dfrac{g}{l}cos\theta_0 &  -\dfrac{D}{ml^2}\end{array}\right)\left(\begin{array}{c}\tilde{\theta}\\ \tilde{\omega}\end{array}\right)  \end{equation} \qquad(3.77)$

Obliczmy wielomian charakterystyczny dla macierzy obiektu zlinearyzowanego

$\begin{equation}A = \left(\begin{array}{cc}0 & 1 \\\dfrac{g}{l}cos\theta_0 &  -\dfrac{D}{ml^2}\end{array}\right)\end{equation}\qquad(3.78)$

Wielomian charakterystyczny wynosi 

$\begin{eqnarray}W(s) &=& det(sI-A) = det \left(s\left(\begin{array}{ccc}1 & 0 \\0 &  1 \end{array}\right) - \left(\begin{array}{cc}0 & 1 \\\dfrac{g}{l}cos\theta_0 &  -\dfrac{D}{ml^2}\end{array}\right) \right)     \nonumber \\&=& det \left(\left(\begin{array}{ccc}s & 0 \\0 &  s \end{array}\right) - \left(\begin{array}{cc}0 & 1 \\\dfrac{g}{l}cos\theta_0 &  -\dfrac{D}{ml^2}\end{array}\right) \right)       \\&=& det \left(\begin{array}{cc}s & -1 \\-\dfrac{g}{l}cos\theta_0 &  s+\dfrac{D}{ml^2}\end{array}\right) \qquad(3.79)\end{eqnarray}$

Wyznacznik macierzy rozmiaru $2\times 2$ może być obliczony z następującego wzoru

$\begin{equation}det \left(\begin{array}{ccc}a_{11} & a_{12} \\a_{21} &  a_{22} \end{array}\right) = a_{11}a_{22} - a_{12}a_{21} \end{equation} \qquad(3.80)$

Mamy zatem 

$\begin{eqnarray}W(s) &=& det(sI-A) = det \left(\begin{array}{cc}s & -1 \\-\dfrac{g}{l}cos\theta_0 &  s+\dfrac{D}{ml^2}\end{array}\right) \\&=& s\left( s+\dfrac{D}{ml^2} \right) - (-1)\left( -\dfrac{g}{l}cos\theta_0 \right) \nonumber \\&=& s^2 + \dfrac{D}{ml^2}s -\dfrac{g}{l}cos\theta_0  \nonumber \end{eqnarray}\qquad(3.81)$

Współczynniki wielomianu charakterystycznego wynoszą

$\begin{equation}a_2 = 1,\ a_1 = \dfrac{D}{ml^2},\ a_0 = -\dfrac{g}{l}cos\theta_0\end{equation} \qquad(3.82)$

Tworzymy teraz macierz Hurwitza dla wielomianu charakterystycznego. Macierz Hurwitza ma rozmiar $2\times 2$ i postać

$\begin{equation}H = \left(\begin{array}{cc}a_1 & a_2 \\0 &  a_0\end{array}\right) = \left(\begin{array}{cc}\dfrac{D}{ml^2} & 1 \\0 &  -\dfrac{g}{l}cos\theta_0\end{array}\right)\end{equation} \qquad(3.83)$

Minory główne macierzy Hurwitza wynoszą

$\begin{equation}\left|\dfrac{D}{ml^2}\right|,\ \left|\begin{array}{cc}\dfrac{D}{ml^2} & 1 \\0 &  -\dfrac{g}{l}cos\theta_0\end{array}\right|\end{equation} \qquad(3.84)$

Wykorzystujemy teraz Kryterium Hurwitza do sprawdzenia stabilności asymptotycznej punktu równowagi wahadła

• współczynniki wielomianu charakterystycznego muszą być dodatnie

              $\begin{equation} a_2 = 1>0,\ a_1 = \dfrac{D}{ml^2}>0,\ a_0 = -\dfrac{g}{l}cos\theta_0 >0 \end{equation} \qquad(3.85)$

• minory główne macierzy Hurwitza muszą być dodatnie

              $\begin{eqnarray} \left|\dfrac{D}{ml^2}\right| &=& \dfrac{D}{ml^2} >0 \qquad(3.86)\\ \left|  \begin{array}{cc} \dfrac{D}{ml^2} & 1 \\ 0 &  -\dfrac{g}{l}cos\theta_0  \end{array}  \right| &=& \dfrac{D}{ml^2}\cdot \left(-\dfrac{g}{l}cos\theta_0\right) - 1\cdot 0 = -\dfrac{D}{ml^2}\cdot \dfrac{g}{l}cos\theta_0  > 0 \qquad(3.87)\end{eqnarray}$

Parametry obiektu $m,g,l,D$ są dodatnie. O spełnieniu nierówności w kryterium Hurwitza decyduje zatem znak wyrażenia $cos\theta_0$. Jeżeli $cos\theta_0 > 0$ (punkt równowagi powyżej położenia horyzontalnego wahadła), to nie wszystkie nierówności w kryterium Hurwitza są spełnione, co oznacza, że taki punkt równowagi jest niestabilny. Jeżeli $cos\theta_0 < 0$ (punkt równowagi poniżej położenia horyzontalnego wahadła), to wszystkie nierówności w kryterium Hurwitza są spełnione, co oznacza, że taki punkt równowagi jest stabilny asymptotycznie. Te wnioski pozostają w zgodzie z wynikami symulacji. Dla punktu równowagi odpowiadającego $\theta_0 = \dfrac{5\pi}{6}$ obiekt przejawiał zachowanie stabilne (Rys. 1.14), podczas, gdy dla punktu równowagi odpowiadającego $\theta_0 = \dfrac{\pi}{6}$ obiekt przejawiał zachowanie niestabilne (Rys. 1.15). 

Zbadajmy teraz stabilność punktu pracy układu regulacji wahadła z regulatorem P. Równania stanu dla układu regulacji mają postać

$\begin{eqnarray}\dfrac{d\theta(t)}{dt} &=& \omega(t) \qquad(3.88)  \\\dfrac{d\omega(t)}{dt} &=& \dfrac{g}{l}sin\theta(t)  - \dfrac{D}{ml^2} \omega(t) +\dfrac{1}{ml^2} \left( k_p (\theta(t)-\theta_0) + M_0  \right) \qquad(3.89)\end{eqnarray}$

Rozważamy punkt pracy określony przez $\theta_0$, $\omega_0$ orz $M_0$. Zlinearyzowane równania stanu (2.61)-(2.62) dla układu regulacji zapisane w postaci macierzowej mają postać

$\begin{equation}\left(\begin{array}{c}\dfrac{d\tilde{\theta}}{dt}\\ \dfrac{d\tilde{\omega}}{dt}  \end{array}\right) = \left(\begin{array}{cc}0 & 1 \\\dfrac{g}{l}cos\theta_0 + \dfrac{1}{ml^2}k_p &  -\dfrac{D}{ml^2}\end{array}\right)\left(\begin{array}{c}\tilde{\theta}\\ \tilde{\omega}\end{array}\right) \end{equation} \qquad(3.90)$

Wielomian charakterystyczny wynosi 

$\begin{eqnarray}W(s) &=& det(sI-A) = det \left(s\left(\begin{array}{ccc}1 & 0 \\0 &  1 \end{array}\right) - \left(\begin{array}{cc}0 & 1 \\\dfrac{g}{l}cos\theta_0 +\dfrac{1}{ml^2}k_p  &  -\dfrac{D}{ml^2}\end{array}\right) \right)     \nonumber \\&=& det \left(\left(\begin{array}{ccc}s & 0 \\0 &  s \end{array}\right) - \left(\begin{array}{cc}0 & 1 \\\dfrac{g}{l}cos\theta_0 +\dfrac{1}{ml^2}k_p &  -\dfrac{D}{ml^2}\end{array}\right) \right)       \\&=& det \left(\begin{array}{cc}s & -1 \\-\dfrac{g}{l}cos\theta_0 -\dfrac{1}{ml^2}k_p &  s+\dfrac{D}{ml^2}\end{array}\right) \nonumber \\&=& s\left( s+\dfrac{D}{ml^2} \right) - (-1)\left( -\dfrac{g}{l}cos\theta_0 -\dfrac{1}{ml^2}k_p\right) \nonumber \\&=& s^2 + \dfrac{D}{ml^2}s -\dfrac{g}{l}cos\theta_0 -\dfrac{1}{ml^2}k_p \nonumber \end{eqnarray}\qquad(3.91)$

Współczynniki wielomianu charakterystycznego wynoszą

$\begin{equation}a_2 = 1,\ a_1 = \dfrac{D}{ml^2},\ a_0 = -\dfrac{g}{l}cos\theta_0 -\dfrac{1}{ml^2}k_p\end{equation} \qquad(3.92)$

Tworzymy teraz macierz Hurwitza dla wielomianu charakterystycznego

$\begin{equation}H = \left(\begin{array}{cc}\dfrac{D}{ml^2} & 1 \\0 &  -\dfrac{g}{l}cos\theta_0 -\dfrac{1}{ml^2}k_p\end{array}\right)\end{equation} \qquad(3.93)$

Minory główne macierzy Hurwitza wynoszą

$\begin{equation}\left|\dfrac{D}{ml^2}\right|,\ \left|\begin{array}{cc}\dfrac{D}{ml^2} & 1 \\0 &  -\dfrac{g}{l}cos\theta_0 -\dfrac{1}{ml^2}k_p\end{array}\right|\end{equation} \qquad(3.94)$

Wykorzystujemy teraz Kryterium Hurwitza do sprawdzenia stabilności asymptotycznej punktu pracy układu regulacji położenia wahadła

• współczynniki wielomianu charakterystycznego muszą być dodatnie

              $\begin{equation} a_2 = 1>0,\ a_1 = \dfrac{D}{ml^2}>0,\ a_0 = -\dfrac{g}{l}cos\theta_0 -\dfrac{1}{ml^2}k_p >0 \qquad(3.95)\end{equation}$ 

• minory główne macierzy Hurwitza muszą być dodatnie

Nierówności w kryterium Hurwitza będą spełnione jeżeli będzie spełniony warunek 

$\begin{eqnarray}-\dfrac{g}{l}cos\theta_0 -\dfrac{1}{ml^2}k_p&>&0  \\-\dfrac{g}{l}cos\theta_0 &>&\dfrac{1}{ml^2}k_p \qquad /\cdot ml^2 \\-mglcos\theta_0 &>&k_p  \\ k_p & < & -mglcos\theta_0 \end{eqnarray}$

Przeanalizujmy teraz powyższy warunek za pomocą symulacji działania układu. Przyjmujemy parametry modelu obiektu $m = 0.1$, $l = 1$, $g = 10$, $D = 0.1$. Wybieramy punkt pracy układu regulacji $\theta_0=\dfrac{\pi}{6}$, $\omega_0=0$,  $M_{0} = -0.5$. Aby punkt pracy układu regulacji był stabilny $k_p$ musi spełniać warunek

$\begin{equation} k_p < -mglcos\theta_0 = -0.1\cdot 10 \cdot 1 \cdot \dfrac{\sqrt{3}}{2} = -\dfrac{\sqrt{3}}{2} \simeq -0.87\end{equation} \qquad(3.98)$

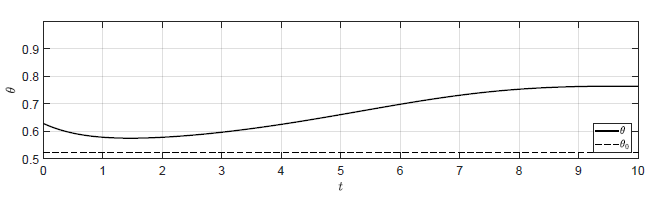
a) $k_p = 0.75$

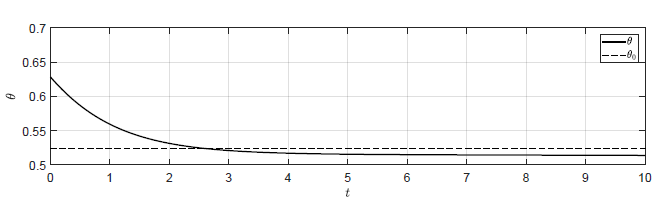
b) $k_p = -0.8$

c) $k_p = -\dfrac{\sqrt{3}}{2}$

d) $k_p = -0.9$

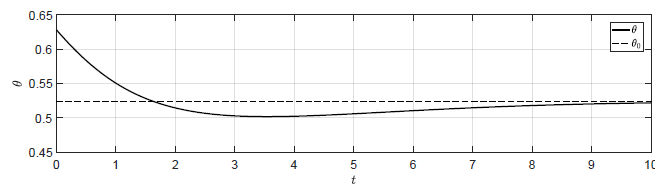
Rysunek 3.3 Trajektorie $\theta(t)$ w układzie regulacji dla różnych wartości wzmocnienia regulatora $k_p$.

Ten warunek pozostaje w zgodzie z wynikami symulacji (Rys. 2.9 i 2.10). Sprawdźmy jeszcze zachowanie układu dla $k_p$ bliskich wartości granicznej. Odpowiedź układu regulacji na warunki początkowe $\theta(t_0) = \dfrac{\pi}{5}$, $\omega(t_0) = -0.1$ dla różnych wartości $k_p$ została przedstawiona na Rys. 3.3. Dla $k_p \geq -\dfrac{\sqrt{3}}{2}$ trajektoria $\theta(t)$ nie powraca do $\theta_0$. Jednak już dla wartości $k_p$ nieco mniejszej od wartości granicznej trajektoria $\theta(t)$ powraca do $\theta_0$.