Podręcznik

Interesuje nas określenie funkcji H opisującej zależność między dwiema wielkościami x i y. Jeżeli wartości wielkości (zmiennych) możemy mierzyć za pomocą fizycznego eksperymentu wiążącego w (uporządkowane) pary liczbowe wartości tych wielkości, znamy ciąg pomiarów \({(x_k, y_k)}\), to mamy do czynienia z tzw. zadaniem identyfikacji modelu funkcji.

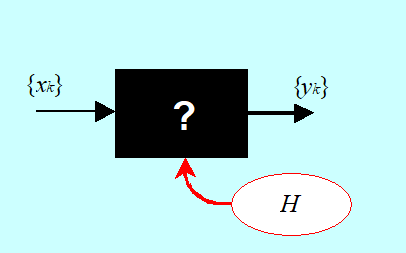
W praktyce rzadko kiedy mamy do czynienia z czarną skrzynką taką jak na rysunku. Często związek łączący zmienne znamy z dokładnością do n-wymiarowego wektora parametrów liczbowych \(\alpha = (\alpha_1,..., \alpha_n)\). Skrzynka jest „szara” i wyznaczyć trzeba konkretną wartość parametrów.

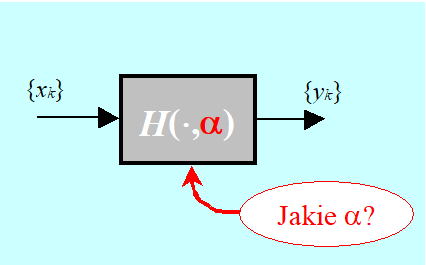
Zapiszmy teraz stosowne zadanie optymalizacji przyjmując, że mamy do czynienia z szarą skrzynką.

Przyjmujemy wiec, że znamy funkcję dwu zmiennych

\(\mathbb{R}\times\mathbb{R}^n∍(x,α)↦H(x,α)∈R\)

(\(\alpha \) jest n-wymiarowym wektorem parametrów), a także ciąg par pomiarów \({(x_k,y_k)}_{k=1}^m.\)

Jeżeli dla każdego (\(\alpha \) zdefiniujemy ciąg różnic między wielkością zmierzoną a przewidywaną przez model

\((\forall\ k\in\overline{1,m})\ r_k(\alpha)=y_k-H(x_k,\alpha),\)

to jako kryterium wyboru „najlepszego (\(\alpha \) ” powinniśmy wybrać funkcję, która te wszystkie różnice będzie minimalizować. Ponieważ dodatnie różnice są tak samo „złe” jak ujemne, to funkcja oceniająca, w najprostszym przypadku, powinna mieć jedną z dwu form

\(\alpha\mapsto\ f^1(\alpha)=\sum_{k=1}^{m}\left|r_k(\alpha)\right|\mathrm{\mathrm{\ \ }albo\ \ }\alpha\mapsto f^2(\alpha)=\sum_{k=1}^{m}\left(r_k(\alpha)\right)^2 ,\)

(proszę porównać przykład poprzedni).

Jak pamiętamy, do ostatecznego sformułowania zadania optymalizacji potrzebne jest określenie zbioru dopuszczalnego. W przypadku zadań identyfikacji czasami nie ma wyraźnych ograniczeń na wartości parametrów. Gdy takie ograniczenia występują zapiszemy je w bardzo ogólny sposób, jako wymaganie \(\alpha \in A\) , gdzie domknięty zbiór \(A \in  \mathbb{R}^n \)jest znany.

Możemy więc sformułować np. następujące zadania minimalizacji (identyfikacji modelu):

• Pierwsze, wymyślone w pierwszej połowie XIX w. przez K. Gaussa: tzw. zadanie doboru parametrów modelu nieliniowego metodą najmniejszych kwadratów

znaleźć \(\alpha^o={\rm argmin}_{\alpha\in\ \mathbb{R}^n}{\sum_{k=1}^{m}\left(y_k-H(x_k,\alpha)\right)^2}.\)

• Drugie

znaleźć \(\alpha^o={\rm argmin}_{\alpha\in\ A}{\sum_{k=1}^{m}\left|y_k-H(x_k,\alpha)\right|}.\)

Zwróćmy tu uwagę na fakt, że zadanie Gaussa sformułowaliśmy jako zadanie bez ograniczeń, a zadanie drugie jako zadanie z ograniczeniami na wartości parametrów. Ponadto w praktyce, podobnie jak w przykładzie dotyczącym projektowania autopilota opisanym w punkcie 2.2, częściej parametry modelu dobiera się metodą najmniejszych kwadratów (funkcja \(f^2\)), bo to zadanie jest łatwiej rozwiązać (nawet gdy dodamy do niego ograniczenia).

Co łączy te trzy przykłady?

W obu, wykorzystując wiedzę i doświadczenie konkretnych nauk danego rodzaju sformalizowano zadanie optymalizacji, inaczej mówiąc zbudowano matematyczny model zadania optymalizacji o tej samej, typowej strukturze.  Przedstawimy teraz ten abstrakcyjny model formalnie.