Podręcznik

Każde sensowne kryterium podziału zbioru pewnych obiektów powinno być konstruowane z myślą o wartości praktycznej takiego podziału. Większość stosowanych klasyfikacji zadań optymalizacji dzieli je na zadania „łatwiejsze” i „trudniejsze”. My też pójdziemy tą drogą. 

Pierwszy podział, to podział podstawowy na

• Zadania bez ograniczeń (wszystkie warianty są dopuszczalne).
• Zadania z ograniczeniami (zadania w których określono zbiór wariantów dopuszczalnych).

Rozwiązać zadanie bez ograniczeń jest prościej niż z ograniczeniami.

Drugi podział to wyróżnienie 

• Zadań liniowych, w których wszystkie funkcje określające zadanie (tzn. funkcje $f, g_j , h_k$) są afiniczne, tzn. są, przy notacji macierzowej, funkcjami postaci

$x\mapsto\ a^Tx+\gamma=\sum_{i=1}^{n}{a_ix_i+\gamma},$

gdzie x jest wektorem kolumnowym, $\alpha^T$ oznacza wektor wierszowy, a $\gamma$ jest liczbą.

• Zadań nieliniowych, w których co najmniej jedna funkcja nie jest afiniczna.

Przy tym podziale mamy pewien kłopot terminologiczny. Dla matematyka funkcja liniowa to funkcja $x\mapsto\ a^Tx,$ przyjmująca wartość zero w zerze. Inżynier najczęściej rozciąga tę nazwę i na funkcje afiniczne.

Zadanie optymalnego planowania produkcji omawiane w punkcie 2.1 jest liniowe i nie jest to przypadek. Wiele zadań optymalizacji, które muszą rozwiązywać menedżerowie daje się zapisać jako zadania liniowe.

Rys.1.7 pokazuje, że funkcje nieliniowe mogą zachowywać się bardzo różnie. Za „najlepiej prowadzące się” funkcje nieliniowe matematycy uważają dwie klasy funkcji: klasę funkcji wypukłych i klasę funkcji gładkich. Dla porządku przypomnę ich definicje.

Pewnego wyjaśnienia wymaga, jakie własności powinna mieć funkcja aby była gładka. Najsłabsze wymaganie, to wymaganie różniczkowalności. Przy czym, intuicyjnie, funkcja mająca pierwszą pochodną ciągłą jest „bardziej gładka” niż funkcja tylko różniczkowalna itd. Pokazuje to Rys. 1.9 ciągłej funkcji sklejonej

$x\mapsto\ f(x)=\left\{\begin{matrix}\ \ \ ax^2\mathrm{\mathrm{\ \ }dla\ }x\geq0\\-ax^2\mathrm{\mathrm{\ }gdy\ przeciwnie}\\\end{matrix}\right., \, \mathrm{dla } \, a > 0.$

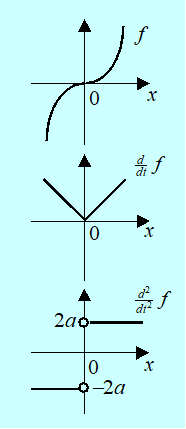
Intuicyjnie jest oczywiste, że zadnia liniowe są prostsze od nieliniowych. 

Trzeci podział to

• Zadania nieróżniczkowalne gdy co najmniej jedna funkcja zadania nie jest różniczkowalna.
• Zadania gładkie klasy Cⁿ , gdzie n jest rzędem ciągłej pochodnej funkcji występującej w zadaniu mającej ją najniższą.

Następny podział związany jest z wypukłością

• Zadania wypukłe gdy funkcja wyboru f i zbiór dopuszczalny D są wypukłe.
• Zadania niewypukłe gdy funkcja f  lub zbiór D nie jest wypukły.

Odpowiedz na pytanie, kiedy zbiór dopuszczalny D określony wzorem (1.9) jest wypukły daje następujący lemat.

Zatem liniowe zadanie optymalizacji jest zadaniem wypukłum.

O zadaniach wyróżnionych przez dwie ostatnie klasyfikacje można powiedzieć, że najdogodniejsze do optymalizacji są zadania co najmniej dwukrotnie różniczkowalne w sposób ciągły i jednocześnie wypukłe.

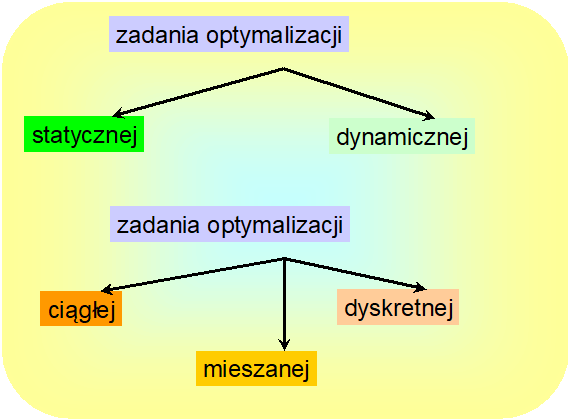
Sformułowana w punkcie 2.4 ogólna postać zadania optymalizacji ZO jest zadaniem tzw. optymalizacji statycznej. Dlaczego statycznej? Porównywane warianty x są charakteryzowane przez wektory o skończonej liczbie współrzędnych (oznaczyliśmy ją przez n) $x\in\ {\mathbb{R}}^n$. Nie porównujemy w nim różnych zachowań określonego obiektu w czasie, a więc różnych funkcji zmiennej, która przyjmuje wartości z pewnego przedziału liczb rzeczywistych. Takie zadania optymalizacji nazywa się zadaniami optymalizacji dynamicznej.

Jednym z najprostszych (w sformułowaniu) zadań optymalizacji dynamicznej jest tzw. zadanie wyznaczenia sterowania czaso-optymalnego. 

Przykład 1.1.
Zadanie wyznaczenia sterowania czaso-optymalnego
Jako przykład takiego zadania rozważmy zagadnienie przesunięcia ciała (wagonika) o masie m z pewnego położenia początkowego x₀ w zadane położenie końcowe x_f za pomocą silnika elektrycznego.

 

Rys. 1.10: Przemieszczający się wagonik

Przyjmijmy, że układ sterowania silnikiem jest taki, że możemy ustalać jego moment obrotowy M. Załóżmy nadto, że tarcie jest pomijalne. Przy takich założeniach zgodnie z Drugą Zasadą Newtona równanie ruchu ciała jest następujące

$(\forall t\geq t_0)m\frac{d^2}{dt^2}e(t)=M(t), \qquad (1.10)$

gdzie oznaczono $(\forall t)e(t)=x_f-x(t)$, a $x(t)$ to położenie w chwili t.
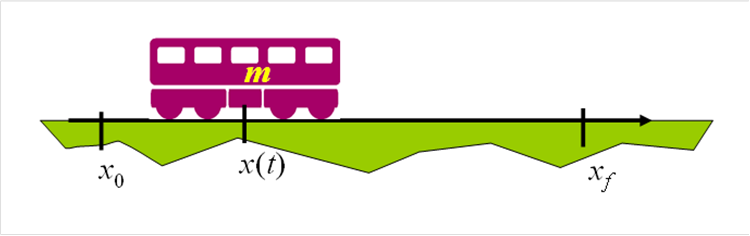
W praktyce moment rozwijany przez silnik nie może przekroczyć pewnej wartości maksymalnej M_max , co daje pierwsze ograniczenie 
$(\forall t\geq t_0)|M(t)|\leq M_{\mathrm{max}}$
czyli nieskończoną i nieprzeliczalną liczbę ograniczeń chwilowych. 
Zauważmy, że zgodnie z przyjętym określeniem w zadaniach optymalizacji statycznej liczba ograniczeń musi być przeliczalna i skończona.
Zadanie wyznaczenia sterowania czaso-optymalnego formułuje się następująco:
znaleźć takie sterowanie (zmiany w czasie momentu) $[t_0,\infty[∍t↦Mo(t)∈R$, które przeprowadzi ciało z położenia początkowego $x_0$ do położenia końcowego $x_f$w jak najkrótszym czasie T^o i ponadto w położeniu końcowym ciało będzie w spoczynku, to znaczy

 $\dfrac{d}{dt}e(t_0+T^o)=0. \qquad (1.11)$

Przemieszczanie ciała może odbywać się tylko zgodnie z równaniem (1.10) – stanowi więc ono trzecie ograniczenie w tym zadaniu. Trzecie, bo drugim jest przedstawione powyżej wymaganie (1.11).
Zadanie wydaje się tak proste, że można próbować je rozwiązać kierując się tylko podstawową znajomością fizyki i zdrowym rozsądkiem.
Ponieważ przyspieszenie wagonika jest ograniczone (nie może być większe niż M_max/m ) to przy założeniu (istotnym), że w chwili początkowej wagonik był w spoczynku:

$\dfrac{de}{dt}(t_0)=0,\,\dfrac{d^2e}{dt^2}(t_0-)=0,$

drogę $x_f  – x_0$ przejedzie w najkrótszym czasie jeżeli do jej połowy, punktu $(x_f – x_0)/2$, będzie poruszał się z maksymalnym dopuszczalnym przyspieszeniem M_max /m a w jej drugiej części — z maksymalnym hamowaniem  –M_max /m

 

Rys. 1.11: Rozwiązanie Zadania wyznaczenie sterowania czaso-optymalnego

Zdrowy rozsądek jednak nas tu trochę zawodzi, bo sterowania (zmiany momentu) przestawiającego się momentalnie z wartości M_max na –M_max nie jesteśmy w stanie zrealizować – zadanie nie ma rozwiązania, jeżeli poszukujemy go w zbiorze funkcji realizowalnych technicznie – zbiorze funkcji ciągłych.
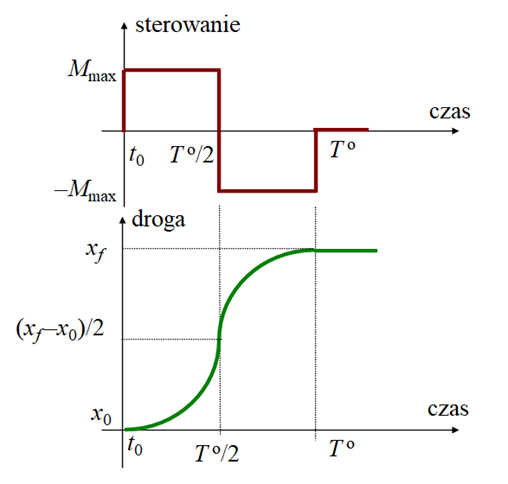
Pojawia się tu istotny problem tego typu zadań: w zbiorze jakich funkcji szukamy rozwiązań? 
Z matematycznego punktu widzenia nie jest to trudne pytanie – funkcje które mogą zawierać skokowe zmiany, to tzw. funkcje przedziałami ciągłe.

 

Rys. 1.12: Przykład funkcji przedziałami ciągłej, funkcja $1(t)$

Zadanie ma więc rozwiązanie matematyczne, ale w praktyce jest ono nieosiągalne i trzeba posługiwać się stosownymi przybliżeniami takich funkcji, co jest skomplikowane.
Ze względu na złożoność nie będziemy analizowali dalej problemów związanych z techniczną realizacją przybliżenia sterowania optymalnego wyznaczonego w tym zadaniu.

Przykład 1.1 przedstawił podstawowe różnice między zadaniami optymalizacji statycznej i dynamicznej, w tych ostatnich

• Szukamy funkcji czasu a nie wektorów liczbowych. Nasze rozważania przenoszą się z przestrzeni $\mathbb{R}^n\$ w dużo bardziej skomplikowane przestrzenie funkcyjne.
• Ograniczeniem jest (wektorowe) równanie różniczkowe.
• Może występować nieprzeliczalna liczba ograniczeń chwilowych.
• Często występuje wymaganie określonego zachowania rozwiązania równania różniczkowego w konkretnej chwili czasu, np. wymaganie podobne do (1.11).

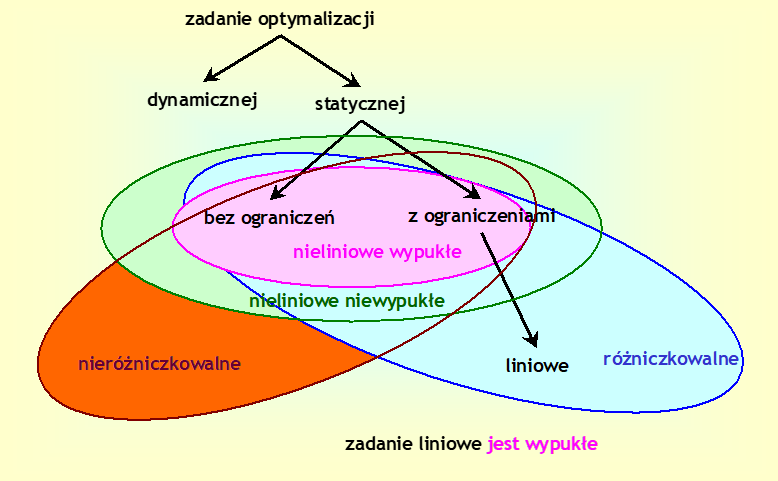
Na poniższym rysunku podsumowujemy nasze dotychczasowe rozważania klasyfikacyjne.

Od funkcji gj oraz hk określających zbiór dopuszczalny w definicji ogólnego zadania optymalizacji ZO nic nie wymagamy – mogą być dowolne. 

Rozważmy zatem zbiór dopuszczalny określony następująco

$D = {(x_1, x_2) | sin(\pi x_1) = 0 \wedge sin(\pi x_2) = 0}.$

Jego obraz jest następujący.

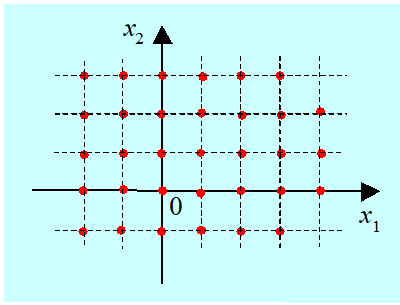
Jest to nieskończony, przeliczalny zbiór izolowanych punktów płaszczyzny, a warianty są opisywane wektorami całkowitoliczbowymi. Zbiory tego typu często nazywa się zbiorami dyskretnymi.

W związku z tym możemy jeszcze wyróżnić:

• Zadania (statycznej) optymalizacji dyskretnej (w liczbach całkowitych).
• Zadania optymalizacji (statycznej) (bez dodatkowego określenia, co oznacza, że z tym terminem związany jest zbiór dopuszczalny wektorów, których składowe mogą przyjmować dowolne wartości rzeczywiste).

Przedstawiony powyżej przykład ograniczeń definiujących zbiór całkowitoliczbowy jest przykładem teoretycznym i ma głownie na celu pokazanie bogactwa „różnorodności” jakie kryje w sobie przyjęte, pozornie proste, określenie zbioru dopuszczalnego. Teraz przedstawię przykład praktycznego zadania optymalizacji dyskretnej, zadania które musi rozwiązać kierownictwo koncernu planującego budowę nowych zakładów produkcyjnych.

 Przykład 1.2.

 Zadanie lokalizacji
Pewien koncern zamierza znacznie powiększyć udział jednego ze swoich niepodzielnych produktów (niepodzielny produkt to np. lodówka, lub lokówka, a także paleta z kubeczkami jogurtu) w rynku i w tym celu planuje wybudowanie szeregu zakładów produkcyjnych go wytwarzających. Menedżerowie koncernu chcą podjąć decyzję minimalizującą łączne koszty lokalizacji i transportu produktu. Przyjmijmy, że rozważnych jest I miejsc lokalizacji. Niech indeksem lokalizacji będzie I, zatem $i\in\overline{1,n}$. Możliwości produkcyjne zakładu zlokalizowanego w miejscu i oznaczymy przez Si a koszt uruchomienia w nim produkcji (dla uproszczenia niezależny od wielkości produkcji) – przez $\gamma _i$ .

Rys. 1.15a): Zakłady produkcyjne

Produkt ma być dostarczany do m miejsc indeksowanych przez I, tu $j\in\overline{1,m}$. Przyjmujemy, że do każdego miejsca odbioru trzeba dostarczyć co najmniej D_j sztuk produktu. Dalej, niech c_ij oznacza koszt wytworzenia i transportu sztuki produktu z lokalizacji i do miejsca odbioru j. Koncern musi też ponieść, niezależne od wielkości przewozu koszty uruchomienia i eksploatacji trasy przewozowe $i \mapsto j$, oznaczymy je $\gamma_{ij}$ .  Na koniec, niech $x_{ij}$ oznacza ilość sztuk produktu przewożonego trasą $i \mapsto j$.
 

Rys. 1.15b): Zadanie lokalizacji

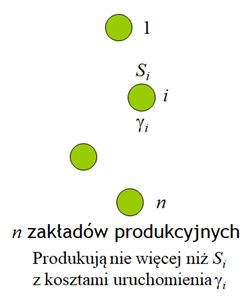
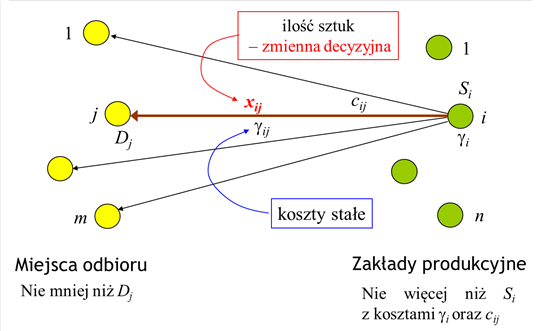
W matematycznym sformułowaniu zadania optymalizacji musimy uwzględnić jeszcze dwa fakty: 

• nie jest oczywiste, że trzeba wybudować nowe fabryki we wszystkich miejscach – trzeba wybrać te miejsca, które dadzą w sumie minimalny koszt uruchomienia produkcji i transportu;
• przewożenie produktu z danego zakładu do wszystkich miejsc odbioru może być zbyt kosztowne, trzeba wybrać właściwą strukturę połączeń między dostawcami a odbiorcami.

Wymagania powyższe uwzględnimy wprowadzając dwie grupy zmiennych o wartościach zero-jedynkowych:

$y_{i}=\left\{\begin{matrix} 1,\,\mathrm{gdy\,miejsce}\,i\,\mathrm{zostalo\,wybrane} \\0,\,\mathrm{w\,przeciwnym\,przypadku} \\\end{matrix}\right.,i\in \overline{1,n}$

$v_{ij}=\left\{\begin{matrix} 1,\,\mathrm{gdy\,trasa}\,i\to j\,\mathrm{jest\,wykorzystywana} \\0,\,\mathrm{w\,przeciwnym\,przypadku} \\\end{matrix}\right.,(i,j)\in \overline{1,n}\times \overline{1,m}$

Przy takim określeniu zmiennych, funkcja kosztów jest następująca

$((x_{ij}),(y_i),(v_{ij}))\mapsto K((x_{ij}),(y_i),(v_{ij}))=\sum_{i=1}^{n}{\gamma_iy_i+\sum_{i=1}^{n}\sum_{j=1}^{m}{c_{ij}x_{ij}+}}\sum_{i=1}^{n}\sum_{j=1}^{m}{\gamma_{ij}v_{ij}}.$

Jest to funkcja $n\cdot m + n +n\cdot m = n(2m + 1)$ zmiennych. Przy czterech miejscach lokalizacji, n = 4, i dwudziestu pięciu odbiorcach, m = 25, daje to 204 zmienne. W porównaniu do zadań optymalizacji, które naprawdę są rozwiązywane przy wspomaganiu decyzji podejmowanych przez menedżerów różnych korporacji, gdzie zmiennych potrafi być kilkanaście tysięcy (np. dlatego, bo trzeba uwzględnić różne produkty a także różne ich rodzaje – całe bogactwo różnych jogurtów), jest to niewiele.
Oczywiste nierówności określające zbiór dopuszczalny są następujące:

• wynikające z ograniczeń możliwości produkcyjnych i-tego zakładu

$(\forall i\in\overline{1,n})\sum_{j=1}^{m}{x_{ij}-S_iy_i\le0}, \qquad (1.12)$

• nieujemności wielkości przewozu (tylko z miejsca i do miejsca j)

$(\forall(i,j)\in\overline{1,n}\times\overline{1,m}) x_{ij}\geq0. \qquad (1.13)$

wynikające z konieczności spełnienia minimalnego zapotrzebowania na produkt w każdym miejscu odbioru

$(\forall j\in\overline{1,m}) D_j-\sum_{i=1}^{n}{x_{ij}\le0}, \qquad (1.14)$

Ograniczenia (1.14) mogliśmy zapisać w takiej postaci, bo jeżeli w miejscu i nie zostanie wybudowana nowa fabryka to, y_i = 0, zatem na mocy (1.12) i (1.13), dla każdego $j\in\overline{1,m}$ wielkość przewozu x_ij = 0.
Przedstawione trzy grupy nierówności nie opisują wszystkich ograniczeń, ponieważ nie są w nich uwzględnione następujące związki logiczne między x_ij (ilością sztuk produktu przewożonego trasą $i \mapsto j$ )a v_ij (zmienną binarną określającą czy trasa $i \mapsto j)$ jest wykorzystywana):

$(\forall i,j)[x_{ij}>0\Rightarrow v_{ij}=1] \qquad (1.15)$

(jeżeli między miejscem i a j jest transportowany produkt, to trzeba ponieść koszty $\gamma_{ij }$), oraz

$(\forall i,j)[v_{ij}=1\Rightarrow x_{ij}>0] \qquad (1.16)$

(jeżeli ponosimy koszty $\gamma_{ij }$  na trasie między i a j, to musimy coś nią przewozić).

Związki te w obowiązujący dla sformułowania zadania optymalizacji „schemat nierówności” można włożyć następująco. 
Zauważmy, że $(\forall i,j)[x_{ij}>0\Rightarrow v_{ij}=1]≡(∀i,j)[vij=0⇒xij=0]$, bo mamy ograniczenie (1.13).
Dla każdej pary $(i, j)$oznaczamy $L-{ij} = min{Si ,Dj }.$ Wprowadźmy ograniczenie

$(\forall(i,j)\in\overline{1,n}\times\overline{1,m}) x_{ij}-L_{ij}v_{ij}\le0. \qquad (1.17)$

Jeśli $v_{ij} = 0$ to z (1.13) i (1.17) wynika, że $x_{ij} = 0$. 
Zatem wprowadzenie ograniczenia (1.17) oznacza uwzględnienie wymagania logicznego (1.15).
Zauważmy teraz, że w punkcie minimalizującym $((x_{ij}^o),(v_{ij}^o))$ mamy

$(\forall x_{ij}^o=0)v_{ij}^o=0. \qquad(1.18)$

Wynika to z faktu, że minimalizujemy sumę po i sum po j, wyrażeń  następujących  $c_{ij}x_{ij}+\gamma_{ij}v_{ij}$,  co dla $vij \in {0,1}$ oznacza, że w punkcie optymalnym musi być spełniony warunek (1.18).
Spełnienie w punkcie minimalizującym tego warunku zwalnia nas z konieczności uwzględnienia warunku (1.16) jako równoważnego z warunkiem

$(\forall i,j)[x_{ij}=0\Rightarrow v_{ij}=0].$

Mamy już „komplet ograniczeń” i wyrażenie określające zbiór dopuszczalny możemy zapisać następująco
$D={((x_{ij}),(y_i),(v_{ij}))\in\mathbb{Z}^{n(2m+1)}|(\forall i\in\overline{1,n})y_i\in{0,1}\land(\forall(i,j)\in\overline{1,n}\times\overline{1,m})v_{ij}\in{0,1}\land(1.12)\land(1.13)\land(1.14)\land(1.17)},$
gdzie przez ℤ (die Zahlen – liczby) oznaczono zbiór liczb całkowitych tj. zbiór {...,–1,0,1,2,...}.
Dla porządku zapiszmy jeszcze zadanie, które trzeba rozwiązać.
Zadanie lokalizacji fabryk z uwzględnieniem kosztów uruchomienia produkcji i transportu

znaleźć  $((x_{ij}^o),(y_i^o),(v_{ij}^o))={\rm argmin}_{((x_{ij}),(y_i),(v_{ij}))\in D}{K}((x_{ij}),(y_i),(v_{ij})).$

Kończąc omawianie przykładu, przedstawmy dwa spostrzeżenia

• określony powyżej zbiór dopuszczalny D przy niewłaściwym doborze parametrów S_i i D_j może być pusty – jest tak gdy suma maksymalnych mocy produkcyjnych jest mniejsza od sumy minimalnych zapotrzebowań.
• sformułowane powyżej zadanie jest zadaniem tzw. liniowej optymalizacji dyskretnej.

 Po wyjaśnieniach przykładu, możemy podać formalną definicję zadania optymalizacji dyskretnej.

Rozważaliśmy zadania optymalizacji, w których zmiennymi są wektory liczb rzeczywistych, jak mówimy zmienne są ciągłe oraz dyskretne zadania optymalizacji, gdzie zmienne to wektory całkowitoliczbowe (zmienne dyskretne). Mogą więc być zadania mieszane, w których część zmiennych jest ciągła, a pozostała – dyskretna. 

Przedstawione dotąd rozważania pokazały, że analizując zadania optymalizacji, obok zwrócenia uwagi na stopień trudności znajdowania ich rozwiązania („łatwiejsze – trudniejsze”, czyli: bez ograniczeń – z ograniczeniami, liniowe – nieliniowe itp.) trzeba także zwrócić uwagę na ich strukturę, co prowadzi do klasyfikacji takiej jak na ostatnim rysunku tego rozdziału.

Wyposażeni w przedstawiony zestaw definicji możemy teraz precyzyjniej określić zakres tego podręcznika. Zajmować się w nim będziemy podstawowymi własnościami zadań (statycznej) optymalizacji (ciągłej) to jest zadań ZO a także poznamy algorytmy służące do rozwiązywania takich zadań.