Podręcznik

Istotnym elementem przedstawionego w poprzednim rozdziale podstawowego algorytmu kierunków poprawy jest zadanie poprawy w kierunku. Wprowadźmy dokładne określenie.

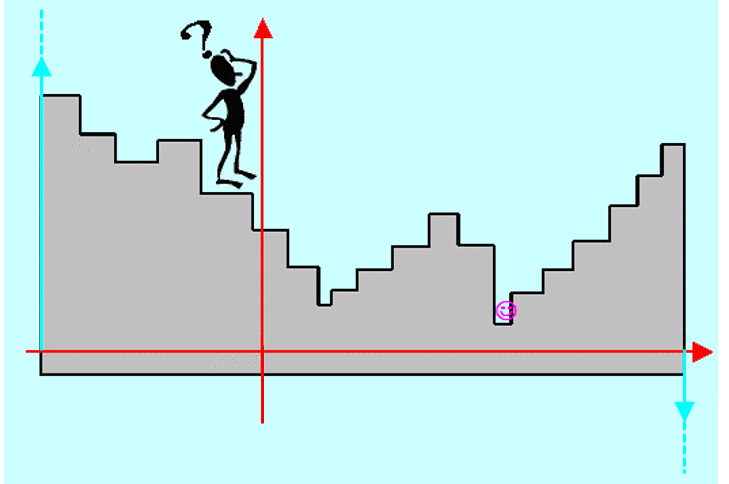
Określenie sposobu znalezienia rozwiązania zadania poprawy w kierunku, to przypominając rozważania punktu 1.4 Modułu pierwszego, pomoc dla Algorytmu, który stoi na schodach i nie bardzo wie jak szybko znaleźć dostatecznie nisko położony stopień, Dla zadania minimalizacji w kierunku to pomoc w jak najszybszym dotarciu na najniższy stopień. W obu przypadkach naturalne postępowanie to metoda prób i błędów (najpierw w prawo, gdy niżej to dalej w prawo, gdy teraz wyżej to w lewo,...), ale nie bardzo wiadomo jak daleko się ruszać (skakać) w kolejnym kroku. 

Posługując się rysunkami poziomicowymi przedstawmy podstawowe problemy z jakimi możemy się spotkać. Zwróćmy uwagę na fakt, że rozważania będą ogólne, ponieważ jest dość oczywiste, że napisanie wzoru dla funkcji dwu zmiennych o poziomicach naszkicowanych na rysunkach to tylko kwestia chęci i czasu.

Przyjmijmy, że kierunki poprawy to kierunki antygradientu  i algorytm doszedł do punktu $x^{(k)}$, w którym wyznaczył kierunek poprawy $d^{(k)}$– Rys. 4.2. 

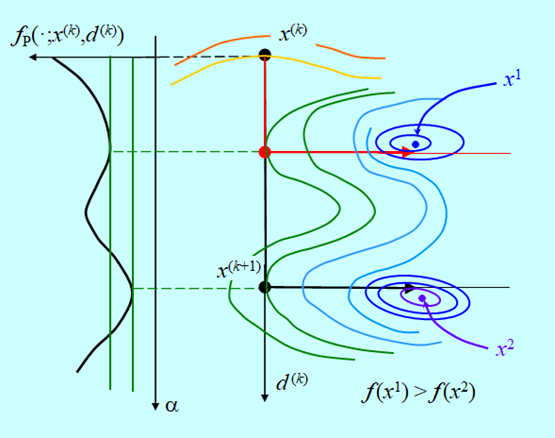
Rysunek powyższy pokazuje sytuację, w której dokładna minimalizacja w kierunku „przeskoczy” lokalne minimum funkcji $f_P (⋅;x^{(k)},d^{(k)})$ i da punkt $x^{(k+1)}$. Kierunek poprawy „wystawiony” w tym punkcie zaprowadzi do minimum globalnego funkcji f. Gdyby skończyć poszukiwanie minimum w kierunku we wcześniej napotkanym minimum lokalnym funkcji $f_P$, to kierunek poprawy zaprowadzi do minimum lokalnego funkcji f. 

Dokładna minimalizacja w kierunku pozwala znaleźć rozwiązanie zadania minimalizacji. Ale przecież nietrudno jest nieco zmodyfikować sytuację. Co się stanie gdy mamy sytuację taką jak na Rys. 4.3?

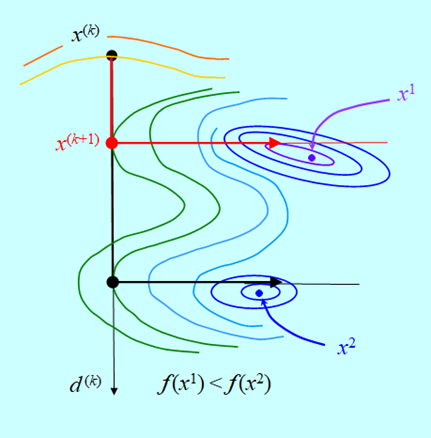
Teraz, „zatrzymanie” minimalizacji w kierunku w punkcie minimum lokalnego funkcji $f_P$ daje dobry rezultat, a dokładna minimalizacja tej funkcji „wpycha” algorytm w obszar przyciągania minimum lokalnego funkcji f.

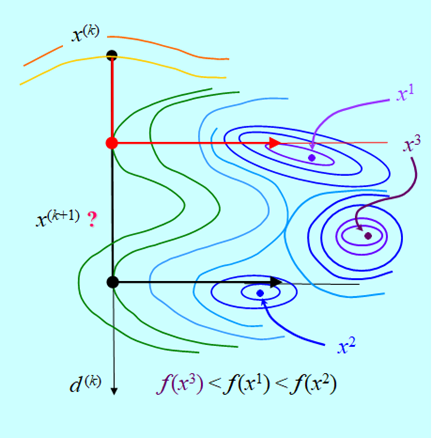
Ten rysunek pokazuje niestety, że algorytm kierunków poprawy przy dokładnej i nie dokładnej minimalizacji w kierunku może „wpaść” w obszar przyciągania któregoś z minimów lokalnych i w konsekwencji nigdy nie znaleźć rozwiązania zadania minimalizacji.

Jakie wnioski należy wyciągnąć z tej analizy.

• Bez dodatkowych założeń o funkcji minimalizowanej albo dodatkowych zabezpieczeń, algorytm kierunków poprawy może znaleźć tylko minimum lokalne.

• Dokładna minimalizacja w kierunku nie zawsze jest potrzebna, a czasem (Rys. 4.4) jest wręcz szkodliwa. Ważne jest aby poprawić funkcję celu w dostateczny sposób, tzn. aby różnica $f(x^{(k)}) – f (x^{(k)} + \alpha ^{(k)}d^{(k)})$ była dodatnia i nie za mała (formalne określa ją współczynnik 𝜗 wprowadzony w definicji zadania ZPK).

Zagadnieniem określenia warunków jakie musi spełniać poprawa aby wystarczyło to do zbieżności algorytmów zaczęto się zajmować na początku lat sześćdziesiątych XX w. Mniej więcej w ich połowie udowodniono dla gładkich funkcji celu twierdzenia pokazujące, że dla szerokiej klasy sposobów generowania kierunków poprawy można zapewnić zbieżność algorytmów do punktu stacjonarnego gradientu bez konieczności dokładnej minimalizacji w kierunku (rozwiązywania zadania ZK), pod warunkiem, że algorytm wyznaczania $\alpha {(k)}$ zapewnia uniknięcie zbyt długich kroków. Wszystkie metody, które będą przedstawione w punkcie następnym są metodami tej klasy.

Przedstawimy teraz warunek, który jest najczęściej stosowany. Jest to tak zwana reguła L. Armijo .

Występujący w powyższej nierówności wektor $d^{(k)}$ jest kierunkiem poprawy w punkcie $x^{(k)}$, zatem zgodnie z definicją $∇f(x^{(k)})d^{(k)}$. Ponieważ $\alpha^{(k)}$ i $\eta$ są większe od zera, to

Wobec tego, przy założeniu że funkcja f ma minimum, z Lematu 3.3 wynika, że 

Powyższa nierówność pozwala na przedstawienie oczywistej graficznej interpretacji reguły Armijo. 

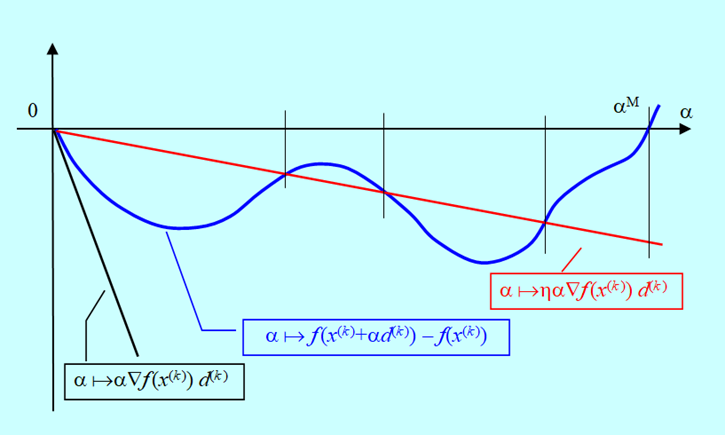
W oparciu o tę regułę można podać następujący, prosty algorytm wyznaczania długości kroku w kierunku, przy założeniu, że potrafimy obliczyć gradient.

Algorytm wyznaczania długości kroku w kierunku oparty na regule Armijo (backtracking line search)

Inicjalizacja

Wybierz początkową długość kroku $s > 0$.

Wybierz parametry algorytmu $\eta$ i $\beta$ (doświadczenie podpowiada $\eta \in [10–5,0.1] oraz \beta \in [0.1,0.5])$

Podstaw i := 0.

Kroki algorytmu

1. Sprawdź nierówność  $f(x^{(k)}+β^i sd^{(k)})-f(x^{(k)})≤ηβ^i s∇f(x^{(k)})d^{(k)}$. ($β^i$ to $β$ do potęgi i). Jeżeli spełniona, podstaw $α^{(k)}:=β^i s$ i stop. Jeśli nie przejdź do 2.
2. Podstaw $i := i + 1$, przejdź do 1.

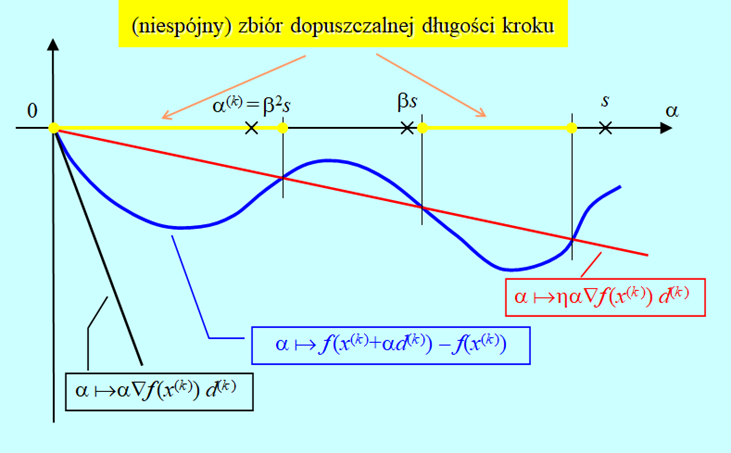
Rys. 4.6 pokazuje, że algorytm wyznaczy $\alpha^{(k)}$ w skończonej ilości kroków (dowód formalny opuszczamy), oraz że wielkość otrzymanego zmalenia funkcji celu zależy w sposób istotny od początkowej długości kroku s.

Algorytm oparty na regule Armijo wyznacza długość kroku w kilku iteracjach. Jest to istotna zaleta w sytuacji, gdy obliczenia wartości funkcji celu są, jak się to często mówi, kosztowne, tzn. zajmują dużo czasu.

Jednak w niektórych przypadkach pożądana jest dobra aproksymacja minimum w kierunku. Algorytmem, który daje taką dobrą aproksymację jest tzw. algorytm złotego podziału, który dla tzw. funkcji unimodalnych  pozwala zlokalizować minimum z dowolną dokładnością. 

Algorytm złotego podziału

Inicjalizacja

Wybierz początkową długość kroku $m > 0$.

Wybierz dokładność lokalizacji minimum $\varepsilon  > 0$.

Kroki algorytmu

1. Oblicz $f(x^{(k)}+md^{(k)})$.
2. Jeżeli $f(x^{(k)}+md^{(k)})≥f(x^{(k)})$ podstaw $a_0 := 0, b_0 := m$ i idź do 5. Jeśli nie, podstaw $j := 0$ i$\alpha_j := 0$, a następnie przejdź do 3.
3. Podstaw $\alpha_j +1 := \alpha_j + m$ i oblicz $f(x^{(k)}+α_{j+1} d^{(k)}).$
4. Jeżeli $f(x^{(k)}+α_{j+}) d^{(k)})≥f(x^{(k)}+α_j d^{(k)})$ podstaw $a_0:= \alpha_{j –1}, b_0 := \alpha_{j +1}$ i idź do 5. Jeśli nie, podstaw $j := j +1$ i idź do 3.
5. Podstaw $i := 0$.
6. Podstaw $l_i := b_i – a_i$.
7. Jeżeli $l_i \leq \varepsilon$ idź do 10. Jeżeli nie, idź do 8.
8. Podstaw $v_i:=a_i+\dfrac{1}{2}(3-√5)l_i$ oraz $w_i:=a_i+\dfrac{1}{2}(√5-1)l_i.$ Oblicz $f(x^{(k)}+v_i d^{(k)})$ oraz $f(x^{(k)}+w_i d^{(k)})$.
9. Jeżeli $f(x^{(k)}+v_i d^{(k)}) < f(x^{(k)}+w_i d^{(k)})$., podstaw $a_{i+1}:= a_i, b_{i+1} := w_i$ , podstaw $i := i+1$ i idź do 6. Jeśli nie, podstaw $a_{i+1}:= v_i, b_{i+1} := b_i$ , podstaw $i := i+1$ i idź do 6.
10. Przyjmij za rozwiązanie $\alpha^{(k)} := \dfrac{1}{2}(a_i +b_i)$ i stop.

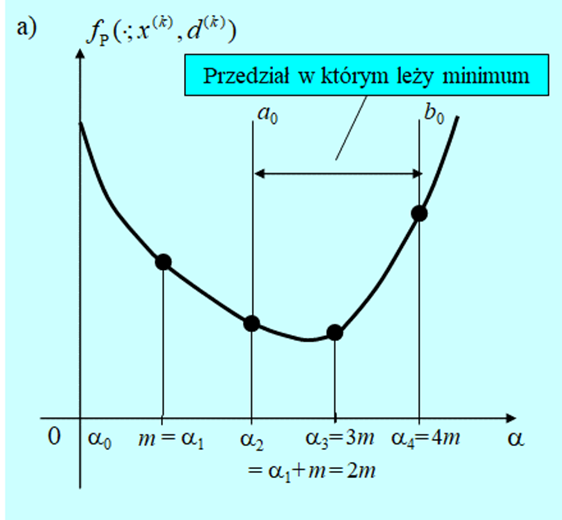
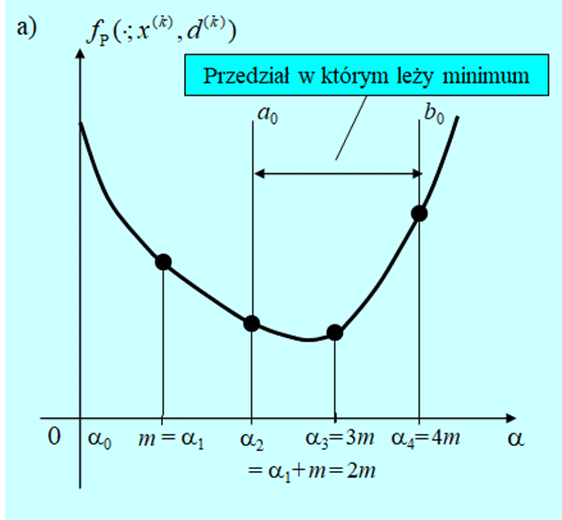
Pierwsze cztery kroki przedstawionego algorytmu to lokalizacja przedziału w którym powinien znajdować się punkt minimalizujący. Jeżeli funkcja $f_P (⋅;x^{(k)},d^{(k)})$ jest unimodalna dla każdego $\alpha >0$, to taki przedział na pewno zostanie znaleziony. Natomiast gdy funkcja minimalizowana nie jest unimodalna to w ten sposób zostanie zlokalizowane jej minimum lokalne.

Następne kroki to symetryczna redukcja przedziału $[a_0, b_0]$ do przedziału o długości mniejszej niż zadana dokładność $\varepsilon$, i wybór jako rozwiązania średniej arytmetycznej z wartości końców tego przedziału (stosujemy tu heurystyczną regułę postępowania: jak nie wiemy gdzie punkt leży, to przyjmujemy, że w środku przedziału).

Nazwa metody wzięła się stąd, że konstruując ten algorytm dla zachowania symetrii posłużono się znanymi już starożytnym zasadami złotego podziału odcinka, które dały niewymierne mnożniki użyte w kroku 8. Zauważmy, że jedną z własności ciągu przedziałów generowanych przez ten algorytm jest stałość stosunku długości podprzedziału usuwanego do aktualnej długości przedziału poszukiwań. Ponieważ nie wiemy, który przedział będzie usunięty, to przy naszych oznaczeniach jest to warunek

$\dfrac{v_k-a_k}{b_k-a_k }=\dfrac{b_k-w_k}{b_k-a_k }=const=\dfrac{1}{2}(3-√5).$

Doświadczenia zebrane w ciągu ponad półwiecza stosowania algorytmu złotego podziału potwierdziły jego przydatność jako metody rozwiązywania zadania minimalizacji w kierunku. Jest to więc wspaniała, w zasadzie heurystyczna, odpowiedź na pytanie męczące nasz Algorytm stojący na schodach na Rys. 4.1.

Innym algorytmem, który jest stosowany w sytuacji gdy uważamy, że trzeba posłużyć się algorytmem dokładniejszym niż algorytm oparty na regule Armijo jest procedura wykorzystująca (kwadratowy) wielomian interpolacyjny Lagrange’a opisana np. w podręczniku A. Stachurski: Wprowadzenie do optymalizacji, Oficyna Wydawnicza PW 2009, podrozdział 3.6. 

Intuicyjnie oczywistym założeniem potrzebnym do poprawnego działania algorytmu złotego podziału (podobnie jak i algorytmu interpolacji kwadratowej), jest wymaganie unimodalności funkcji minimalizowanej w kierunku $f_P (⋅;x^{(k)},d^{(k)})$. Ponieważ przeważnie nie wiemy, czy funkcje, z którymi mamy do czynienia spełniają ten warunek, praktyczne implementacje algorytmów tego typu są wyposażane, tak jak przedstawiony algorytm złotego podziału, w fazę pierwszą która ma doprowadzić (cały czas jesteśmy optymistami) do określenia przedziału unimodalności funkcji $f_ P$.

• Bez dodatkowych założeń o funkcji minimalizowanej albo dodatkowych zabezpieczeń algorytm kierunków poprawy może znaleźć tylko minimum lokalne.
• Zadanie poprawy rozwiązywane w każdym kroku metody kierunków poprawy nie musi być zadaniem minimalizacji. Ważne jest aby poprawić funkcję celu, tzn. aby różnica

• Jeżeli rezygnujemy z minimalizacji w kierunku (rozwiązywane zadanie poprawy nie jest zadaniem minimalizacji w kierunku), to algorytm wyznaczania długości kroku musi dawać krok spełniający pewne warunki, np. regułę Armijo.