Podręcznik

Omówiliśmy realizację pierwszego z zaproponowanych podejść wzbogacenia algorytmu gradientu prostego w pamięć, a polegającego na dodaniu poprawki zależnej od historii. Teraz przyszedł czas na zapoznanie się z drugim podejściem, w którym przeskalowujemy gradient za pomocą macierzy transformacji, w stosowny sposób „zależnej od historii”. Przy tym podejściu krok wykonujemy w kierunku

$d^ {(k)}=-\mathfrak{D} (x^ {(k)},x^((k-1)),...)∇^T f(x^ {(k)})$.

Jak więc dobrze określić zależność macierzy transformacji od bieżącej i przeszłej informacji? 

W punkcie piątym Procedury redukcji zadania optymalizacji bez ograniczeń przedstawionej w punkcie 3.1.1 Modułu trzeciego napisałem: 

„Elementy zbioru rozwiązań równania

$∇f(x ̄)=0.$

traktujemy jako „podejrzanych”, których „sprawdzamy na optymalność” tzn. wyliczamy zbiór ${f(x ̄^j)}$ wartości funkcji f , a następnie typujemy jako kandydata na rozwiązanie wektor dla którego wartość funkcji jest najmniejsza (tylko kandydata na, a nie rozwiązanie, bo Twierdzenie 3.4 jest warunkiem koniecznym!).”

Podane twierdzenia o zbieżności algorytmów gradientu prostego i sprzężonego (Twierdzenia 4.1 i 4.1GS) mówią, że algorytmy te de facto rozwiązują to równanie, co jest jeszcze podkreślone przez użyte w nich kryterium stopu: $||∇f(x^ {(k)})||$ Wobec tego do poszukiwania rozwiązania zadania optymalizacji możemy zastosować zaproponowaną w 1669 roku przez I. Newtona metodę stycznych (w dziele De Analysi per Aequationes Numeri Terminorum Infinitas, w XVII w. nawet Anglicy pisali traktaty naukowe po łacinie). Zapiszmy ją dla naszego zadania polegającego na szukaniu rozwiązania równania

    $F(x)=0,$  gdzie

$\mathbb{R}^n∍x↦F(x)=∇^T f(x)∈\mathbb{R}^n.$

Algorytm zaproponowany przez Newtona jest następujący:

wybierz punkt początkowy $x^{(0)}$, kolejne przybliżenia obliczaj według wzoru

$x^ {(k+1)}=x^ {(k)}-[\dfrac{∂}{∂x^T} F(x^ {(k)})]^{-1} F(x^ {(k)}). \qquad  (4.11)$

Przy naszym określeniu funkcji F, pochodna występująca we wzorze (4.11) to macierz Hessego funkcji f. Wobec tego wzór ten można zapisać następująco

$x^ {(k+1)}=x^ {(k)}-[∇^2 f(x^ {(k)})]^{-1} ∇^T f(x^ {(k)}). \qquad (4.12)$

Mamy więc wzór określający macierz transformacji, nie jest on jednak zależny od „historii” a tylko od macierzy Hessego – „czynnika określającego krzywiznę funkcji celu” – policzonej w bieżącym punkcie.

Stosowanie wzoru (4.12) do znajdowania rozwiązania zadania optymalizacji jest niepraktyczne z dwu powodów.

• Po pierwsze trzeba w nim odwracać macierz, a wiemy że jest to operacja trudna gdy chcemy ją dokładnie wykonać numerycznie.
• Po drugie algorytm Newtona zbiega szybko, bo kwadratowo, do rozwiązania, ale tylko wtedy gdy funkcja f jest taka, że jej macierz Hessego jest w kolejnych punktach odwracalna a algorytm wystartuje w stosownym otoczeniu rozwiązania (zbieżność jest lokalna bo transformacja kierunku wyznaczonego przez gradient jest zależna tyko od informacji bieżącej, a więc lokalnej).

Wobec tego podjęto szereg prób modyfikacji algorytmu Newtona mających na celu zachowanie kwadratowej zbieżności przy wyeliminowaniu konieczności odwracania macierzy i zapewnieniu zbieżności globalnej. 

Przedstawimy teraz podstawowe elementy rozważań, które doprowadziły w drugiej połowie lat sześćdziesiątych XX w. do przedstawienia takich sposobów określania macierzy transformacji, które dały skuteczne algorytmy rozwiązywania zadań optymalizacji.

Rozważania przedstawione w punkcie 3.1.2 pokazały, że dla funkcji klasy $\mathbf{C}^2$ (gładkich) wzór

$x↦\tilde{f} (x;x^ {(k)})=f(x^ {(k)})+∇f(x^ {(k)})(x-x^ {(k)})+\dfrac{1}{2}(x-x^ {(k)} )^T ∇^2 f(x^ {(k)})(x-x^ {(k)})$

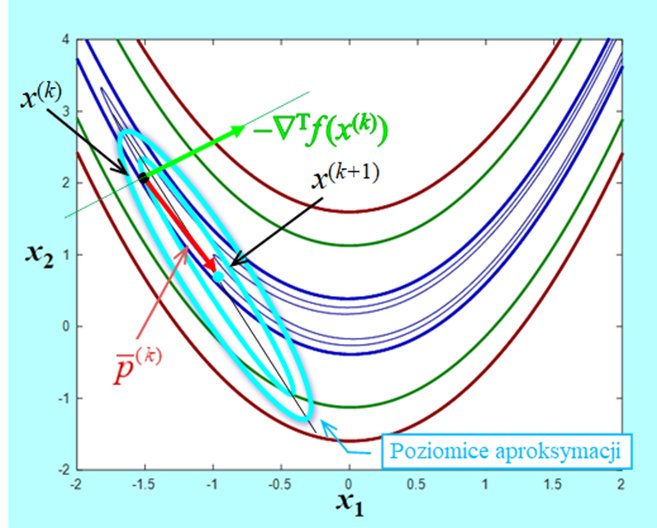
określa aproksymację $\tilde{f}$ funkcji f  w otoczeniu punktu bieżącego $x^{(k)}$. Jeżeli przyjąć za „lokalną” zmienną niezależną przyrost zmiennej po której minimalizujemy w stosunku do punktu bieżącego $p^ {(k)}=x-x^ {(k)},$ to wzór określający zmiany funkcji aproksymującej $\tilde{f}$ w otoczeniu punktu $x^ {(k)}$ w stosunku do jej wartości w tym punkcie $\tilde{f }(x^ {(k)};x^ {(k)})=f(x^ {(k)})$ jest następujący 

Przy naszym podejściu optymisty przyjmujemy, że otoczenie, w którym to przybliżenie daje właściwą informację o zmianach funkcji celu jest duże, co oznacza, że zakładamy, że wektor  $p ̄^ {(k)}$ minimalizujący funkcję (4.13) jest w tym otoczeniu dobrym przybliżeniem kierunku w którym funkcja celu f „najwięcej” zmaleje (pod warunkiem, że macierz Hessego jest dodatnio określona). Funkcja $f_a$ jest dwukrotnie różniczkowalna więc równanie jakie ten wektor musi spełniać jest następujące $∇_{p^ {(k)} } f_a (p ̄^ {(k)};x^ {(k)})=0$ czyli

$∇^2 f(x^ {(k)})p ̄^ {(k)}=-∇^T f(x^ {(k)}).$

Zatem przy założeniu, że $∇^2 f(x^ {(k)})>0$ mamy

$∇f(x^ {(k)})p ̄^ {(k)}=(p ̄^ {(k)} )^T ∇^T f(x^ {(k)})=-(p ̄^ {(k)} )^T ∇^2 f(x^ {(k)})p ̄^ {(k)} < 0, \qquad (4.15)$

co oznacza, że $p ̄^ {(k)}$ jest kierunkiem poprawy i nasze rozumowanie jest poprawne.

Porównując wzory (4.12) i (4.14) łatwo zauważyć, że 

$x^ {(k)}+p ̄^ {(k)}=x^ {(k)}-[∇^2 f(x^ {(k)})]^{-1} ∇^T f(x^ {(k)})=x^ {(k+1)} \qquad(4.16)$

pod warunkiem, że odwrotność macierzy Hessego istnieje, a jak pamiętamy jest tak wtedy gdy np. macierz ta jest dodatnio określona. Oznacza to, że zastosowanie metody stycznych Newtona do rozwiązywania zadania optymalizacji to nic innego jak przyjęcie, że bieżące przybliżenie kwadratowe (4.13) dobrze opisuje zachowanie funkcji minimalizowanej w otoczeniu każdego punktu bieżącego. Zatem z bieżącego punktu należy przejść do punktu w którym funkcja aproksymująca osiąga minimum. W pobliżu lokalnego minimum funkcji celu na pewno takie postępowanie doprowadzi do tego minimum, ale w dużej odległości od niego tak być nie musi, stąd wspomniana wada metody Newtona – gwarantowana zbieżność tylko wtedy gdy algorytm wystartuje w stosownym otoczeniu rozwiązania.

Algorytm Newtona (4.12) jest więc konsekwencją przyjęcia za bieżące przybliżenia funkcji minimalizowanej przybliżenia kwadratowego dla przyrostów $f_a (⋅;x^ {(k)})$ (wzór 4.13) opartego na macierzy drugich pochodnych funkcji celu obliczanej w bieżących punktach, co dało warunek (4.14) jaki musi spełniać wektor $p ̄^ {(k)}$a w konsekwencji pozwoliło wyprowadzić wzór (4.16). 

Szukając sposobów poprawienia algorytmu Newtona twórcy algorytmów optymalizacji w „swoim optymizmie starali się pójść dalej” i zaczęli szukać warunków jakie powinna spełniać funkcja kwadratowa aproksymująca funkcję celu w otoczeniu punktu bieżącego tak aby mogła być podstawą do wyznaczenia lepszego niż newtonowski kierunku poprawy. Po pierwsze, powinna być oparta na dodatnio określonej (a więc odwracalnej) macierzy $D(k)$ zależnej co najmniej od punktu bieżącego $x^ {(k)}.$ Rozważmy taką funkcję, np. o postaci:

$p^ {(k)}↦f_d (p^ {(k)};x^ {(k)})=∇f(x^ {(k)})p^ {(k)}+\dfrac{1}{2}(p^ {(k)} )^T (D^ {(k)} )^{-1} p^ {(k)}, (4.17)$

gdzie, tak jak poprzednio, $p^ {(k)}=x-x^ {(k)}$, jest przyrostem zmiennej po której minimalizujemy w stosunku do punktu bieżącego. Minimum funkcji (4.17) jest dane wektorem spełniającym warunek 

$(D^ {(k)} )^{-1} p ̂^ {(k)}=-∇^T f(x^ {(k)}),$ czyli $p ̂^ {(k)}=-D^ {(k)} ∇^T f(x^ {(k)}). \qquad (4.18)$

Rozumując jak poprzednio, wzór (4.15), można pokazać, że tak wyznaczony kierunek $p ̂^ {(k)}$ jest kierunkiem poprawy dla funkcji f. 

Zauważmy teraz, że dla dowolnych punktów $x^ {(k+1)}$  i  $x^ {(k)}$ mamy następujący wzór na zmianę gradientu funkcji celu f 

Oznacza to, że dla dostatecznie małej różnicy $x^{(k)} – x^{(k+1)}$  dostaniemy

$∇^2 f(x^ {(k+1)})(x^ {(k+1)}-x^ {(k)})≈∇^T f(x^ {(k+1)})-∇^T f(x^ {(k)}).$

Intuicyjnie przyjęto, że macierz $D^{(k)}$ określająca funkcję (4.17) powinna spełniać powyższy warunek dokładnie tzn. (uwzględniając zależność $∇_p^2 f_d (p;x^ {(k+1)})=(D^ {(k+1)} )^{-1})$powinna być spełniona równość

$D^ {(k+1)} (∇^T f(x^ {(k+1)})-∇^T f(x^ {(k)}))=x^ {(k+1)}-x^ {(k)}. \qquad (4.19)$

Wymaganie zapisane równością (4.19) nosi nazwę warunku quasi-newtonowskiego.

Jeżeli teraz przyjmiemy, że wzór określający macierz $D^{(k+1)}$ powinien mieć pamięć długookresową, tzn. być zależny od $D^{(k)}$, to do warunku quasi-newtonowskiego możemy dodać wymaganie

$D^{(k+1)}=D^{(k)}+V^{(k)} \qquad (4.20)$, 

gdzie poprawka $V^{(k)}$zależna co najmniej od punktu bieżącego $x^{(k)}$ powinna dawać dodatnio określoną macierz $D^ {(k+1)}$ gdy macierz $D^ {(k+1)}$ jest też okreslona dodatnio)

Analiza równania (4.19) i wymagania (4.20) pokazała, że poprawka $V^{(k)}$ nie jest określona przez nie jednoznacznie, stąd opracowano wiele wzorów na poprawkę. Z teoretycznego punktu widzenia najciekawsza jest tzw. rodzina poprawek Broydena. Określmy najpierw wektory przyrostów w stosunku do punktu bieżącego:

Dla ustalonej liczby $φ∈[0,1]$ rodzina poprawek Broydena jest określona dla $k = 0,1,2,...$ wzorami

 $V_φ^{(k)}=\dfrac{p^{(k)}(p^{(k)})^T}{(p^{(k)})^T g^{(k)}}-\dfrac{D^{(k)}g^{(k)}(g^{(k)})^T D^((k) )}{(g^{(k)})^T D^{(k)}g^{(k)}}+φτ^{(k)}w^{(k)}(w^{(k)})^T$

$w^ {(k)}=\dfrac{p^ {(k)}}{(p^ {(k)} )^T g^ {(k)} }-\dfrac{D^ {(k)} g^ {(k)}}{τ^ {(k)} },  τ^ {(k)}=(g^ {(k)} )^T D^ {(k)} g^ {(k)}, \qquad (4.21)$,

gdzie $D^{(0)}>0.$

Wzory już od samego patrzenia przyprawiają o gęsią skórkę, ale pomyślcie Państwo o tych co je wyprowadzali. Musieli przecież sprawdzać warunki (4.19) i (4.20)!

Wymagana w warunku (4.20) dodatnia określoność każdej macierzy$D^{(k)}$ gwarantująca, że kierunki $d^ {(k)}=-D^ {(k)} ∇^T f(x^ {(k)})$ będą kierunkami poprawy została „zaszyta” we wzorach (4.21) przy założeniu, że punkt następny $x^ {(k+1)}$, potrzebny do obliczenia przyrostów $p^ {(k)}$ i $g^ {(k)}$, został wyznaczony w wyniku dokładnej minimalizacji w kierunku $d^ {(k)}$, tzn. przy przyjęciu, że ciąg punktów ${x^ {(k)}}$ jest generowany przez algorytm

$\left.\begin{matrix} x^{(0)}\, \mathrm{dane,} \,D^{(0)}>0\, \mathrm{dana}, \, d^{(k)}=-D^{(k)} ∇^T f(x^{(k)} )\\                  α^{(k)}=\mathrm{argmin}_{α ≥0}f (x^{(k)}+αd^{(k)}) \\ x^{(k+1)}=x^{(k)}+α^{(k)}d^{(k)},\\                  D^{(k+1)}=D^{(k)}+V_φ^{(k)}\,\,\,                         k=0,1,2,…\end{matrix}\right\}\qquad (4.22)$

Jeżeli punkt $x^{(k+1)}$ obliczony w oparciu o kierunek $d^ {(k)}=-D^ {(k)} ∇^T f(x^ {(k)})$ zapewnia tylko poprawę funkcji celu w stosunku do wartości w punkcie $x^{(k)}$ (nie stosujemy dokładnej minimalizacji w kierunku), to w praktycznej realizacji algorytmu trzeba zastosować stosowne zabezpieczenie gwarantujące, że kolejny kierunek $d^{(k+1)}$ będzie kierunkiem poprawy. 

Poprawka $V_0^{(k)}$ wyliczona wg wzoru (4.21), w którym położono $φ= 0$ nosi nazwę poprawki Davidona – Fletchera – Powella (poprawki DFP), a poprawka $V_1^{(k)}$wyliczona dla $φ = 1$, to poprawka Broydena – Fletchera – Goldfarba – Shanno (poprawka BFGS), od nazwisk autorów, którzy je wprowadzili – pierwszą na początku lat sześćdziesiątych XX w., a drugą w 1970 roku.

W 1972 r. L.C.W. Dixon pokazał, że z teoretycznego punktu widzenia wszystkie poprawki rodziny Broydena są równoważne – przy dokładnej minimalizacji w kierunku kolejne punkty $x(^{(k)}$ obliczone według wzorów (4.22) są przy użyciu dowolnej z nich takie same. Pokazano także twierdzenie analogiczne do twierdzenia (4.2) o skończonej zbieżność algorytmu kierunków Q-sprzężonych przy stosowaniu do minimalizacji funkcji kwadratowej. ustanawiające skończoną zbieżność algorytmu (4.22) w analogicznym przypadku.

Jak pamiętamy wymaganie jakie musi spełniać macierz transformacji $D^{(n)}$ zapisane równością (4.19) nosi nazwę warunku quasi-newtonowskiego. Stąd wynikła powszechnie używana nazwa algorytmów w których nowy kierunek poprawy $d^{(n)}$ jest określany za pomocą tej macierzy: $d^ {(k)}=-D^ {(k)} ∇^T f(x^ {(k)})$ – są to algorytmy quasi-newtonowskie.  

Twierdzenie 4.2QN wskazuje na związek miedzy algorytmami quasi-newtonowskimi i algorytmami gradientu sprzężonego. Można też wskazać i różnice.

Jeżeli pozbawimy wzór określający macierz transformacji pamięci długookresowej przyjmując w nim $D^{(k-1)}=I$, to wzór określający kolejną macierz transformacji dla poprawki BFGS będzie następujący

$D_I^ {(k)}=I+\dfrac{p^{(k-1)}(p^{(k-1)})^T}{(p^{(k-1)})^T g^{(k-1)}}(1-\dfrac{(g^{(k-1)})^T g^({(k-1)}}{(p^{(k-1)})^T g^{(k-1)}})-\dfrac{g^{(k-1)}(p^{(k-1)})^T+p^{(k-1)}(g^{(k-1)})^T}{(p^{(k-1)})^T g^{(k-1)}}$.

Jeżeli teraz dokonamy dokładnej minimalizacji na kierunku $x^ {(k)}-αD_I^ {(k)} ∇^T f(x^ {(k)})$ otrzymując punkt $x^ {(k+1)},$ to drogą prostych rachunków można pokazać, że

$d^ {(k+1)}=-D_I^ {(k+1)} ∇^T f(x^ {(k+1)})=-∇^T f(x^ {(k+1)})+β^ {(k+1)} d^ {(k)},$

gdzie współczynnik $β^ {(k+1)}$ określony jest wzorem (4.8) lub równoważnym w tym przypadku wzorem (4.9). Oznacza to, że tzw. algorytm BFGS bez pamięci jest równoważny algorytmowi gradientu sprzężonego. Ponieważ pokazaliśmy, że w algorytmie gradientu sprzężonego pamięć długookresowa występuje, to stwierdzenie powyższe można interpretować jako stwierdzenie faktu, że w pełnym algorytmie quasi-newtonowskim poprawny wpływ poprzednich kierunków poprawy na kierunek bieżący jest większy aniżeli w metodzie gradientu sprzężonego, co uzasadnia empirycznie stwierdzoną przewagę (w większości przypadków szybciej zbiegały) tych pierwszych. 

Zebrane w ciągu ponad półwiecza doświadczenia pokazały, że najlepszym algorytmem ogólnego przeznaczenia tj. pierwszym algorytmem jakiego należy użyć gdy zadanie optymalizacji nie ma specjalnych własności (struktury), jest quasi-newtonowski algorytm BFGS. Wypisany wyżej wzór dla algorytmu BFGS bez pamięci jest już wystarczająco skomplikowany, dlatego starano się znaleźć prostszą formułę wzoru pełnego niż zaproponowana oryginalnie. W 1980 roku J. Nocedal podał wzory następujące:

$\begin{matrix} η^ {(k)}=\dfrac{1}{(p^ {(k)} )^T g^ {(k)} },\, W^ {(k)}=I-η^ {(k)} g^ {(k)} (p^ {(k)} )^T\\D^ {(k+1)}=(W^ {(k)} )^T D^ {(k)} W^ {(k)}+η^ {(k)} p^ {(k)} (p^ {(k)} )^T, D^{(0)}>0).\end{matrix} \qquad(4.23)$

Praktyczna realizacja quasi-newtonowskiego algorytmu BFGS może być następująca.

Algorytm quasi-newtonowski  (wersja BFGS z odnową i skalowaniem macierzy początkowej) 

Inicjalizacja

Ustal dokładność algorytmu $\varepsilon > 0.$

Wybierz punkt początkowy $x^{(0)}$, podstaw $x := x^{(0)}.$

Podstaw $k := 0.$

Kroki algorytmu

Omówmy krótko różnice miedzy przedstawionym powyżej algorytmem a jego teoretycznym prototypem danym wzorami (4.22).

• Nie zakładamy dokładnej minimalizacji w kierunku. Musimy zatem liczyć się z tym, że kolejny kierunek $d ^{(k+1)}$ może nie być kierunkiem poprawy. Dlatego wprowadzono krok szósty wywołujący odnowę gdy trzeba „sprowadzić algorytm ze złej drogi”. Ponadto, podobnie jak dla algorytmu gradientu sprzężonego, wprowadzono odnowę, tym razem co $2n + 1$ kroków. Liczba ta wzięła się z wieloletnich doświadczeń i uwzględnia fakt, że algorytm BFGS stosuje się często do znajdowania rozwiązania zadań o niewielkiej wymiarowości.

• Wzór (4.21), a za nim zastosowany w algorytmie wzór (4.23), nie określa jak wybierać macierz początkową $D^{(0)}$. Jedyne wymaganie to jej dodatnia określoność. Najprostszy pomysł to wybranie jako początkowej – macierzy jednostkowej. Praktyka jednak pokazała, że istotne przyspieszenie zbieżności początkowych iteracji można uzyskać skalując w sposób dobrany do własności zadania tę macierz. Przedstawiono stosowne nieco skomplikowane rozważania pozwalające określić dla pewnych klas zadań wzory ustalające wartość współczynnika skalującego. Z drugiej strony swój korzystny wpływ na szybkość zbieżności algorytmu dla wielu różnych zadań, tzn. swoją uniwersalność, potwierdził współczynnik określony prostym wzorem

$γ=\dfrac{(x^{(1)}-x^{(0)})^T (∇^T f(x^{(1)})-∇^T f(x^{(0)}))}{(∇f(x^{(1)})-∇f(x^{(0)}))(∇^T f(x^{(1)})-∇^T f(x^{(0)}))}$.

• Algorytm BFGS, jak wszystkie algorytmy quasi-newtonowskie, jest algorytmem, który opiera się na założeniu, że funkcja kwadratowa dobrze aproksymuje zachowanie funkcji minimalizowanej w dostatecznie dużym otoczeniu punktu bieżącego. Badania teoretyczne pokazały, że do udowodnienia zbieżności np. sama wypukłość funkcji celu nie wystarczy. Ponieważ, po pierwsze – nikomu nie chce się sprawdzać tych warunków (najczęściej jest to co najmniej trudne) i po drugie – praktyka pokazała, że algorytmy quasi-newtonowskie potrafią znaleźć rozwiązanie i dla zadań nie spełniających tych założeń, pod warunkiem, że wystartują z dobrego punktu początkowego, to w praktycznych wariantach tych algorytmów stosuje się co z góry ustaloną liczbę (w naszym przypadku $2n + 1)$ kroków odnowę. Jak pamiętamy gwarantuje to przy słabych założeniach: różniczkowalności funkcji celu i lipschitzowości jej gradientu, że dolna granica ciągu, którego elementami są normy gradientu liczone w kolejnych punktach wyliczanych przez algorytm, jest równa zeru, nawet bez konieczności dokonywania dokładnej minimalizacji w kierunku. Podobnie jak dla algorytmów gradientu sprzężonego przy mocniejszych założeniach pokazano, że algorytmy quasi-newtonowskie zbiegają superliniowo do punktu minimalizującego.

Przedstawimy teraz krótkie porównanie zachowania quasi-newtonowskiego algorytmu BFGS bez odnowy z algorytmem gradientu sprzężonego w wersji PPR minimalizujących bananową funkcję Rosenbrocka. W obu algorytmach minimalizacja w kierunku wykorzystywała wielomian interpolacyjny.

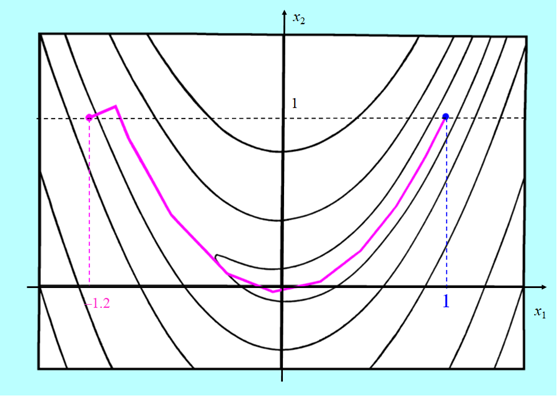
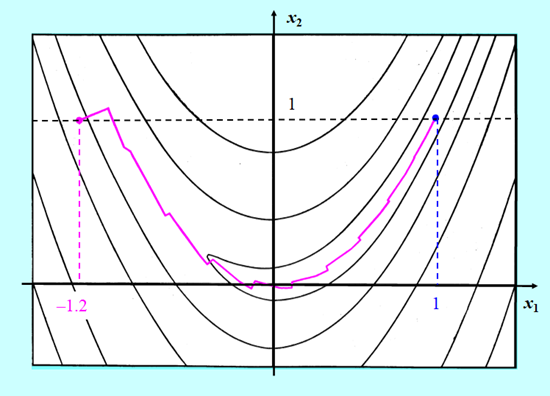
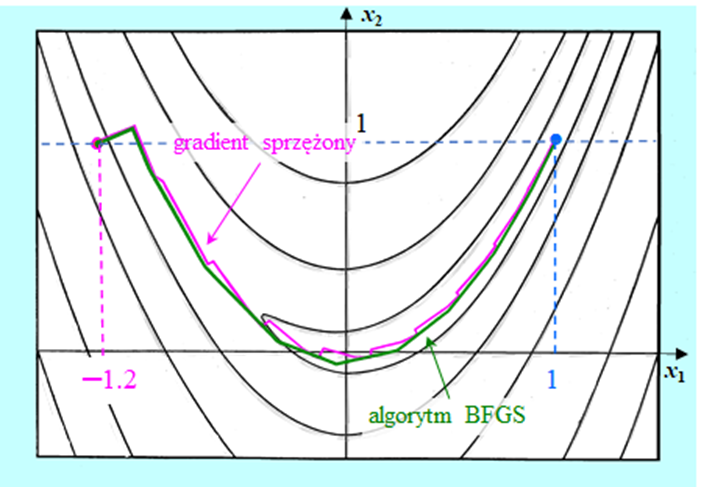
Algorytm gradientu sprzężonego zużył 24 iteracje na dotarcie do rozwiązania, a quasi-newtonowskiemu algorytmowi BFGS wystarczyło tylko 11 iteracji.

Przedstawione rysunki pokazują wyższość algorytmu BFGS. Nie jest to przypadek. Szerokie badania porównawcze prowadzone od początku lat osiemdziesiątych XX w. wykazały, że algorytm ten, jak już wspomniano, jest pierwszym algorytmem jakim należy się posłużyć gdy zadanie optymalizacji nie ma specjalnych własności (struktury) – jest najefektywniejszym algorytmem ogólnego przeznaczenia dla zadań o niezbyt dużej wymiarowości.