Podręcznik

1. Wprowadzenie do grafów

Graf to jedna z podstawowych i najbardziej uniwersalnych struktur danych w informatyce i matematyce dyskretnej. Jest to zbiór wierzchołków (nazywanych również punktami lub nodami), pomiędzy którymi istnieją połączenia – zwane krawędziami. Grafy służą do modelowania relacji między obiektami, co sprawia, że mają szerokie zastosowanie w wielu dziedzinach, takich jak informatyka, logistyka, sieci komputerowe, biologia, ekonomia czy teoria baz danych.

Zazwyczaj graf przedstawia się za pomocą symboli G = (V, E), gdzie V jest to zbiór wierzchołków grafu, zwanych również węzłami (ang. vertex), natomiast E to zbiór krawędzi grafu (ang. edge).

Grafy dzielimy zasadniczo na dwa rodzaje – grafy skierowane oraz nieskierowane.

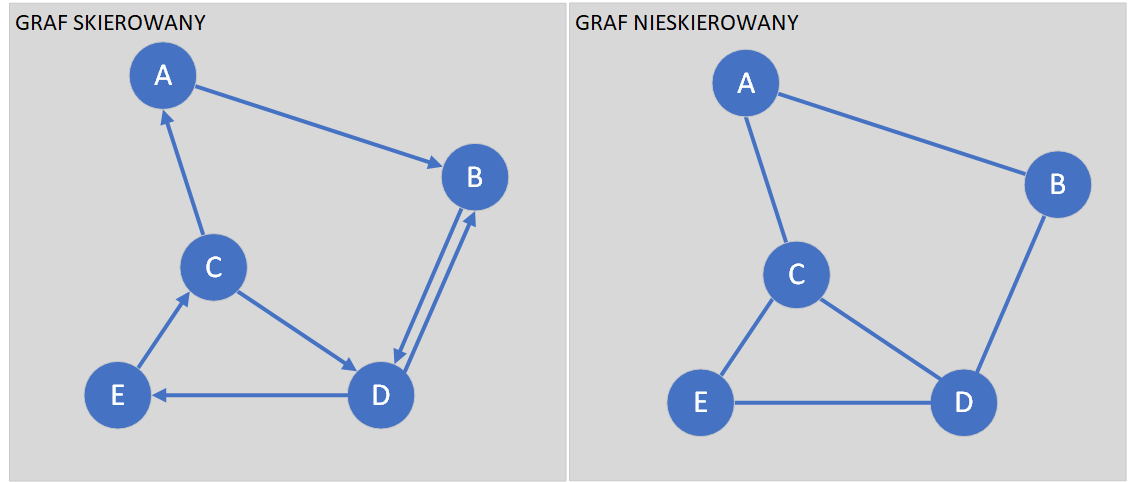
Najczęściej w pamięci grafy przechowywane są za pomocą:

list sąsiedztwa,
macierzy sąsiedztwa.

Lista sąsiedztwa są strukturą danych, w której dla każdego wierzchołka przechowywana jest lista wierzchołków, z którymi ma on bezpośrednie połączenia (czyli sąsiadów). Reprezentacja ta stanowi bardzo efektywna pamięciowo w przypadku grafów rzadkich, czyli takich, gdzie liczba krawędzi jest znacznie mniejsza niż maksymalna możliwa liczba połączeń. Dla każdego wierzchołka tworzy się osobną listę (lub tablicę dynamiczną), w której umieszczane są wszystkie sąsiednie wierzchołki. Ta reprezentacja pozwala na szybki dostęp do listy sąsiadów danego węzła, a dodawanie krawędzi odbywa się w czasie stałym. Możliwe są dwie wersje list sąsiedztwa: lista węzłów, do których prowadzą krawędzie wychodzące z danego wierzchołka oraz lista węzłów, z których prowadzą krawędzie przychodzące do danego wierzchołka.

Dla grafu nieskierowanego przedstawionego na rysunku powyżej lista sąsiedztwa będzie wyglądała następująco:

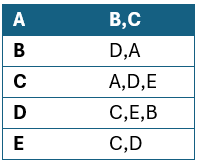
W przypadku grafu skierowanego istotne jest czy w zapisie uwzględniamy węzły skierowane od danego wierzchołka, czy odwrotnie. W przypadku grafu skierowanego nie ma to znaczenia.

Macierz sąsiedztwa natomiast to kwadratowa tablica dwuwymiarowa o rozmiarze

$nxn$ , gdzie 𝑛 to liczba wierzchołków w grafie. Wartość na pozycji ( 𝑖 , 𝑗 ) w tej tablicy wskazuje, czy istnieje krawędź pomiędzy wierzchołkiem 𝑖 a 𝑗 . W grafach ważonych ta wartość może odpowiadać wagom krawędzi. Macierz sąsiedztwa umożliwia bardzo szybkie sprawdzenie istnienia połączenia między dowolnymi dwoma wierzchołkami wystarczy jedno odwołanie do elementu tablicy. Jednak jej główną wadą jest duże zużycie pamięci, zwłaszcza w przypadku grafów rzadkich, ponieważ wymaga przechowywania

$n^2$ wartości, niezależnie od rzeczywistej liczby krawędzi.

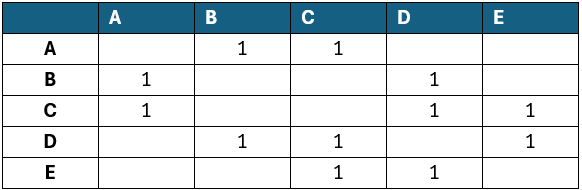
Podsumowując, reprezentacja grafu jako lista sąsiedztwa jest bardziej oszczędna pamięciowo i lepiej sprawdza się w grafach rzadkich, natomiast macierz sąsiedztwa oferuje szybszy dostęp do informacji o krawędziach, co może być korzystne w gęstych grafach lub w algorytmach często sprawdzających istnienie połączeń między wierzchołkami. Wybór reprezentacji powinien więc zależeć od charakterystyki konkretnego problemu i rodzaju wykonywanych operacji.

Przeszukiwanie grafów w głąb

Przeszukiwanie w głąb (ang. Depth-First SearchDFS) polega na eksploracji grafu „najdalej jak się da” tzn. zanim wróci się i zacznie badać inne możliwe ścieżki. Zazwyczaj jest realizowane rekurencyjnie lub przy użyciu stosu. Algorytm DFS odwiedza sąsiadów wierzchołka, następnie sąsiadów tych sąsiadów, i tak dalej, aż dotrze do punktu, w którym nie można już pójść głębiej – wtedy algorytm się cofa i kontynuuje badanie pozostałych gałęzi. Przeszukiwanie w głąb doskonale sprawdza się w przypadkach, gdy zależy nam na pełnym zbadaniu struktur rozgałęzionych, takich jak drzewa, i jest fundamentem np. algorytmu Tarjana do znajdowania punktów artykulacji czy mostów w grafie.

lgorytm przeszukiwania w głąb może być stosowany zarówno dla grafów nieskierowanych, jak i dla grafów skierowanych. Działa również poprawnie dla obu rodzajów grafów w przypadku innego podziału – dla grafów spójnych i niespójnych. Teraz jest więc już najwyższy czas na wprowadzenie ich definicji.

Graf nazywamy spójnym, gdy między dwoma jego dowolnymi wierzchołkami istnieje łącząca je ścieżka (czyli z dowolnego miejsca w grafie można dotrzeć do każdego innego). Jeśli graf nie posiada takiej cechy, to jest on grafem niespójnym.

W przypadku grafu spójnego procedura odwiedzDFS będzie wywołana tylko jeden raz wewnątrz procedury DFS (gdyż „za jednym zamachem” zostaną odwiedzone wszystkie wierzchołki grafu – z definicji są one osiągalne z węzła początkowego). Natomiast dla grafu niespójnego procedura ta będzie uruchamiana kilkakrotnie. W przypadku grafów skierowanych spójność grafów można podzielić na dwie grupy: słabą spójność oraz silną spójność.

Graf skierowany jest słabo spójny, jeśli odpowiadający mu graf nieskierowany (czyli po odrzuceniu kierunków krawędzi) jest spójny. Natomiast graf jest silnie spójny, gdy dla dowolnej pary węzłów u i v można znaleźć ścieżkę prowadząca zarówno z u do v, jak i z v do u.

Przeszukiwanie grafów wszerz

Przeszukiwanie grafu wszerz (ang. Breadth-First Search - BFS) – to druga podstawowa technika odwiedzania wierzchołków grafu. W przeciwieństwie do DFS, która „schodzi” najgłębiej jak się da w grafie, zanim się cofnie, BFS przeszukuje graf „poziomami”, czyli najpierw odwiedza wszystkich sąsiadów danego wierzchołka, a dopiero potem przechodzi do ich sąsiadów. Do realizacji algorytmu BFS potrzebna jest reprezentacja grafu (najczęściej lista sąsiedztwa) oraz struktura kolejki, w której przechowywane są wierzchołki oczekujące na odwiedzenie. Wierzchołki odwiedzone są zaznaczane w pomocniczej tablicy odwiedzony, dzięki czemu nie trafiają ponownie do kolejki. Algorytm rozpoczyna się od zainicjowania stanu wszystkich wierzchołków jako nieodwiedzonych. Następnie do kolejki wrzucany jest wierzchołek startowy, oznaczany jako odwiedzony. Algorytm w pętli wyciąga kolejne wierzchołki z kolejki, przetwarza je (np. wypisuje), a wszystkich ich nieodwiedzonych sąsiadów dodaje na koniec kolejki i oznacza jako odwiedzonych. Proces trwa do momentu, aż kolejka stanie się pusta, co oznacza, że odwiedzono wszystkie wierzchołki dostępne z punktu startowego. BFS pozwala bardzo efektywnie wyznaczać najkrótszą ścieżkę w grafach nieskierowanych i nieskrajnie ważonych (tzn. gdy wagi wszystkich krawędzi są równe). Ponadto jest używany w wielu klasycznych algorytmach grafowych, m.in. w rozpoznawaniu składowych spójnych, wykrywaniu cykli czy znajdowaniu minimalnych ścieżek.

BFS jest zwykle implementowany iteracyjnie i ma złożoność czasową O(V + E), gdzie V to liczba wierzchołków, a E – liczba krawędzi. To czyni go bardzo wydajnym narzędziem w analizie struktur grafowych, szczególnie wtedy, gdy zależy nam na eksploracji szerokości drzewa odwiedzin.