Podręcznik
1. Optymalizacja
Po co nam optymalizacja?
Wyobraźmy sobie codzienne sytuacje: chcemy dojechać do pracy jak najszybciej, wybrać najtańszy lot na wakacje czy zaprojektować konstrukcję mostu, który wytrzyma największe obciążenia przy jak najniższym koszcie. We wszystkich tych przypadkach chodzi o to samo: znaleźć najlepsze możliwe rozwiązanie, zgodne z przyjętym kryterium.
Tym właśnie zajmuje się optymalizacja. Matematycznie rzecz ujmując, optymalizacja to poszukiwanie minimum lub maksimum funkcji celu przy zadanych ograniczeniach. Funkcja celu to matematyczny opis tego, co chcemy zmaksymalizować (np. zysk) lub zminimalizować (np. koszt). Zmiennymi decyzyjnymi są parametry, które możemy kontrolować, a ograniczenia to zbiór warunków, które rozwiązanie musi spełniać, by było dopuszczalne.
Optymalizacja pojawia się wszędzie tam, gdzie trzeba podejmować decyzje. Trzeba jednak pamiętać, że nie każda decyzja intuicyjnie najlepsza jest naprawdę optymalna w sensie matematycznym — różnica ta staje się istotna w zastosowaniach inżynierskich czy ekonomicznych, gdzie nieoptymalny wybór może skutkować realnymi stratami.
Trudności w optymalizacji
Pierwszą trudnością w wielu problemach optymalizacyjnych jest rozmiar przestrzeni poszukiwań. Gdy liczba zmiennych jest duża, liczba możliwych rozwiązań rośnie wykładniczo, a pełne przeszukiwanie staje się praktycznie niemożliwe. Przykładowo, przy 100 zmiennych binarnych mamy do rozważenia wariantów. Nawet najpotężniejsze komputery nie są w stanie przetworzyć takiej ilości danych w sensownym czasie.
Drugi problem to natura samej funkcji celu. W praktyce funkcje te są często nieliniowe, nieciągłe, a czasem nawet stochastyczne. Może się okazać, że drobna zmiana parametrów powoduje duży i nieprzewidywalny skok wartości funkcji celu. Taka „dzika” topologia przestrzeni rozwiązań utrudnia klasyczne metody optymalizacji bazujące na pochodnych i gradientach.
Trzecią barierą są ograniczenia — formalne lub ukryte. Wiele rzeczywistych problemów zawiera trudne do opisania warunki dopuszczalności: fizyczne, techniczne, prawne, czy związane z bezpieczeństwem. Dodanie ich do modelu optymalizacyjnego komplikuje analizę i znacząco zmniejsza liczbę dopuszczalnych rozwiązań, często do bardzo nieregularnych obszarów.
Ostatni, ale nie mniej ważny problem to lokalne ekstrema. W przypadku funkcji nieliniowych algorytmy mogą „utknąć” w minimum lokalnym — rozwiązaniu, które wygląda na dobre, ale nie jest najlepsze globalnie. Problem ten jest szczególnie dotkliwy w optymalizacji dyskretnej i złożonych problemach inżynierskich, gdzie nie widać łatwej drogi ucieczki z takiego minimum bez globalnej wiedzy o przestrzeni rozwiązań
Przykłady zastosowania optymalizacji
Poniżej przedstawiamy kilka klasycznych przykładów pokazanych na slajdach prezentacji AE1 2020.
Optymalizacja konstrukcji
Transport 1000 m³ chemikaliów ma się odbywać w szczelnych, prostopadłościennych pojemnikach. Każdy pojemnik ma ściany boczne nazywane odpowiednio A i B, oraz dno i górę. Każdy pojemnik można zbudować przy zachowaniu konkretnych warunków:
- materiał na górę kosztuje 65 PLN za metr kwadratowy
- materiał na boki A kosztuje 35 PLN za metr kwadratowy
- materiał na boki B oraz dno jest dostępny za darmo (pochodzi z odpadów), natomiast jest ograniczenie w jego ilości - możemy wykorzystać nie więcej niż 10 metrów kwadratowych na pojemnik
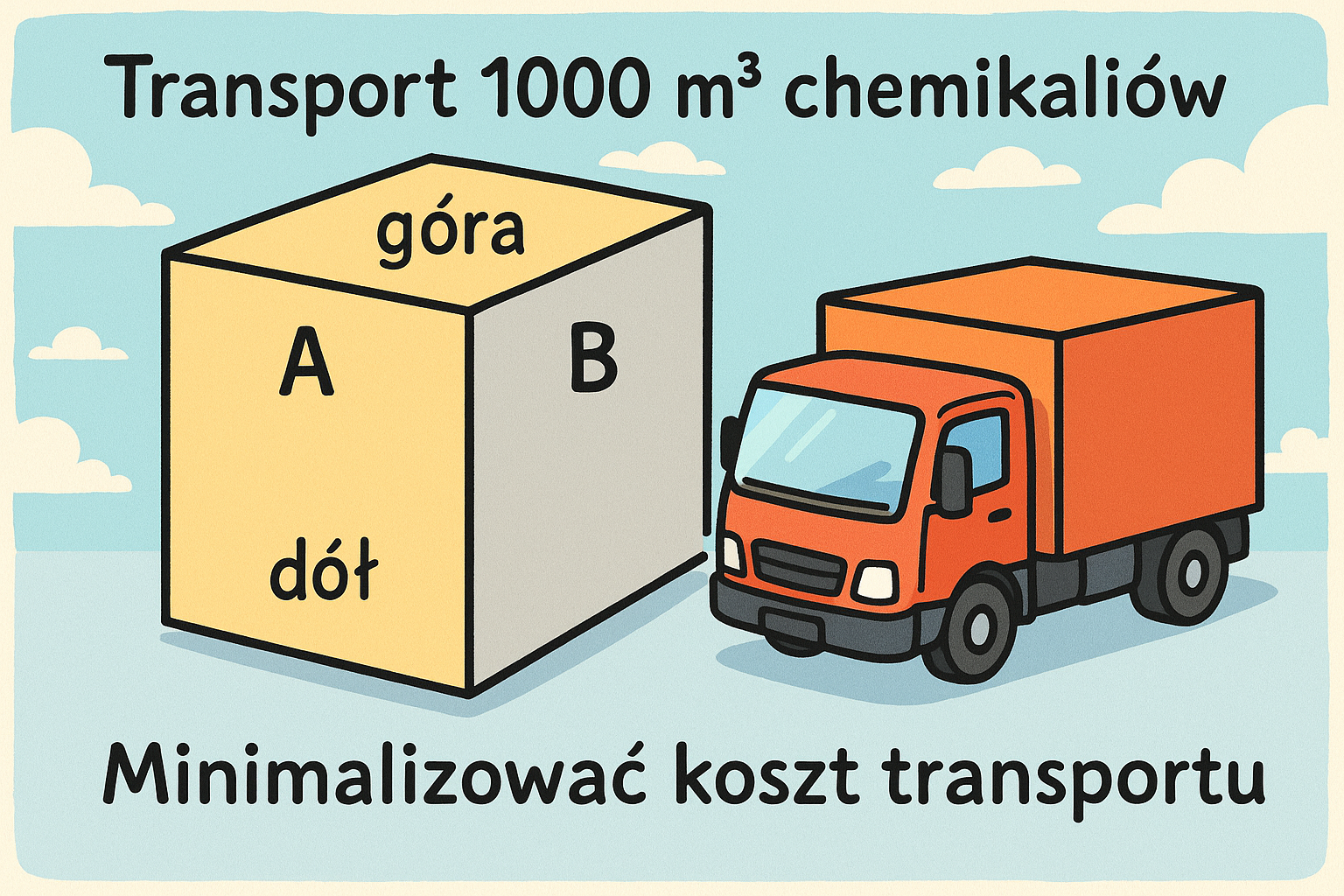
Transport pojemnika kosztuje 4 PLN, niezależnie od jego wielkości. Celem jest minimalizacja kosztu transportu. To klasyczny przykład zadania liniowego z ograniczeniami — zmienne decyzyjne to wymiary pojemników, a funkcja celu może zależeć np. od kosztów materiałów i liczby pojemników.
\(
k_j(x_1, x_2, x_3) = km_A \cdot 2(x_2 \cdot x_3) + km_{góra} \cdot (x_1 \cdot x_2) + k_{transport} \)
gdzie:
\(\begin{align*}
x_3 &\text{ — wysokość pojemnika,} \\
x_1 &\text{ — szerokość pojemnika,} \\
x_2 &\text{ — głębokość pojemnika,} \\
k_{transport}&\text{ — koszt transportu pojedynczego pojemnika}
\end{align*}\)
Znając wymiary pojemnika możemy też obliczyć ile ich potrzebujemy:
\( z= \frac{V_{całkowita}}{x_1*x_2*x_3} \)
No i finalnie dochodzimy do wzoru na koszt całkowity
\( f(x_1,x_2,x_3)=z*k_j = \frac{V_{całkowita}}{x_1*x_2*x_3} * (km_A \cdot 2(x_2 \cdot x_3) + km_{góra} \cdot (x_1 \cdot x_2) + k_{transport} ) \)
Optymalizacja portfela inwestycyjnego
Optymalizacja portfela inwestycyjnego to jeden z klasycznych przykładów zastosowania metod optymalizacyjnych w finansach. Wyobraźmy sobie inwestora, który dysponuje pewnym kapitałem i chce go ulokować w różnych aktywach: np. akcjach dużych stabilnych spółek (tzw. blue chips), sektorze paliwowym, nieruchomościach oraz obligacjach. Każde z tych aktywów cechuje się określoną historyczną stopą zwrotu oraz zmiennością (czyli ryzykiem). Celem inwestora jest znalezienie takiego podziału środków, który zapewni możliwie wysoki zysk przy jednocześnie możliwie niskim ryzyku.
Zmiennymi decyzyjnymi w tym przypadku są procentowe udziały kapitału przeznaczone na każdą z czterech kategorii inwestycji, oznaczmy je odpowiednio jako x₁, x₂, x₃, x₄. Suma tych udziałów musi być równa 1 (czyli 100%), co stanowi podstawowe ograniczenie zadania. Dodatkowo mogą występować ograniczenia dolne i górne, np. minimalny udział w obligacjach albo maksymalny udział w akcjach wysokiego ryzyka.
| Typ inwestycji | Roczna stopa zwrotu | ||||||
|---|---|---|---|---|---|---|---|
| Rok | 1 | 2 | 3 | 4 | 5 | 6 | średnia |
| Blue Chip | 18,24 | 12,12 | 15,23 | 5,26 | 2,62 | 10,42 | 10,65 |
| Paliwa | 12,24 | 19,16 | 35,07 | 23,46 | -10,62 | -7,43 | 11,98 |
| Nieruchomości | 8,23 | 8,96 | 8,35 | 9,16 | 8,05 | 7,29 | 8,34 |
| Obligacje | 8,12 | 8,95 | 8,26 | 8,34 | 9,01 | 9,12 | 8,63 |
Funkcja celu w tym problemie ma charakter dwuwymiarowy. Z jednej strony chcemy zmaksymalizować średnią wartość zysku (czyli kombinację średnich stóp zwrotu poszczególnych aktywów ważonych przez x₁ do x₄), a z drugiej strony zminimalizować ryzyko, które najczęściej mierzy się poprzez wariancję lub odchylenie standardowe wartości portfela.
\( V_{j j}=\frac{1}{n} \sum_{k=1}^n\left(r_{j k}-\mu_j\right)^2 \)
Wariancja całego portfela nie zależy tylko od wariancji poszczególnych aktywów, ale również od ich kowariancji — czyli tego, jak bardzo dane aktywa „poruszają się razem”. Dlatego do zadania wprowadza się macierz kowariancji pomiędzy wszystkimi parami inwestycji. Każda komórka tej macierzy pokazuje wariancję wzajemną:
\( V_{i j}=\frac{1}{n} \sum_{k=1}^n\left(r_{i k}-\mu_i\right)\left(r_{j k}-\mu_j\right) \)
Teraz możemy już zapisać ryzyko:
\(
\text{Ryzyko} = \mathbf{x}^T \mathbf{V} \mathbf{x}
\)
Potem powinniśmy jeszcze uwzględnić ograniczenia (zmienne decyzyjne muszą sumować się do jedynki - musimy podzielić całe środki, i jednocześnie nie przekroczyć budżetu). Drugim ograniczeniem będzie zysk - chcemy mieć średni zysk co najmniej 10%:
\( 10.65*x_1+11.98*x_2+8,34*x_3+8,64*x_4 \geq10 \)
Ostatecznie zadaniem można zapisać jako
\( min {x^TVx} \)
Z ograniczeniami podanymi wyżej, przy dodatkowym założeniu, że żadna ze zmiennych decyzyjnych nie może być mniejsza od zera.
Formalnie zapisane, zadanie optymalizacji portfela przyjmuje postać problemu kwadratowego z ograniczeniami. Funkcja celu jest funkcją kwadratową (ze względu na macierz kowariancji), a ograniczenia mają postać równań liniowych (suma udziałów równa 1) oraz ewentualnie nierówności (udziały nieujemne, minimalne progi). Dodatkowy warunek na minimalny oczekiwany zysk — np. inwestor deklaruje, że chce mieć co najmniej 10% średniego zwrotu - też jest ograniczeniem liniowym.
Tego rodzaju problemy są idealnym kandydatem dla zastosowania algorytmów ewolucyjnych, zwłaszcza gdy w grę wchodzą nieliniowe zależności, dyskretne zmienne (np. minimalny próg inwestycyjny), nietypowe ograniczenia lub wiele konkurencyjnych celów naraz (np. zysk, ryzyko, płynność). Algorytmy genetyczne pozwalają łatwo modelować takie złożone sytuacje i znaleźć zbiór kompromisowych rozwiązań — tzw. front Pareto — dający inwestorowi wachlarz dobrze zbilansowanych opcji inwestycyjnych.
Alokacja zasobów (środek owadobójczy)
Wyobraźmy sobie plantację w kształcie kwadratu, na której zlokalizowano 12 aktywnych gniazd os. Każde z nich stanowi zagrożenie dla ludzi i upraw, dlatego konieczne jest ich unieszkodliwienie. Do dyspozycji mamy trzy pojemniki ze środkiem owadobójczym, które należy rozmieszczać na tej przestrzeni w taki sposób, by skutecznie zneutralizować jak największą liczbę gniazd.
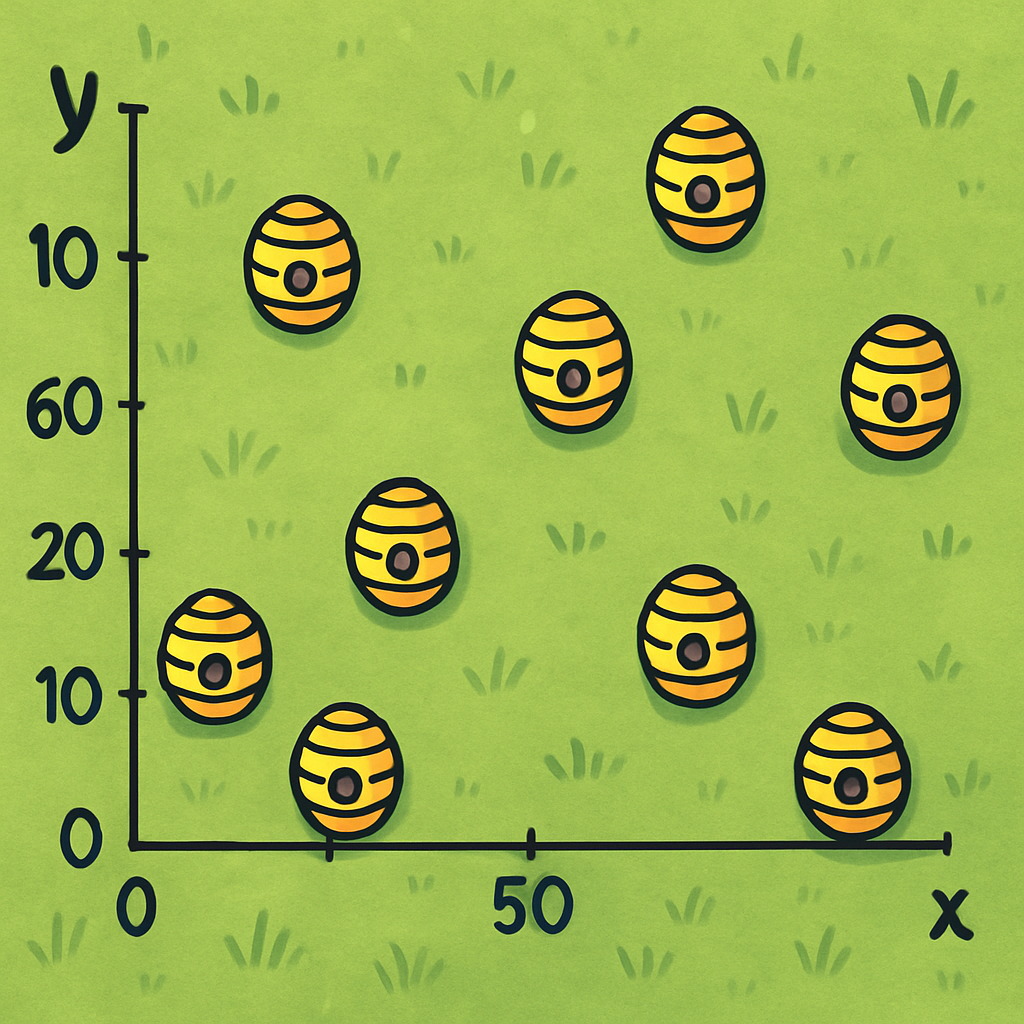
Zmiennymi decyzyjnymi w tym problemie są współrzędne położenia każdego z trzech pojemników, co oznacza, że mamy do czynienia z problemem optymalizacji w przestrzeni sześciowymiarowej: (x₁, y₁, x₂, y₂, x₃, y₃). Każdy punkt w tej przestrzeni określa możliwe ustawienie pojemników na polu. Ograniczenia wynikają z fizycznych granic plantacji (np. wszystkie współrzędne muszą mieścić się w zakresie od 0 do 100 metrów, jeśli pole ma 100 m długości) oraz z odległości minimalnych między pojemnikami (np. ze względów bezpieczeństwa nie mogą znajdować się zbyt blisko siebie).
Funkcja celu opisuje skuteczność działania rozmieszczenia. Załóżmy, że każdy pojemnik działa w sposób radialny — jego skuteczność maleje z odległością od centrum działania. Możemy przyjąć model, w którym środek owadobójczy działa z pełną skutecznością w promieniu np. 10 m, a dalej jego efektywność spada np. wykładniczo. Dla każdego gniazda obliczamy wtedy skumulowany wpływ wszystkich pojemników i określamy, czy dawka przekracza próg skuteczności. Jeśli tak — gniazdo uznaje się za unieszkodliwione.
W ten sposób funkcja celu przyjmuje postać nieliniową i niegładką: jest to liczba gniazd os, które udało się zneutralizować przy danym ustawieniu pojemników. Funkcja ta może mieć wiele lokalnych maksimów (np. ustawienia pojemników skupiające się na części pola) i dlatego stanowi poważne wyzwanie dla klasycznych metod optymalizacji bazujących na pochodnych.
Dodatkową trudnością jest to, że zmienne są ciągłe, a przestrzeń rozwiązań nie jest prostą siatką — ma nieregularny kształt. Oznacza to, że metody optymalizacji wymagają inteligentnych strategii przeszukiwania, które potrafią unikać minimum lokalnych i są odporne na brak ciągłości lub nieregularność funkcji celu. Algorytmy genetyczne doskonale się w tym sprawdzają — operując populacją rozwiązań i stosując operatory krzyżowania i mutacji, mogą eksplorować różnorodne konfiguracje rozmieszczenia pojemników i z czasem wyłaniać te najbardziej skuteczne.
To przykład zadania nieliniowego z ograniczeniami, gdzie przestrzeń poszukiwań jest ciągła, ale funkcja celu — nieliniowa i trudna do zapisania analitycznie.
Optymalizacja produkcji
Przykład optymalizacji produkcji dotyczy zakładu przemysłowego, który wytwarza dwa rodzaje produktów przy użyciu dwóch różnych procesów technologicznych i dwóch rodzajów surowców: A i B. Zakład musi zaspokoić określone zapotrzebowanie rynkowe (np. 30 jednostek produktu X i 20 jednostek produktu Y), a jednocześnie działa w warunkach ograniczeń zasobów (np. dostępność 60 jednostek surowca A i 90 jednostek surowca B).
Zmiennymi decyzyjnymi są liczby cykli produkcyjnych w procesach I i II, oznaczane jako x₁ i x₂. Każdy cykl zużywa określoną ilość surowców A i B oraz dostarcza określoną liczbę produktów X i Y. Znając macierz współczynników technologicznych (ile surowca zużywa dany proces, ile produktu wytwarza), można sformułować model matematyczny całego systemu produkcyjnego.
Celem jest maksymalizacja zysku — różnicy między przychodem ze sprzedaży produktów a kosztem zużycia surowców. Zakłada się, że produkty X i Y mają znane ceny jednostkowe, a surowce A i B — znane koszty jednostkowe. Funkcja celu to więc wyrażenie liniowe zależne od zmiennych x₁ i x₂. Ograniczenia obejmują:
-
dostępność surowców: łączne zużycie A i B w obu procesach nie może przekroczyć ich dostępnych zasobów,
-
minimalne zamówienia: produkcja X i Y musi pokrywać popyt,
-
nieujemność zmiennych: liczba cykli produkcyjnych nie może być ujemna.
Formalnie jest to typowe zadanie programowania liniowego z ograniczeniami liniowymi. Rozwiązanie można znaleźć metodami klasycznymi (np. Simplex), ale w sytuacjach bardziej złożonych — np. gdy:
-
liczba produktów lub procesów wzrasta,
-
pojawiają się nieliniowe koszty (np. rabaty przy dużych zamówieniach),
-
występują zależności logiczne lub dyskretne zmienne (np. ograniczona liczba maszyn, minimalna seria produkcyjna), warto sięgnąć po algorytmy metaheurystyczne.
Algorytmy genetyczne dobrze radzą sobie w takich warunkach. Dzięki pracy na populacji rozwiązań i mechanizmowi selekcji, krzyżowania oraz mutacji są w stanie znajdować rozwiązania nie tylko poprawne, ale często zaskakująco dobre — zwłaszcza w przestrzeniach rozwiązań, w których metody klasyczne zawodzą lub wymagają znacznego uproszczenia modelu.
Celem jest maksymalizacja zysku. Zmiennymi są liczby cykli produkcyjnych dla obu typów procesów. Ograniczenia obejmują zużycie surowców i wymagania produkcyjne. To typowe zadanie liniowe z ograniczeniami.
Sterowanie napędem prądu stałego (DC)
Sterowanie napędem prądu stałego to klasyczny problem z zakresu automatyki, w którym celem jest tak dobrać parametry regulatora, aby układ reagował szybko, bez przeregulowań i z jak najmniejszym błędem ustalonym. Tu rozpatrujemy przypadek optymalizacji odpowiedzi skokowej układu napędowego z regulatorem typu PID (proporcjonalno-całkująco-różniczkującego).
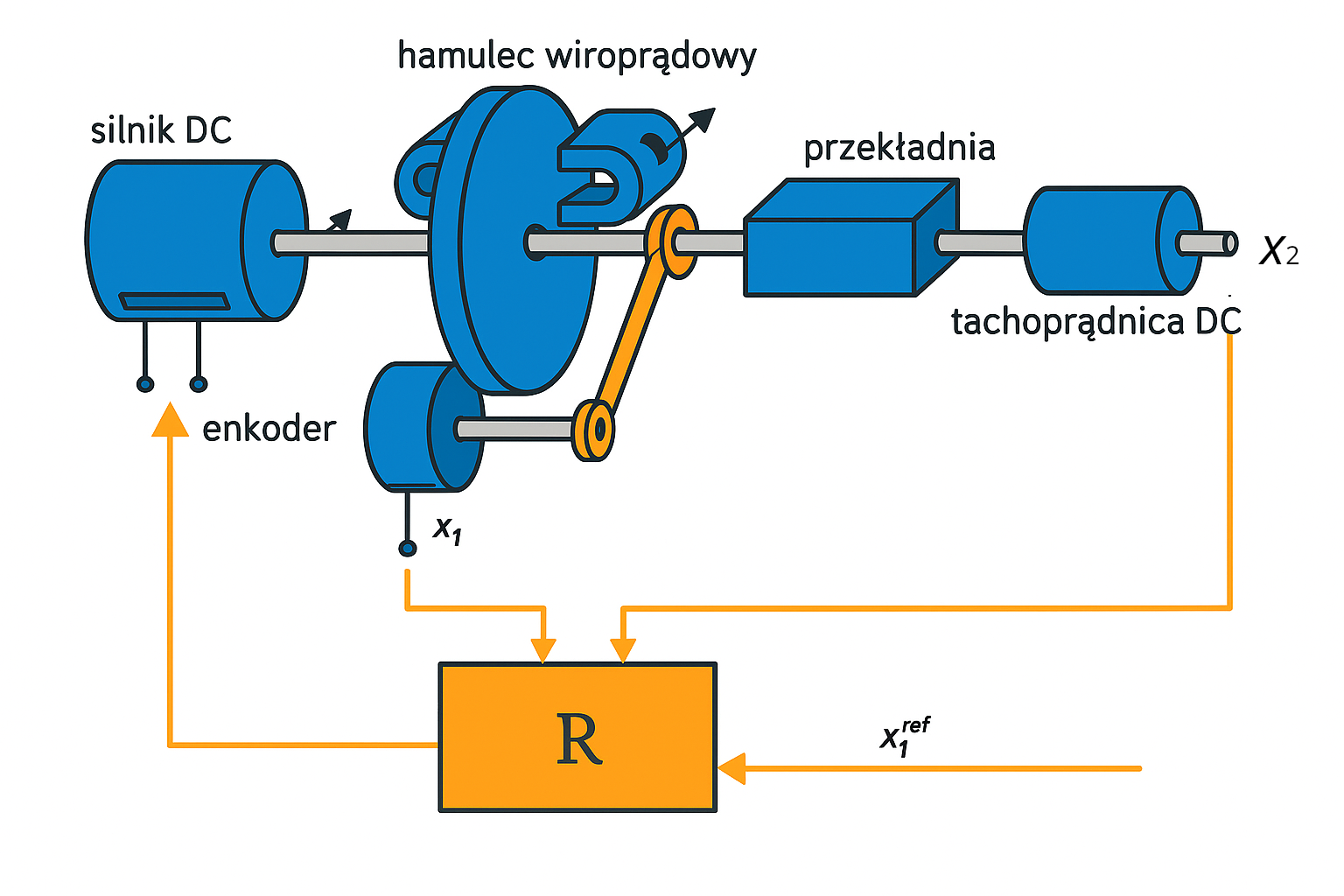
Zmiennymi decyzyjnymi w tym zadaniu są trzy współczynniki regulatora PID: Kₚ (wzmocnienie proporcjonalne), Tᵢ (czas całkowania) i Td (czas różniczkowania). To właśnie od ich wartości zależy jakość odpowiedzi układu: czas osiągania wartości zadanej, poziom przeregulowania oraz tłumienie oscylacji.
Aby ocenić jakość działania danego zestawu parametrów, definiujemy funkcję celu, która wyraża kompromis między różnymi wskaźnikami jakości regulacji. Najczęściej stosuje się kombinację:
- całkowego wskaźnika błędu (IAE, ISE lub ITAE),
- czasu regulacji (czas potrzebny do osiągnięcia zadanego poziomu z tolerancją),
- oraz maksymalnego przeregulowania.
W zależności od wag przypisanych poszczególnym składnikom funkcji celu, możemy preferować szybsze dojście do zadanej wartości kosztem większego przeregulowania, lub odwrotnie — stabilność kosztem szybkości.
Symulacja odpowiedzi skokowej dla każdego zestawu parametrów odbywa się numerycznie, najczęściej z użyciem pakietów typu MATLAB/Simulink lub podobnych narzędzi. Funkcja celu ma charakter nieliniowy i czarno-skrzynkowy, co oznacza, że nie jest znana w postaci analitycznej, a jej wartość można jedynie wyznaczyć przez symulację.
To czyni zadanie trudnym dla klasycznych metod optymalizacji gradientowej, ale bardzo dobrze przystosowanym do podejść ewolucyjnych. Algorytmy genetyczne pozwalają swobodnie eksplorować przestrzeń parametrów PID, a ich operatory krzyżowania i mutacji pomagają unikać utkwienia w minimach lokalnych. Dodatkowo, jeśli użyjemy podejścia wielokryterialnego, możemy uzyskać front Pareto przedstawiający kompromisy między czasem regulacji a przeregulowaniem.
Problem sterowania napędem DC ilustruje, jak teoria optymalizacji przekłada się na bardzo praktyczne, inżynierskie zastosowania — od przemysłu po robotykę mobilną i mechatronikę.
Dobór czynników do modelu predykcyjnego cen energii
W dziedzinie analizy szeregów czasowych jednym z ambitniejszych problemów jest przewidywanie przyszłych cen energii na podstawie danych historycznych. Zakładamy, że dysponujemy rozbudowanym zestawem zmiennych wejściowych: historyczne ceny energii, poziomy produkcji energii (np. z wiatru, fotowoltaiki, gazu), wskaźniki inflacyjne, indeksy giełdowe (np. WIG, S&P500), kursy walut (np. EUR/PLN), notowania surowców (ropa, gaz, węgiel), a także dane pogodowe (temperatura, siła wiatru, nasłonecznienie).
Zadanie polega na znalezieniu najlepszego modelu predykcyjnego (np. regresji liniowej, sieci neuronowej, drzewa decyzyjnego), który na podstawie wybranych zmiennych wejściowych pozwoli możliwie najdokładniej przewidzieć cenę energii w przyszłym kroku czasowym. Istotą problemu jest jednak dobór optymalnego podzbioru czynników wejściowych — nie chcemy używać ich wszystkich, ponieważ:
część może nie wnosić informacji (szum),
część może być redundantna,
większy model oznacza większą złożoność i trudność interpretacji.
Zmiennymi decyzyjnymi są tutaj kombinacje czynników wejściowych — problem ma charakter kombinatoryczny, ponieważ dla potencjalnych zmiennych istnieje możliwych podzbiorów. Dla 20 zmiennych to już ponad milion kombinacji. Dodatkowo, możemy rozważać także wybór typu modelu, hiperparametrów, lagów czasowych — co czyni problem jeszcze bardziej złożonym.
Funkcja celu mierzy jakość predykcji — może to być np. średni błąd bezwzględny (MAE), średni błąd kwadratowy (MSE) lub inna miara dopasowania, obliczana na podstawie danych walidacyjnych. Ponieważ funkcja celu nie ma analitycznego wyrazu i zależy od wyników trenowania modelu, mamy do czynienia z czarną skrzynką, którą można ocenić tylko przez symulację lub eksperyment.
Algorytmy genetyczne są doskonale przystosowane do tego typu problemów. Przestrzeń przeszukiwań to zbiory binarne (czy dany czynnik uwzględniamy), a operatory krzyżowania i mutacji pozwalają dynamicznie eksplorować nowe kombinacje. Warianty permutacyjne i wielokryterialne algorytmów pozwalają uwzględniać równocześnie jakość predykcji i prostotę modelu (np. liczbę zmiennych). Dzięki temu można uzyskać front Pareto modeli — od prostych i umiarkowanie skutecznych, po złożone o bardzo wysokiej trafności.
Ten przykład pokazuje, że optymalizacja nie ogranicza się tylko do „fizycznych” problemów inżynierskich, ale odgrywa coraz większą rolę w eksploracji danych, sztucznej inteligencji i nowoczesnej energetyce.