1.1. Podstawowe zasady modelowania

Model jest reprezentacją określonej rzeczywistości, która pomaga w zrozumieniu tej rzeczywistości. Konkretne przyczyny tworzenia modeli są tak różnorodne jak dziedziny w których modele są stosowane. Modelowanie obecne jest w większości dziedzin działalności człowieka, np. nauce, technice, edukacji czy sztuce. Rysunek 1.1 przedstawia przykłady różnych modeli: model kryształu żelaza zbudowany w powiększeniu, model numeryczny ludzkiego ciała dla potrzeb analizy pola elektromagnetycznego, model nadwozia samochodu oraz model budynku

Rysunek 1.1: Przykładowe modele w różnych dziedzinach

Budowa modeli może mieć różne cele, z których najważniejsze to:

• Testowanie właściwości fizycznych obiektów przed ich wykonaniem.
• Wizualizacja i komunikacja z klientami.
• Redukcja złożoności.

Z punktu widzenia inżynierii oprogramowania najbardziej interesuje nas ten ostatni z wymienionych celów, czyli radzenie sobie ze złożonością otaczającej nas rzeczywistości. Wspomniana wyżej zasada koncentracji na elementach najważniejszych w danym kontekście jest jedną z podstawowych technik stosowanych przez ludzki umysł. Technika ta nazywa się abstrakcją. Żeby ją zastosować, w pierwszej kolejności należy sobie uświadomić jak bardzo istotne są poszczególne charakterystyki modelowanego przez nas w danym momencie tematu z punktu widzenia naszego aktualnego celu. Wyróżniamy zatem cechy danego systemu stosownie do ich wagi, wyróżniając istotne, a odpowiednio mniej eksponując lub wręcz pomijając te o mniejszym znaczeniu. Daje nam to podstawę do zastosowania trzech technik realizujących zasadę abstrakcji, czyli generalizacji, klasyfikacji i enkapsulacji.

Klasyfikacja polega na grupowaniu elementów świata rzeczywistego w kategorie, zgodnie z przyjętymi kryteriami, najczęściej nawiązującymi do jakichś ich wspólnych charakterystyk. Przykłady takiej klasyfikacji został pokazany na rysunku 4.2. Rysunek ten ilustruje również technikę enkapsulacji. Polega ona na grupowaniu elementów w większe całości, które nazywamy i prowadzimy analizę systemu na poziomie tych całości.

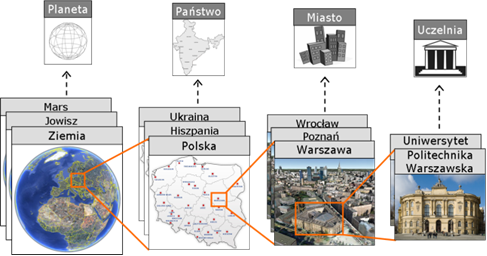
Rysunek 1.2: Przykład zastosowania zasady abstrakcji

Generalizacja polega na tworzeniu pojęć ogólnych poprzez wyodrębnienie pewnego zbioru cech wspólnych dla szeregu pojęć bardziej szczegółowych. Im mniejszy zbiór cech wspólnych, tym bardziej ogólne pojęcie i tym większy zakres konkretnych obiektów, do których pojęcie może być zastosowane. W miarę powiększania zbioru cech wspólnych, pojęcie staje się coraz bardziej szczegółowe, obejmując coraz mniejszy zakres konkretnych obiektów. Generalizacja pozwala tworzyć hierarchię pojęć.

Budując abstrakcyjne modele nie szukamy prawdy absolutnej o otaczającej nas rzeczywistości. Zamiast tego z reguły skupiamy się na wybranym jej fragmencie, który jest najbardziej adekwatny dla celu, jaki przyświeca nam podczas budowy danego modelu. Może zatem istnieć wiele poprawnych, choć mocno różniących się między sobą modeli, które ukazują różne aspekty modelowanego obiektu czy zjawiska.

Oprogramowanie również można potraktować jako model określonego fragmentu świata rzeczywistego. Co ważniejsze jest ono również samo w sobie wysoce skomplikowanym jego elementem. Duże systemy oprogramowania muszą więc odzwierciedlać ogromne ilości obiektów i mechanizmów zachodzących w danym środowisku, które system ma realizować.

Kodowanie w językach programowania nie jest jednak dobrym sposobem modelowania. Często bywa tak, że dana dziedzina nie jest dobrze znana twórcom przystępującym do budowy systemu oprogramowania a wymagania zamawiającego system zmieniają się w trakcie jego realizacji. Trudno byłoby sobie wyobrazić przystąpienie do pisania kodu dużego systemu jedynie na podstawie przekazanego przez zamawiającego, nieformalnego opisu problemu.

Zanim przystąpimy do tego etapu, musimy stworzyć szereg modeli pośrednich, które opisują budowany system oraz jego środowisko z różnych punktów widzenia oraz na różnym poziomie szczegółowości. Wyróżniamy modele struktury, które uwypuklają statyczną budowę systemu, oraz modele zachowania, które opisują aspekty dynamiczne. Modele te mają istotne znaczenie dla właściwego zrozumienia funkcjonalności, jaką system ma zrealizować, jak również pozwalają stworzyć architekturę systemu, którą można elastycznie modyfikować w przypadku zmieniających się wymagań.

Szczegółowe modele projektowe pozwalają stworzenie dobrego, przejrzystego kodu oprogramowania. Model abstrahuje od szczegółów kodu (np. treści metod) i pokazuje np. tylko strukturę powiązań między klasami. Programista może dzięki temu łatwiej zorientować się w strukturze kodu i odpowiedzialności poszczególnych klas.

Dzięki modelowaniu możemy osiągnąć następujące korzyści:

• Zrozumienie celu budowy systemu oraz sposobu jego realizacji,
• Ułatwienie komunikacji pomiędzy twórcami systemu oraz zamawiającym,
• Ułatwienie zarządzania realizacją systemu oraz zarządzanie ryzykiem,
• Ułatwienie dokumentowania systemu.

Modele powinny być podstawowym produktem każdego projektu wytwarzania oprogramowania. Im większy i bardziej złożony system, tym większe znaczenie modelowania.

1.2. Uniwersalny język modelowania

W związku z rosnącą popularnością obiektowych języków programowania zaczęły również pojawiać się obiektowe języki modelowania. W latach 90-tych nastąpił proces unifikacji, co doprowadziło do powstania ujednoliconego języka modelowania – UML (ang. Unified Modelling Language). Twórcami języka byli Grady Booch, James Rumbaugh i Ivar Jacobson, którzy połączyli stosowane wcześniej różne notacje w jeden uniwersalny język. UML jest obecnie najpowszechniej stosowanym językiem modelowania, który jednocześnie został zdefiniowany jako standard (m.in. jako standard ISO/IEC 19505). UML jest językiem graficznym, za pomocą którego można tworzyć modele niezbędne w całym procesie budowy systemu informatycznego. Można go również wykorzystywać do modelowania rzeczywistości niekoniecznie powiązanej z systemem informatycznym. W dalszej części książki będziemy sukcesywnie przedstawiać składnię i semantykę języka UML w wersji 2. Pełną specyfikację języka znaleźć można na stronach internetowych organizacji Object Management Group (www.omg.org), która zajmuje się rozwojem i standaryzacją języka.

1.3. Obiekty jako podstawa modelowania

Jak już wspomnieliśmy, najbardziej rozpowszechnionym współcześnie paradygmatem modelowania jest modelowanie obiektowe. Zgodnie z nazwą, opiera się ono na obiektach, czyli wyodrębnionych elementach rzeczywistości istotnych z perspektywy tworzonego modelu. Każdy obiekt stanowi osobny byt wyraźnie wyodrębniony z całości modelowanej dziedziny. Obiekty mogą zatem reprezentować różnego rodzaju przedmioty, osoby, zdarzenia, procesy lub inne twory niematerialne występujące w danym środowisku.

Z punktu widzenia zamawiającego system, obiekty odpowiadają rzeczywistym elementom modelowanego środowiska (przedmiotom, osobom itd.). Z punktu widzenia programistów, obiekty są podstawowymi jednostkami implementacji oprogramowania w obiektowych językach programowania. Obiekty będące elementami oprogramowania nie zawsze odzwierciedlają w pełni obiekty rzeczywiste z określonego środowiska – często są ich uproszczeniem lub modyfikacją. Ponadto, w systemach oprogramowania występuje szereg dodatkowych obiektów związanych nie ze środowiskiem, lecz z techniczną stroną oprogramowania, jak np. okienka interfejsu użytkownika, formularze wprowadzania danych, interfejsy programistyczne, bazy danych, obiekty sterujące działaniem systemu, itp. Na podstawie obiektów z danej dziedziny świata rzeczywistego, analitycy i projektanci tworzą modele obiektowe, które z kolei są podstawą do stworzenia kodu oprogramowania. Modele te powinny odzwierciedlać różne aspekty modelowanej dziedziny. Możemy zatem określić, że modelowanie obiektowe polega na:

• znajdowaniu interesujących nas konkretnych obiektów w danej dziedzinie,
• opisywaniu struktury i sposobu działania tych obiektów,
• klasyfikacji i generalizacji obiektów,
• znajdowaniu powiązań między nimi,
• opisywaniu dynamicznych aspektów współpracy pomiędzy obiektami.

Zgodnie z paradygmatem obiektowości, obiekt (ang. object) posiada trzy główne cechy: tożsamość, stan i zachowanie.

Zdefiniujmy zatem czym są wspomniane wcześniej trzy cechy obiektu.

Tożsamość (ang. identity) obiektu jest cechą umożliwiającą jego identyfikację i odróżnienie od innych obiektów. Tożsamość jest cechą unikalną wśród wszystkich obiektów i pozostaje niezmienna przez cały czas życia obiektu. W przypadku obiektów w systemie oprogramowania, cechą określająca tożsamość obiektu może być adres obszaru pamięci komputera, w którym dany obiekt się znajduje lub specjalna, ukryta właściwość obiektu, której unikalna wartość jest nadawana automatycznie.

Stan (ang. state) obiektu jest określany przez aktualne wartości wszystkich jego właściwości. Każdy obiekt posiada zbiór właściwości, które go charakteryzują. Zbiór ten nie ulega zmianie przez całe życie obiektu. Zmianie mogą ulegać jedynie wartości tych właściwości. Wartości mogą być np. liczbami, napisami czy innymi obiektami.

Zachowanie (ang. behaviour) obiektu to zbiór usług, które obiekt potrafi wykonać na rzecz innych obiektów. Zachowanie obiektów określa dynamikę systemu – sposób komunikacji pomiędzy obiektami. Efektem wykonania usługi może być jakaś wartość zwracana obiektowi, który poprosił o wykonanie usługi. Wartość ta może zależeć od aktualnego stanu obiektu wykonującego usługę. Podczas wykonywania usługi, obiekt może operować na swoim zbiorze wartości, w wyniku czego może ulec zmianie jego stan.

Język UML dostarcza nam odpowiedniej notacji do reprezentowania obiektów – ich stanu i tożsamości. Przykład tej notacji przedstawia rysunek 1.3. Podstawową ikoną obiektu jest prostokąt zawierający podkreśloną jego nazwę. Po nazwie obiektu można zapisać oddzieloną dwukropkiem nazwę typu (klasy) obiektu (o klasach obiektów będzie mowa w dalszej części rozdziału). W przykładzie na rysunku widzimy np. dwa obiekty o nazwach „Zenek” i „Bogdan”, dla których określony został typ – „Kierowca”. W razie potrzeby możemy również przedstawić aktualny stanu obiektu (w tym również tych właściwości, które określają stan obiektu). Listę właściwości obiektu umieszczamy poniżej jego nazwy. Aktualne wartości poszczególnych właściwości mogą być umieszczone po ich nazwie, oddzielone znakiem „=”. Przykładami obiektów, dla których określono stan są „samochód Zenka” i „samochód Bogdana”.

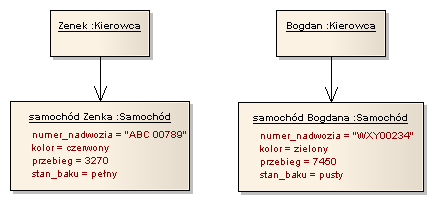
Rysunek 1.3: Notacja dla obiektów w języku UML

Obiekty na diagramie mogą być połączone łącznikami (ang. link), które odzwierciedlają relacje między obiektami. Powiązane obiekty mogą komunikować się między sobą, na przykład poprzez wywoływanie swoich usług. Powiązania mogą być ukierunkowane, wskazując kierunek komunikacji pomiędzy obiektami. Przykładowo, na rysunku 1.3 obiekt „Bogdan” jest powiązany z obiektem „samochód Bogdana”. Kierunek powiązania wskazuje na to, że obiekt „Bogdan” może poprosić obiekt „samochód Bogdana” o wykonanie jakiejś usługi lub poznać jego stan. Odwrotna komunikacja nie jest natomiast dostępna. To, jakie usługi „samochód Bogdana” może wykonać, określa jego zachowanie. Zachowania obiektów nie przedstawia się na diagramach obiektów. Zachowanie jest takie samo dla wszystkich obiektów danej klasy, co omawiamy poniżej.

1.4. Klasy obiektów

Typowe dziedziny problemów składają się z tysięcy czy nawet milionów współistniejących obiektów. Konieczne jest opanowanie tej złożoności. Jak już wiemy, jednym ze sposobów radzenia sobie ze złożonością jest stosowanie zasady abstrakcji poprzez klasyfikację. W modelowaniu obiektowym podstawowym elementem modelowanie nie będzie zatem obiekt, lecz jego uogólnienie, czyli klasa obiektów. Klasa powinna stanowić opis grupy na tyle podobnych obiektów, że z punktu widzenia perspektywy, dla której tworzymy dany model można je potraktować wspólnie.

W skrócie, możemy formalnie zdefiniować klasę w następujący sposób: „Klasa (ang. class) to opis grupy obiektów, które mają taki sam zestaw właściwości oraz sposób zachowania”. Każda klasa ma przypisaną nazwę, która wyróżnia ją spośród innych klas w danym kontekście. Właściwości obiektów reprezentowanych przez klasę zwane są atrybutami (ang. attribute). Klasa może mieć dowolną liczbę atrybutów (w szczególności – nie mieć żadnych atrybutów). Sposób zachowania obiektów danej klasy nazywamy operacjami (ang. operation). Każda operacja określa konkretną usługę, którą obiekty danej klasy mogą wykonywać, np. na rzecz obiektów innych klas. Podobnie jak w przypadku atrybutów, klasa może mieć dowolną liczbę operacji.

Rysunek 1.4 przedstawia przykładowy diagram reprezentujący klasy w języku UML, odpowiadający wcześniej omawianym przykładom. Bardziej szczegółowe objaśnienia języka UML w ogólności, a diagramów klas w szczególności, przedstawiamy w kolejnych rozdziałach. Na razie zwróćmy tylko uwagę, że klasy są reprezentowane poprzez prostokąty opatrzone ich nazwami. Poniżej w odpowiednich przegródkach wymienione są ich atrybuty i operacje. Dodatkowo wszelkie zależności pomiędzy klasami, nazywane ogólnie relacjami, odzwierciedlane są w postaci łączących klas linii. W naszym przykładzie mamy więc klasy reprezentujące samochód i kierowcę połączone odpowiednią relację. Posiadają one zdefiniowane odpowiednie atrybuty i operacje, zgodne z wcześniejszymi przykładami dotyczącymi obiektów.

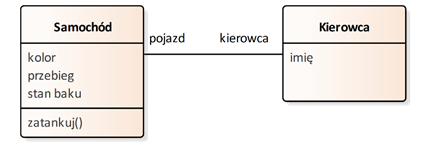
Rysunek 1.4: Przykładowy diagram klas

W języku UML obiekty przypisane do danej klasy, nazywane są instancjami (ang. Instance) klasy. Rysunek 1.5 przedstawia dwa obiekty będące instancjami klasy „Samochód”, na co wskazuje zarówno typ obiektów pokazany w ich nazwie, jak również relacje «instanceOf» łączące obiekty z klasą.

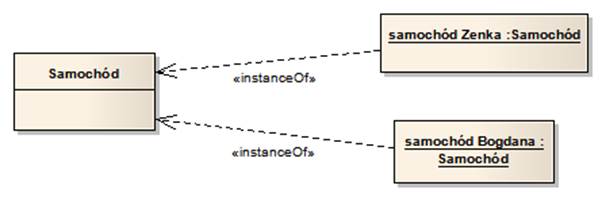
Rysunek 1.5: Obiekty jako instancje klas

Powiedzieliśmy wcześniej, że modele powinny być tworzone z perspektywy konkretnego celu, któremu będą służyć. Różni czytelnicy modeli patrzą na obiekty i ich klasy z różnych perspektyw, w zależności od tego jaką pełnią rolę w procesie tworzenia systemu oprogramowania.

Możemy wyróżnić trzy perspektywy, których można użyć przy tworzeniu modeli, zwłaszcza modeli klas:

Perspektywa pojęciowa. Przyjmując tę perspektywę, modelujemy klasy reprezentujące pojęcia analizowanego środowiska. Model pojęciowy tworzony jest niezależnie od oprogramowania. Zazwyczaj nie ma pełnej odpowiedniości pomiędzy elementami tego modelu a klasami implementacyjnymi.

Perspektywa specyfikacyjna. Perspektywa ta dotyczy bezpośrednio oprogramowania, ale raczej w sensie definiowania typów obiektów niż szczegółów implementacji. Typ może być implementowany przez wiele klas, a klasa może implementować wiele typów. W perspektywie tej unika się zazwyczaj szczegółów związanych z konkretnym językiem programowania czy technologią.

Perspektywa implementacyjna. Perspektywa ta ukazuje wszystkie szczegóły implementacji. Na podstawie modeli implementacyjnych możliwe jest stworzenie kodu oprogramowania.

Wymienione perspektywy nie są formalnie zdefiniowane w języku UML. Są jednak bardzo przydatne podczas tworzenia i analizy modeli, chociaż granice między nimi nie zawsze są jednoznaczne.

1.5. System jako zbiór współpracujących obiektów

Klasy i należące do nich obiekty służą odzwierciedleniu statycznej struktury wybranej dziedziny problemu lub systemu oprogramowania. Obiekty najczęściej nie są jednak bezczynne, lecz wzajemnie na siebie oddziałują. Zbiór współpracujących ze sobą obiektów nazywamy systemem. Oczywistym przykładem systemu jest dowolny system oprogramowania, ale jest to pojęcie znacznie szersze. Działanie każdego systemu – w szczególności systemu oprogramowania – można przedstawić jako wzajemne przesyłanie komunikatów w ramach pewnego zbioru obiektów w ściśle określonym celu. Jak wiemy, obiekty posiadają zachowanie określone przez swoje klasy, w postaci zbioru usług. Usługi te mogą być wykonywane na prośbę innych obiektów. Prośby o wykonanie usługi oraz ewentualne odpowiedzi nazywamy komunikatami (ang. Message). W ramach wykonania usługi, obiekt może operować na wartościach swoich atrybutów, w wyniku czego jego stan może ulec zmianie. Może też przesyłać komunikaty do innych obiektów.

Język UML zawiera szereg różnych diagramów pozwalających odzwierciedlać dynamiczne aspekty modelowanych dziedzin. Przebiegu wymiany komunikatów pomiędzy obiektami możemy przedstawić za pomocą modeli interakcji (ang. Interaction Model). Przykład takiego modelu widzimy na diagramie zamieszczonym na rysunku 1.6. Diagram ten zawiera trzy tzw. linie życia, odpowiadające obiektom przedstawionym na górze diagramu („Bogdan”, „Samochód Bogdana” i nienazwany obiekt klasy „Silnik”). Pomiędzy liniami przebiegają komunikaty wyrażone w formie strzałek. Komunikaty te czytane w kolejności od góry do dołu tworzą sekwencję interakcji między obiektami, w tym wypadku opisującą proces uruchamiania samochodu i rozpoczynania jazdy. W podanym przykładzie kierowca najpierw przesyła do samochodu polecenie, aby się włączył. Powoduje to z kolei przesłanie przez samochód polecenia do silnika, aby się uruchomił. Następnie kierowca rozpoczyna jazdę, czyli wysyła do samochodu polecenie „jedź” (np. w rzeczywistości naciska pedał gazu). Wymaga to zwiększenia obrotów silnika, czyli samochód wysyła odpowiednie polecenie do silnika. Na diagramie widzimy zarówno prośby o wykonanie usługi (pełne strzałki), jak i odpowiedzi oznaczające zakończenie wykonywania usługi przez obiekt (przerywane strzałki).

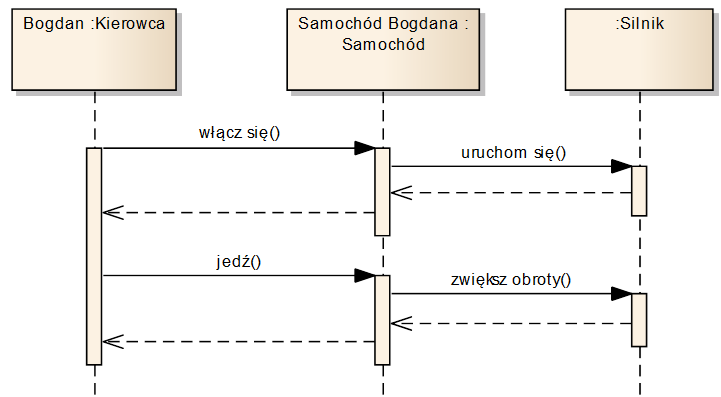
Rysunek 1.6: Przykładowy diagram interakcji

 

Warto zauważyć, że wpływ na to, jak zostanie wykonana określona usługa, mają trzy czynniki.

• Aktualny stan obiektu.
• Parametry komunikatu.
• Stan innych obiektów.

Zauważmy też, że w podanym przykładzie, kierowca chcąc uruchomić silnik, wysyła jedynie odpowiedni komunikat do samochodu i oczekuje na rezultat. Nie wie on, w jaki sposób samochód realizuje usługę „włącz się” i jakie inne obiekty są w to zaangażowane. Samochód jest dla niego czarną skrzynką z przyciskami do wywoływania określonych usług. Można powiedzieć że z punktu widzenia kierowcy uruchomienie samochodu stanowi tzw. proces, jako że znane jest mu tylko jego wejście (co zrobił, żeby go rozpocząć) i wyjście (co uzyskał w jego efekcie). Podejście procesowe jest często przydatne przy wytwarzaniu oprogramowania, jako że dobrze zaprojektowany obiekt udostępnia innym obiektom tylko te usługi lub właściwości, które są im potrzebne. Ważne jest jednak, aby udostępniane usługi (nazwy operacji w klasie) były dobrze i jednoznacznie opisane, tak, aby wywołujący te usługi wiedział co otrzyma w wyniku ich realizacji.