Podręcznik

Język UML oferuje szereg typów modeli służących do modelowania struktury. Różne typy dostosowane są do różnych celów, którym mają służyć. Najbardziej podstawowym i najczęściej używanym typem modelu jest model klas (ang. Class Model). Diagramy klas mogą dotyczyć opisu rzeczywistości, definicji struktur danych lub projektu szczegółowej struktury kodu. Drugim często używanym typem modeli jest model komponentów (ang. Component Model). Model komponentów znajduje zastosowanie przede wszystkim w definiowaniu architektur logicznych systemów oprogramowania. Do modelowania architektur fizycznych służy natomiast model wdrożenia (ang. Deployment Diagram), również nazywany diagramem montażu. Język UML zawiera również inne, rzadziej używane modele służące do modelowania struktury. Są to model obiektów (ang. Object Model), model pakietów (ang. Package Model) oraz model składowych (ang. Composite Structure Model). Ich omówienie wykracza poza zakres tego podręcznika.

2.1. Model klas

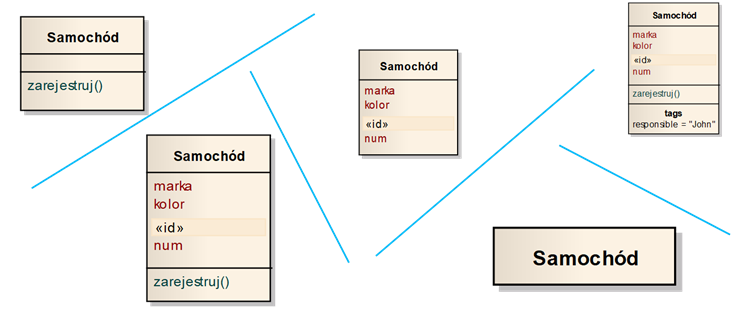
Diagramy klas stanowią najbardziej uniwersalną i prawdopodobnie najbardziej rozpowszechnioną formę modelowania struktury. Podstawowym elementem diagramu klas jest oczywiście klasa, czyli uogólnienie zbioru obiektów o tym samym sposobie zachowania i atrybutach (patrz poprzedni rozdział). Klasa definiuje zatem grupę podobnych obiektów, które zostały uznane za warte wspólnego reprezentowania na potrzeby danego modelu. Na rysunku 2.1 przedstawione zostały różne dopuszczalne reprezentacje graficzne klas w języku UML.

 

Rysunek 2.1: Reprezentacje klas o różnym poziomie szczegółowości

Najprostszą reprezentacją klasy jest prostokąt zawierający wyśrodkowaną nazwę klasy. Ikona klasy może zawierać kilka przegródek, oddzielonych liniami poziomymi. Najczęściej spotykane są reprezentacje składające się z jednej, dwóch lub trzech przegródek. Pierwsza przegródka od góry zawiera nazwę klasy, druga zwiera jej atrybuty, a trzecia – operacje. Język UML dopuszcza tworzenie większej liczby przegródek w zależności od potrzeb. W przykładzie na rysunku 2.1 reprezentacja w prawym górnym rogu zawiera dodatkową przegródkę na tzw. metki (ang. Tag), które określają meta-atrybuty klasy (np. informacje o wersji klasy czy osobie odpowiedzialnej). Na danym diagramie klas, poszczególne przegródki mogą być ujawnione (zwinięte) lub nie.

Przykłady notacji języka UML dla atrybutów przedstawione są na rysunku 2.2. Atrybuty definiują własności opisujące obiekty danej klasy, którym da się przypisać konkretną wartość. Posiadają one konkretne nazwy oraz mogą mieć określny typ. Przykłady notacji języka UML dla operacji widzimy na rysunku 2.3. Operacje reprezentują możliwe sposoby zachowania modelowanych obiektów poprzez określenie możliwych do wykonania funkcji lub procedur. Podobnie jak w przypadku atrybutów, operacje posiadają zdefiniowaną nazwę oraz mogą posiadać typ zwracanego rezultatu. Operacje odróżniane są od atrybutów poprzez podanie parametrów umieszczonych w nawiasach. Dla przykładu, operacja „ObliczCene” na rysunku 2.3 zawiera dwa parametry o nazwach „znizka” oraz „podatek”.

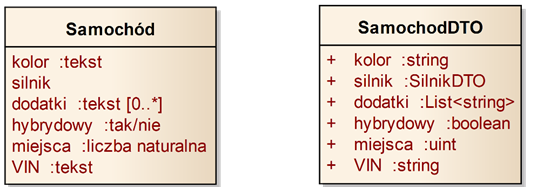
Rysunek 2.2: Przykładowe klasy z pokazanymi atrybutami

Rysunek 2.3: Przykładowe klasy z pokazanymi operacjami

W przykładzie na rysunku 2.2 możemy zauważyć dodatkowe oznaczenie dla jednego z atrybutów – „dodatki”. Oznaczenie to określa tzw. krotność (ang. Multiplicity) lub inaczej – liczność. Krotność dla atrybutów ujmujemy w nawiasy kwadratowe i podajemy jako zakres, np. [1..5] oznacza zakres od 1 do 5. Znak ‘*’ oznacza dowolną wartość, czyli zakres [0..*] oznacza zakres od zera do nieskończoności.

Dodatkowym oznaczeniem składników klasy, używanym najczęściej podczas modelowania kodu, jest widoczność. Widoczność możemy określić zarówno dla atrybutów, jak i operacji. Rodzaje widoczności w języku UML odpowiadają najczęstszym rodzajom widoczności w obiektowych językach programowania.  Widoczność publiczną znakiem ,,+''. Widoczność prywatną oznaczamy znakiem ,,-''.  Widoczność chronioną (ang. protected) oznaczamy znakiem „#”.

Język UML umożliwia również definiowanie własnych typów prostych, za pomocą tak zwanych typów wyliczeniowych (and. enumeration). Umożliwiają one zdefiniowanie typu poprzez określenie listy wartości dla tego typu. Przykładowy typ wyliczeniowy wraz z przykładem jego zastosowania został przedstawiony na rysunku 2.4.

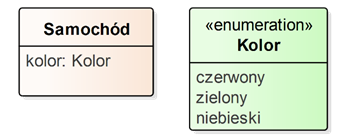
Rysunek 2.4: Przykład typu wyliczeniowego wraz z zastosowaniem

Oznaczenie wykorzystywane w notacji typów wyliczeniowych nosi nazwę stereotypu. Stereotypy możemy nadawać dowolnym elementom języka UML omawianym w tym i kolejnych rozdziałach, czyli w szczególności również klasom. Umożliwiają on nadanie dodatkowego (np. bardziej precyzyjnego) znaczenia danemu elementowi modelu.  W ten sposób możemy tworzyć nowe, własne rodzaje elementów, które pochodzą od elementów standardowych. Szereg istniejących elementów języka UML również używa oznaczenia za pomocą stereotypów. Przykładem są omówione powyżej typy wyliczeniowe oraz interfejsy, które będą omówione w dalszej części rozdziału. Stereotyp jest określany poprzez podanie jego nazwy w nawiasach kątowych (tzw. nawiasy francuskie). Przykłady stereotypów przedstawione są na rysunku 2.5. Stereotyp może być powiązany z określeniem nowego kształtu dla danego elementu modelu. Dla przykładu, na rysunku, stereotypowi «UI Element» został przypisany kształt elementu ekranowego (okienka). Po nadaniu elementowi tego stereotypu, kształt ikony dla tego elementu może się zmienić ze standardowego na przypisany do stereotypu. Zwróćmy zatem uwagę, że mechanizm stereotypów pozwala rozszerzać notację języka UML w sposób praktycznie nieograniczony.

Rysunek 2.5: Przykładowe elementy języka UML z nadanymi stereotypami

Zgodnie z definicją modelowania struktury, diagramy klas, oprócz klas powinny zawierać również różnego rodzaje relacji między klasami. Najczęściej używanymi relacjami na diagramach klas są relacje asocjacji oraz relacje generalizacji. Relacja asocjacji posiada dwa bardziej wyspecjalizowane warianty – relacje agregacji i kompozycji. Często są również stosowane relacje zależności oraz relacje realizacji.

Relacja asocjacji definiuje możliwe powiązania między obiektami klas. Obiekty na końcach asocjacji mogą mieć zdefiniowane określone role. Asocjacje oznaczamy linią łączącą odpowiednie klasy. Role klas możemy zapisać jako nazwy końców asocjacji. Końce asocjacji mogą również definiować krotności dla uczestniczących w relacji obiektów. Krotność określa, ile obiektów danej klasy może potencjalnie być powiązanych z określonym obiektem klasy przeciwnej. Krotności oznaczane są w tej sam sposób jak dla atrybutów (bez nawiasów kwadratowych) – podajemy zakres możliwych wartości. Warto zauważyć, że asocjacja może odzwierciedlać również powiązania między różnymi obiektami tej samej klasy. W takiej sytuacji, asocjacja łączy klasę z samą sobą za pomocą „zawiniętej” linii.

Przykłady asocjacji przedstawia rysunek 2.6. Jak widzimy, między dwoma klasami możemy zdefiniować kilka asocjacji, które określają różne role dla powiązań między obiektami. Dana osoba może występować np. w roli kierowcy lub w roli właściciela dla danego pojazdu. Może również być jednocześnie kierowcą i właścicielem. Zgodnie z diagramem, konkretna osoba może posiadać dowolnie dużo (od 0 do wielu) samochodów oraz może kierować (w danej chwili) maksymalnie jednym samochodem (krotność od zera do jednego). Z kolei samochód może mieć dokładnie jednego właściciela oraz maksymalnie jednego kierowcę. Zwróćmy uwagę na to, że krotność „dokładnie jeden” możemy oznaczyć zarówno jako „1..1” jak i po prostu jako „1”. Ponadto – z założenia – brak określenia krotności dla danego końca asocjacji (lub np. dla atrybutu) oznacza krotność „1”.

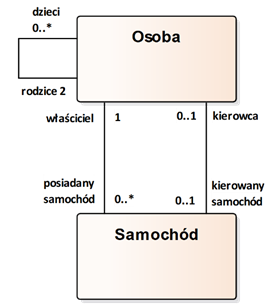
Rysunek 2.6: Przykładowe zastosowania asocjacji

Na rysunku 2.6 widzimy również asocjację dotyczącą tylko klasy „Osoba” (asocjacja „zawinięta”). Zgodnie w tym fragmentem modelu, dana osoba ma dokładnie dwóch rodziców oraz może mieć dowolnie dużo dzieci.

Specjalną własnością asocjacji jest tzw. nawigowalność (skierowanie asocjacji). Nawigowalność oznacza możliwość efektywnego osiągnięcia obiektów jednej klasy przez obiekty drugiej klasy. Inaczej mówiąc, obiekty jednej klasy „wiedzą” o istnieniu odpowiednich obiektów innej klasy i mogą korzystać z ich usług, np. odczytywać ich atrybuty lub uruchamiać ich operacje (dotyczy to tylko elementów o widoczności publicznej). Nawigowalność asocjacji oznaczamy poprzez dodanie grotu strzałki na końcu asocjacji. Zwróćmy uwagę na to, że strzałki możemy umieścić na wszystkich końcach asocjacji, czyli na obydwu końcach w przypadku asocjacji między dwoma klasami. Przy okazji warto wspomnieć, że asocjacje mogą łączyć jednocześnie więcej klas.

Przykład asocjacji nawigowalnej jest przedstawiony na rysunku 2.7. Z rysunku wynika, że obiekty klasy „Dowód rejestracyjny” mają dostęp do danych odpowiadających im samochodów, natomiast obiekty klasy „Samochód” nie mają zdefiniowanego dostępu do danych przypisanych do nich dowodów rejestracyjnych.

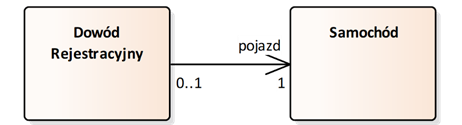
Rysunek 2.7: Przykład asocjacji nawigowalnej

Specjalnym rodzajem asocjacji są relacje agregacji. Stosujemy je, kiedy potrzebne jest odzwierciedlenie związku między grupą, a jej elementem lub elementami. Relacja agregacji jest zatem relacją grupowania, na przykład grupowania składników (części) pewnej całości. Relacja agregacji stosuje wszystkie elementy notacji asocjacji i dodatkowo jest wyróżniana poprzez umieszczenie małej ikony rombu po jednej stronie relacji. Romb umieszczany jest przy tej klasie, która stanowi całość. Przykład relacji agregacji widzimy na rysunku 2.8. Klasa „Samochód” stanowi element grupujący (całość), a klasa „Bagaż” definiuje elementy grupowane (składniki).

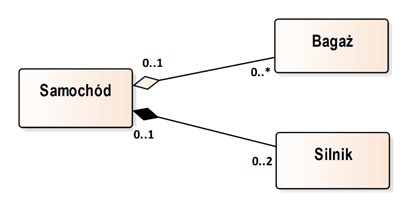
Rysunek 2.8: Przykład zastosowania agregacji i kompozycji

Rysunek 2.8 zawiera również relację między klasami „Samochód” i „Silnik”. Jest ona oznaczona podobnie jak relacja agregacji, lecz ikona rombu jest wypełniona. Jest to relacja kompozycji, która stanowi „silniejszą” wersję relacji agregacji. Reprezentuje ona związek pomiędzy całością a jej integralnymi częściami. Istotną cechą relacji kompozycji jest zasada, że obiekty odpowiadające składnikom nie mogą być zawarte w więcej nić jednym obiekcie odpowiadającym całości. Inaczej mówiąc – w relacji kompozycji składniki nie mogą być dzielone między różne całości. Dlatego też, krotność po stronie całości nie może być większa niż 1. W naszym przykładzie na rysunku 2.8, każdy silnik może być zawarty w co najwyżej 1 samochodzie (ew. może nie być zawarty w żadnym samochodzie). Przy okazji, warto też zwrócić uwagę na krotność po drugiej stronie tej relacji. Wynika z niej, że samochód może posiadać maksymalnie 2 silniki (np. silnik spalinowy i elektryczny). Dodatkowym wyróżnikiem relacji kompozycji jest to, że składniki zazwyczaj powstają i kończą swoje istnienie razem z całością, do której należą – czas życia składników jest ograniczony czasem życia całości (np. silniki samochodu są złomowane razem z samochodem). Ten aspekt relacji kompozycji jest szczególnie istotny podczas modelowania struktury kodu, gdyż definiuje proces tworzenia i destrukcji obiektów składowych. Warto jednak podkreślić, że różnica między relacjami asocjacji, agregacji i kompozycji jest dosyć płynna. Ich stosowanie często zależy od konkretnej dziedziny problemu, kontekstu zastosowania oraz celu danego modelu.

Bardzo ważnym aspektem modelowania obiektowego jest tworzenie taksonomii klas. W obiektowych językach programowania umożliwia to mechanizm dziedziczenia. W języku UML taksonomie tworzymy za pomocą relacji generalizacji-specjalizacji (w skrócie – generalizacji). Relacja generalizacji określa zależność pomiędzy klasami obiektów bardziej ogólnych i klasami obiektów bardziej specjalizowanych. Klasy specjalizowane „dziedziczą” po klasie ogólnej wszystkie jej atrybuty, operacje oraz relacje (asocjacje, agregacje, kompozycje, generalizacje). Oznacza to, że obiekty klasy specjalizowanej posiadają wszystkie elementy zdefiniowane w danej klasie, oraz dodatkowo – wszystkie elementy pochodzące z klasy ogólnej. Język UML dopuszcza również możliwość generalizacji wielobazowej. Klasy mogą zatem specjalizować jednocześnie kilka klas ogólnych. Warto jednak zwrócić uwagę na to, że niektóre języki programowania nie dopuszczają dziedziczenia wielobazowego. W takiej sytuacji należy oczywiście unikać stosowania generalizacji wielobazowej w modelu kodu.

Relacje generalizacji oznaczamy strzałką z dużym grotem w kształcie trójkąta. Strzałka zwrócona jest od klasy specjalizowanej do klasy ogólnej (wskazuje na klasę ogólną). Przykłady zastosowania relacji generalizacji widzimy na rysunku 2.9. Od klasy ogólnej „Pojazd” specjalizują dwie klasy – „Samochód” oraz „Samolot”. Z relacji tych wynika, że obiekty klasy Samochód będą posiadać 4 atrybuty (liczba kół, limit pasażerów, VIN i kolor), a obiekty klasy Samolot – trzy (liczba kół, limit pasażerów, zasięg lotu).

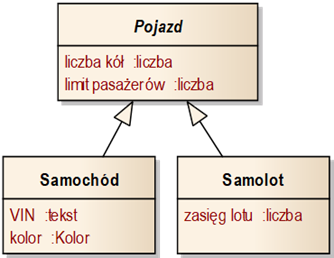
Rysunek 2.9: Przykład zastosowania generalizacji i klas abstrakcyjnych

W relacjach generalizacji często spotykamy klasy na tyle ogólne, że nie posiadają z zasady żadnych obiektów będących ich instancjami. Takie klasy nazywamy klasami abstrakcyjnymi. Używa się ich przede wszystkim w celu przedstawiania cech wspólnych innych klas. Reprezentacja klasy abstrakcyjnej różni się od zwykłej klasy w ten sposób, że jej nazwa zapisana jest kursywą. W przykładzie na rysunku 2.9 klasą abstrakcyjną jest klasa Pojazd. Oznacza to, że w rzeczywistości opisywanej tym diagramem nie istnieją pojazdy jako takie. Konkretny pojazd musi być albo samochodem, albo samolotem, czyli instancją jednej z klas specjalizujących po klasie Pojazd.

Klasy abstrakcyjne stosowane są zarówno w modelowaniu rzeczywistości (modele dziedziny) jak i w modelowaniu kodu. Warto tutaj zwrócić uwagę na to, że w wielu językach programowania istnieją konstrukcje umożliwiające definiowanie klas abstrakcyjnych. Inną konstrukcją używaną podczas programowania, analogiczną do klas abstrakcyjnych jest interfejs. Interfejsy, podobnie jak klasy abstrakcyjne nie posiadają instancji. Zasadniczą rolą interfejsów jest definiowanie zestawów operacji opisujących usługi dostarczane przez określone podsystemy. Stosowanie interfejsów pozwala na oddzielenie specyfikacji funkcjonalności (interfejs) od jej implementacji (konkretna klasa). W odróżnieniu od klas abstrakcyjnych, interfejsy zazwyczaj nie posiadają atrybutów, a jedynie operacje. W języku UML interfejsy modelujemy podobnie jak klasy, przy czym dodatkowo oznaczamy stereotypem «interface». Inną metodą oznaczenia interfejsu jest umieszczenie ikonki ‘○’ (okręgu) w prawym górnym rogu ikony interfejsu.

Notację interfejsów ilustruje rysunek  2.10. Na rysunku, interfejs „IPulaSamochodow” jest implementowany przez klasę „MPulaSamochodow”. Implementacja interfejsu przez klasę w języku UML modelowana jest za pomocą relacji realizacji. Relacja ta jest notacyjnie podobna do relacji generalizacji, przy czym strzałka jest rysowana linią przerywaną. Warto zauważyć, że klasa „MPulaSamochodow” powtarza wszystkie operacje realizowanego interfejsu. W ten sposób wskazujemy, że klasa ta posiada metody (kod wykonawczy) dla odpowiednich operacji interfejsu.

Rysunek 2.10: Przykład interfejsu wraz realizującą go klasą

5.2. Model komponentów i model wdrożenia

Kod systemu oprogramowania może składać się z setek lub nawet tysięcy klas. Czyni to model klas bardzo złożonym i powoduje trudności w zapanowania nad tą złożonością. Najczęściej stosowaną techniką panowania nad złożonymi systemami jest podział całości na mniejsze podsystemy lub komponenty.

Kolejną techniką ułatwiającą panowanie nad złożonością systemów jest stosowanie dobrze określonych interfejsów pomiędzy komponentami. Interfejs definiuje „fasadę” dla komponentu, poprzez którą z danym komponentem komunikują się inne komponenty. Ważne jest to, że wnętrze komponentu zostaje ukryte za fasadą i nie jest dostępne z zewnątrz. Komunikacja poprzez interfejsy pozwala ograniczyć kanały komunikacji wewnątrz systemu. Pozwala to zmniejszyć wzajemne zależności między klasami, które utrudniają diagnozę ewentualnych błędów.

Naszym celem jest ukrycie szczegółów i koncentracja na najważniejszych elementach. Do tego celu możemy wykorzystać model komponentów. Podstawową jednostką modelu komponentów jest komponent, którego notacja w języku UML jest przedstawiona na rysunku 2.11. Komponenty reprezentowane są podobnie do klas, czyli w formie prostokątów z nazwą. Zasadniczo, nie posiadają one jednak dodatkowych przegródek na atrybuty i operacje. Aby odróżnić komponenty od klas oznaczamy je specjalną ikoną w prawym górnym rogu. Na diagramach komponentów umieszczamy komponenty wraz z interfejsami. Interfejsy dostarczane przez komponent oznaczane są specjalną „wypustką” zakończoną okręgiem. Interfejsy wymagane przez komponent różnią się tym, że wypustka zakończona jest półokręgiem. Zwróćmy uwagę na to, że oznaczenia interfejsów na diagramach komponentów wykorzystują analogię wtyczki i kontaktu. Interfejs wymagany i dostarczany można połączyć ze sobą tworząc odpowiednią relację między komponentami.

Rysunek 2.11: Podstawowe elementy notacji komponentu

Łatwo zauważyć, że diagram komponentów ukrywa wiele szczegółów. Jeśli chcemy przedstawić ogólną strukturę systemu, tworzymy diagram komponentów. Jeśli chcemy przedstawić szczegóły struktury poszczególnych komponentów, pokazujemy szczegółowe diagramy klas zawierające definicje interfejsów i klas je realizujących. Oczywiście, na diagramie komponentów możemy uwidaczniać wiele komponentów oraz relacje między nimi. Rysunek 2.12 przedstawia najważniejsze elementy notacyjne dla relacji między komponentami. Relacje najczęściej modelujemy za pomocą relacji zależności (strzałka z przerywaną linią). Najbardziej podstawową metodą jest łączenie interfejsu wymaganego z interfejsem dostarczanym (patrz: „ISystemMagazynowy” na rysunku 2.12). Skróconą metodą zapisu jest pominięcie interfejsu wymaganego i połączenie komponentu zależnością bezpośrednio z interfejsem dostarczanym przez inny komponent (patrz: „IPulaSamochodów”). Jeszcze bardziej zwartą metodą zapisu jest zastosowanie tzw. połączenia montażowego (ang. Assembly). Jest to specjalny rodzaj relacji, którego notacja wykorzystuje połączone notacje interfejsu wymaganego i dostarczanego (patrz: „IZamowienia”). Możliwe jest również połączenie zależnością komponentów w sposób bezpośredni – bez interfejsu. Takie połączenie tworzymy najczęściej wtedy, kiedy komponenty komunikują się w sposób inny niż proceduralny (np. poprzez zapytania SQL). Takie zależności warto wtedy oznaczyć dodatkowym stereotypem (patrz stereotyp «SQL» na rysunku 2.12).

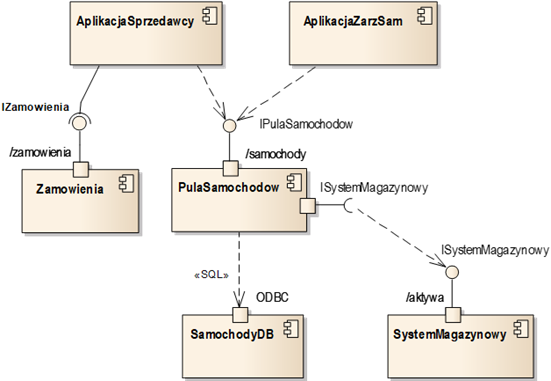
Rysunek 2.12: Przykładowy diagram komponentów

Rysunek 2.12 prezentuje jeszcze jeden istotny element diagramów komponentów – tzw. porty. Port oznacza punkt interakcji komponentu, służący do komunikacji z otoczeniem (np. udostępnieniem usług). Port reprezentowany jest za pomocą małego kwadratu umieszczonego na krawędzi komponentu. Opcjonalna nazwa portu może być umieszczona obok ikony portu. Port może stanowić miejsce powiązania interfejsu z komponentem. Mówimy wtedy, że interfejs jest udostępniany (albo wymagany) poprzez odpowiedni port. Port może mieć różne znaczenie zależne od technologii stosowanej do komunikacji między komponentami. Przykładowo w technologiach stosujących usługi typu REST, port może definiować punkt dostępu (ang. endpoint) z odpowiednim adresem względnym określonym w nazwie portu (patrz np. porty „/samochody” i „/zamówienia” na rysunku 2.12). W technologiach dostępu do relacyjnych baz danych, port może odpowiadać uchwytowi połączenia bazodanowego (np. ODBC).

Model komponentów definiuje ogólną logiczną strukturę systemu. Często jednak konieczne jest również przedstawienie struktury fizycznej, czyli sprzętowej oraz powiązanie jej ze struktura logiczną. Do tego celu wykorzystujemy model wdrożenia, inaczej nazywany modelem montażu (ang. Deplyment Model).  Fizyczne składniki systemu, stanowiące środowisko działania oprogramowania, nazywane są  węzłami (and. Node). Węzłami mogą być na przykład serwery, komputery osobiste, urządzenia mobilne i maszyny wirtualne. Reprezentacją węzłów są prostopadłościany z umieszczoną wewnątrz nazwą. Miedzy węzłami można poprowadzić asocjacje (jak w modelu klas) oznaczające określone ścieżki komunikacyjne. Asocjacje mogą być wyposażone w krotności definiujące możliwe liczby węzłów danego typu. Węzły z relacjami asocjacji zostały zilustrowane na rysunku 2.13. Zgodnie z tym modelem, system powinien obejmować węzeł (np. duża farma serwerów) typu „Klaster SZS” oraz wiele połączonych z nim węzłów typu „Magazyn”, „Sprzedaż”, „Komputer Klienta” i „Smartfon Klienta” (co najmniej 1 dla pierwszych dwóch). Dodatkowo, Klaster SZS łączy się z węzłami typu „Serwer Producenta Samochodów” oraz „Serwer Managzynu”. Zwróćmy uwagę na to, że węzłom (tak jak dowolnym elementom modeli w języku UML) może3my nadawać stereotypy. W naszym przykładzie, stereotypy («kubernetes cluster», «pc computer») doprecyzowują rodzaj węzła z punktu widzenia zastosowanego rozwiązania technologicznego (klaster serwerów w technologii Kubernetes, komputer PC).

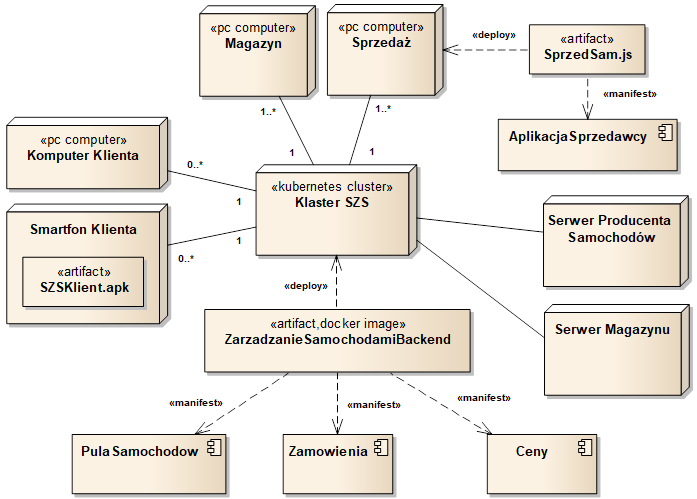
Rysunek 2.13: Przykładowy diagram wdrożenia

Na diagramach wdrożenia możemy również umieszczać tzw. artefakty (ang. Artifact), które reprezentują elementy wykonywane w odpowiednich węzłach. Artefakty najczęściej oznaczają pliki wykonywalne zgodne z konkretną technologią (np. pliki EXE w systemie Windows, pliki APK w systemie Android, pliki JS wykonywane w przeglądarkach internetowych). Notacja dla artefaktów przypomina notację dla komponentów, przy czym wyróżnikiem jest umieszczenie stereotypu «artifact». Artefakty mogą być „montowane” w węzłach. Rysunek 2.13 pokazuje dwa możliwe sposoby zaznaczenia montażu artefaktów. Pierwszy z nich polega na umieszczeniu ikony artefaktu wewnątrz ikony węzła (patrz „SZSKlient.apk”). Drugi polega na zastosowaniu specjalnej relacji zależności (tzw. relacji montażu) oznaczonej stereotypem «deploy» (patrz „SprzedSam.js” i „ZarzadzanieSamochodamiBackend”). Przy okazji zauważmy, że elementy języka UML mogą mieć nadane wiele stereotypów. W naszym przykładzie artefaktowi „ZarzadzanieSamochodamiBackend” nadaliśmy dodatkowy stereotyp «docker image», który sygnalizuje technologię wykonania tego artefaktu (tzw. obraz w technologii Docker).

Artefakty stanowią połączenie modelu fizycznego i logicznego. Modelują one bowiem fizyczne elementy (np. plik), które wyrażają odpowiednie komponenty, czyli składniki logicznej struktury systemu. Na diagramach wdrożenia możemy również pokazać tego typu zależności. Stosujemy w tym celu tzw. relację wyrażania, oznaczaną stereotypem «manifest». Na rysunku 2.13 widzimy kilka takich relacji, które wskazują na komponenty przedstawione w modelu komponentów (por. rysunek 2.12).