Podręcznik

1. Modele neuronów

1.2. Model sigmoidalny neuronu

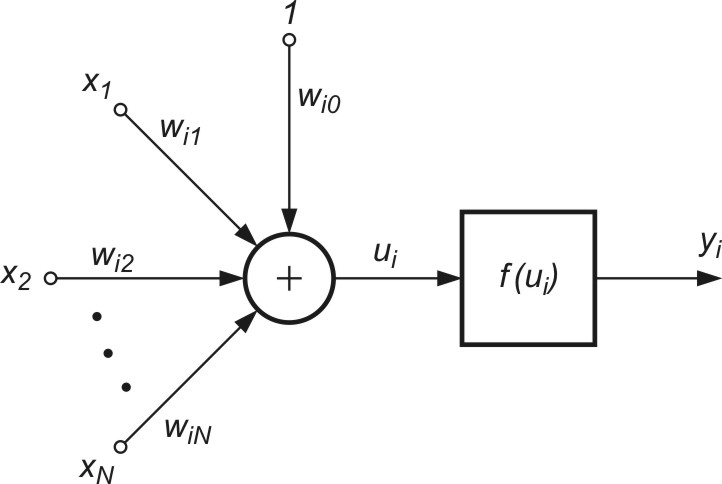
Struktura modelu sigmoidalnego neuronu przedstawiona na rys. 1.1) jest podobna do modelu McCullocha-Pittsa, z tą różnicą, że funkcja aktywacji jest ciągła i przyjmuje postać funkcji sigmoidalnej unipolarnej $f_u(u)$ lub bipolarnej $f_b(u)$ [46]. Funkcje te zapisuje się zwykle w postaci

$f(u) = \frac{1}{1+exp(-bu)}$

(1.2a)

$f_b(u)=tgh(bu)$

(1.2b)

gdzie jest sygnałem sumacyjnym i-tego neuronu, zmienne $x_i$ (i=1, 2, …, N) stanowią składowe wektora x a $x_0$ oznacza sygnał polaryzacji równy zwykle 1 (przy braku polaryzacji równy zeru). Wagi w_ij stanowią wartości połączeń synaptycznych reprezentowane zwykle poprzez wektor $\textbf{w}_i = [ w_{i0}, w_{i1}, \ldots, w_{iN}]^T$ .

Rys. 1.1 Model sigmoidalny neuronu

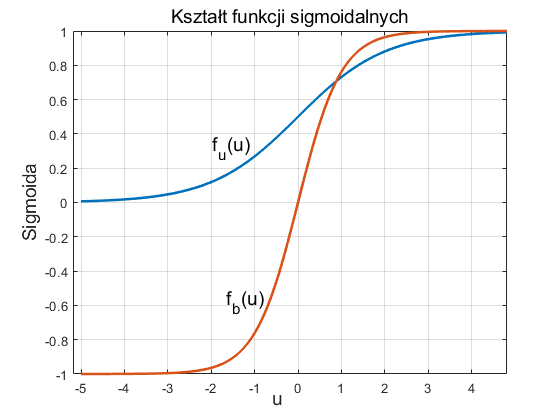
Na rys. 1.2a i 1.2b przedstawiono przebiegi funkcji odpowiednio sigmoidalnej unipolarnej i bipolarnej względem zmiennej $u$ . Przez wprowadzenie bardzo dużej wartości współczynnika $b$ skalującego sygnał sumacyjny $u$ funkcja sigmoidalna może odwzorować funkcję skokową, identyczną z funkcją aktywacji perceptronu McCulocha-Pitsa.

Rys. 1.2 Przebieg funkcji sigmoidalnej: unipolarnej f_u(u) i bipolarnej f_b(u) dla parametru b = 1

Ważną cechą funkcji sigmoidalnej jest jej różniczkowalność. W przypadku funkcji unipolarnej jej pochodna wyraża się wzorem

$\frac{df_u(u)}{du}=b f_u(u)(1-f_u(u))$

(1.3)

natomiast funkcji bipolarnej

$\frac{df_b(u)}{du} = b ( 1-f_b^2(u))$

(1.4)

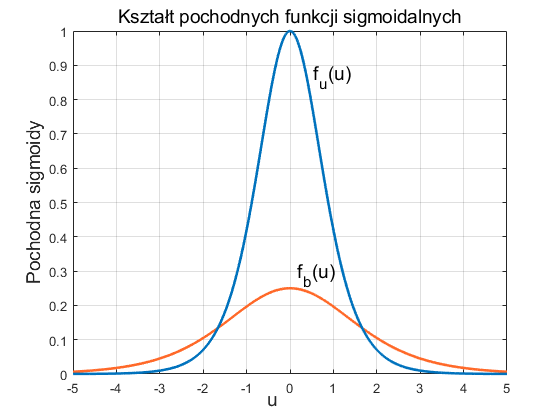
Zauważmy, że dla funkcji sigmoidalnych wartość pochodnej jest całkowicie określona przez wartość samej funkcji. W obu przypadkach wykres zmian pochodnej względem zmiennej u ma kształt krzywej dzwonowej, z maksimum odpowiadającym wartości u=0, jak to przedstawiono na rys. 1.3.

Rys. 1.3 Wykres pochodnej funkcji sigmoidalnej przy b=1

Uczenie neuronu sigmoidalnego odbywa się zwykle w trybie z nauczycielem, przez minimalizację funkcji celu, zwaną również kosztem uczenia, która w przypadku jednej pary uczącej (x, d) definiowana jest dla i-tego neuronu w postaci

$E = \frac{1}{2} ( y_i - d_i)^2$

(1.5)

przy czym aktualny sygnał wyjściowy neuronu określony jest w postaci

$y_i=f(u_i)=f ( \sum_{j=0}^{N} w_{ij}x_j )$

(1.6)

Funkcja $f(u_i)$ jest funkcją sigmoidalną, a $d_i$ wartością zadaną na wyjściu i-tego neuronu. W przypadku zbioru par uczących funkcja celu jest sumą składników dla każdej pary uczącej.

Założenie ciągłej funkcji aktywacji umożliwia zastosowanie w uczeniu metody gradientowej. Najprostszym rozwiązaniem jest zastosowanie metody największego spadku, zgodnie z którą aktualizacja wektora wagowego w odbywa się iteracyjnie z kroku na krok w kierunku ujemnego gradientu funkcji celu

$\textbf{w} (k+1)=\textbf{w}(k)-\eta \frac{\partial E}{\partial \textbf{w}}$

(1.7)

Dla j-tej wagi i-tego neuronu wzór powyższy przyjmie postać

$w_{ij} (k+1)=w_{ij}(k)-\eta \frac{\partial E}{\partial w_{ij}}$

(1.8)

Dla przyjętej definicji funkcji celu E łatwo pokazać, że

$\frac{\partial E}{\partial w_{ij}} = x_j ( y_i -d_i ) \frac{df(u_i)}{du_i}$

(1.9)

Wzór (1.9) w połączeniu z wyrażeniem określającym pochodną funkcji aktywacji definiują algorytm uczenia neuronu sigmoidalnego. Na skuteczność uczenia ma duży wpływ dobór wartości współczynnika uczenia η. W stosowanych rozwiązaniach praktycznych przyjmuje się go bądź to jako wielkość stałą, bądź zmienianą w trakcie uczenia w sposób adaptacyjny. Należy podkreślić, że metoda gradientowa zastosowana w uczeniu neuronu gwarantuje osiągnięcie jedynie minimum lokalnego odpowiadającego wstępnej inicjalizacji wag.

W przypadku funkcji celu wielomodalnej (o wielu minimach lokalnych) znalezione minimum lokalne może być odległe od globalnego. Wyjście ze strefy przyciągania określonego minimum lokalnego nie jest możliwe przy zastosowaniu prostego algorytmu największego spadku. Pewną pomocą może być zastosowanie uczenia z tak zwanym momentem rozpędowym. W metodzie tej proces aktualizacji wag uwzględnia nie tylko informację o gradiencie funkcji, ale również aktualny trend zmian wag. Matematycznie ten sposób uczenia można opisać za pomocą następującego wzoru określającego przyrost wartości wag [24,46]

$\Delta w_{ij} (k+1) = - \eta \frac{\partial E}{\partial w_{ij}} + \alpha \Delta w_{ij} (k)$

(1.10)

w którym pierwszy składnik odpowiada zwykłej metodzie największego spadku, natomiast składnik drugi, zwany składnikiem momentu rozpędowego uwzględnia ostatnią zmianę wag i jest niezależny od aktualnej wartości gradientu. Współczynnik momentu α jest zwykle przyjmowany z zakresu [0, 1] Należy zauważyć, że im większa jest wartość tego współczynnika, tym składnik wynikający z momentu ma większy wpływ na dobór wag. Jego wpływ wzrasta w sposób istotny w pobliżu minimum lokalnego, gdzie wartość gradientu jest bliska zeru. W tym przypadku możliwe są zmiany wag, prowadzące do wzrostu wartości funkcji celu, a więc pokonania bariery ograniczającej minimum lokalne. Ilustracja takiego przypadku przedstawiona jest na rys. 1.4, w zastosowaniu do sieci aproksymującej (spełniającej rolę układu aproksymującego dane wejściowe).

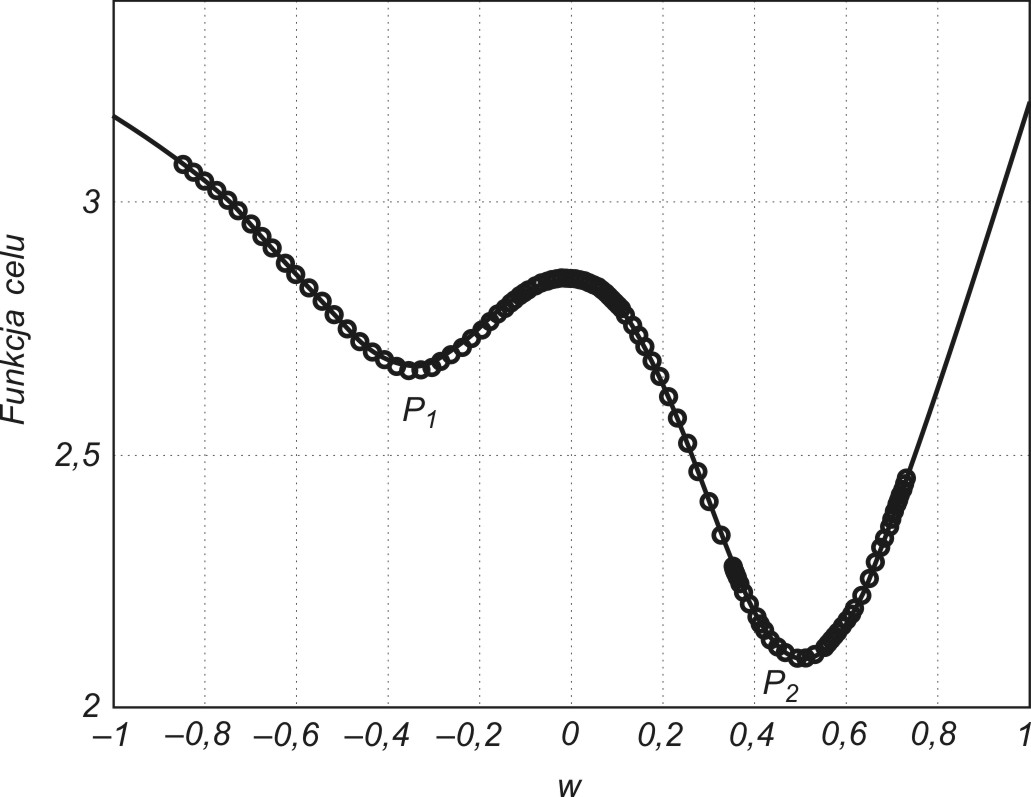
Rys. 1.4 Ilustracja działania momentu rozpędowego

Punkty zaznaczone na wykresie oznaczają wartości funkcji celu uzyskiwane w kolejnych krokach uczących. Minimum lokalne P₁ zostało opuszczone w wyniku działania momentu. Umożliwiło to znalezienie nowego minimum w punkcie P₂ o mniejszej wartości funkcji celu, a więc korzystniejszego ze względu na dopasowanie wartości y_i do wartości zadanej d_i. Należy podkreślić, że czynnik momentu nie może całkowicie zdominować procesu uczenia, gdyż prowadziłoby to do braku stabilizacji algorytmu. Zwykle kontroluje się wartość błędu (y_i-d_i) w procesie uczenia, dopuszczając do jego wzrostu jedynie w ograniczonym zakresie, np. o 5%. W takim przypadku, jeśli wzrost błędu w kolejnym kroku jest mniejszy niż 5% krok jest akceptowany i w efekcie następuje uaktualnienie wartości wag. Jeśli natomiast wartość błędu przekracza założoną wartość 5% zmiany są ignorowane. Przy jednoczesnym założeniu $\Delta w_{ij} (k) = 0$ we wzorze (1.10) składnik gradientowy odzyskuje dominację nad składnikiem momentu zmuszając algorytm do działania zgodnego z klasycznym algorytmem największego spadku.