Podręcznik

1. Modele neuronów

1.4. Model radialny neuronu

Innym rozwiązaniem stosowanym w sieciach neuronowych jest neuron o radialnej funkcji bazowej (aktywacji). Jest to zwykle funkcja typu gaussowskiego, która dla wielkości skalarnych może być opisana wzorem [24]

$\varphi (x) = \exp \left( - \frac{(x-c)^2}{\sigma^2 } \right)$

(1.12)

Wartość funkcji różna od zera występuje jedynie dla zmiennych $x$ w pobliżu centrum $c$ . Wartość parametru $\sigma$ decyduje o szerokości tej funkcji. Przy założeniu, że każdy neuron radialny poddany jest działaniu $N$ sygnałów wejściowych tworzących wektor $\mathbf{x}$ wartość sygnału wyjściowego $y(\mathbf{x})$ tego neuronu można wyrazić wzorem

$\varphi (\textbf {x}) = \exp \| - \frac{(\textbf{x}-\textbf{c})^2}{\sigma^2 } \|$

(1.13)

w którym $\mathbf{x}$ jest $N$ -wymiarowym wektorem wejściowym, podobnie jak wektor centrów $\mathbf{c}$ . Jeżeli weźmiemy pod uwagę, że $\Vert \textbf{x}-\textbf{c} \Vert ^2 =(x_1-c_1)^2 + (x_2-c_2)^2 + ... + (x_N-c_N)^2$ wówczas strukturę szczegółową modelu neuronu radialnego można przedstawić w postaci pokazanej na rys. 1.5.

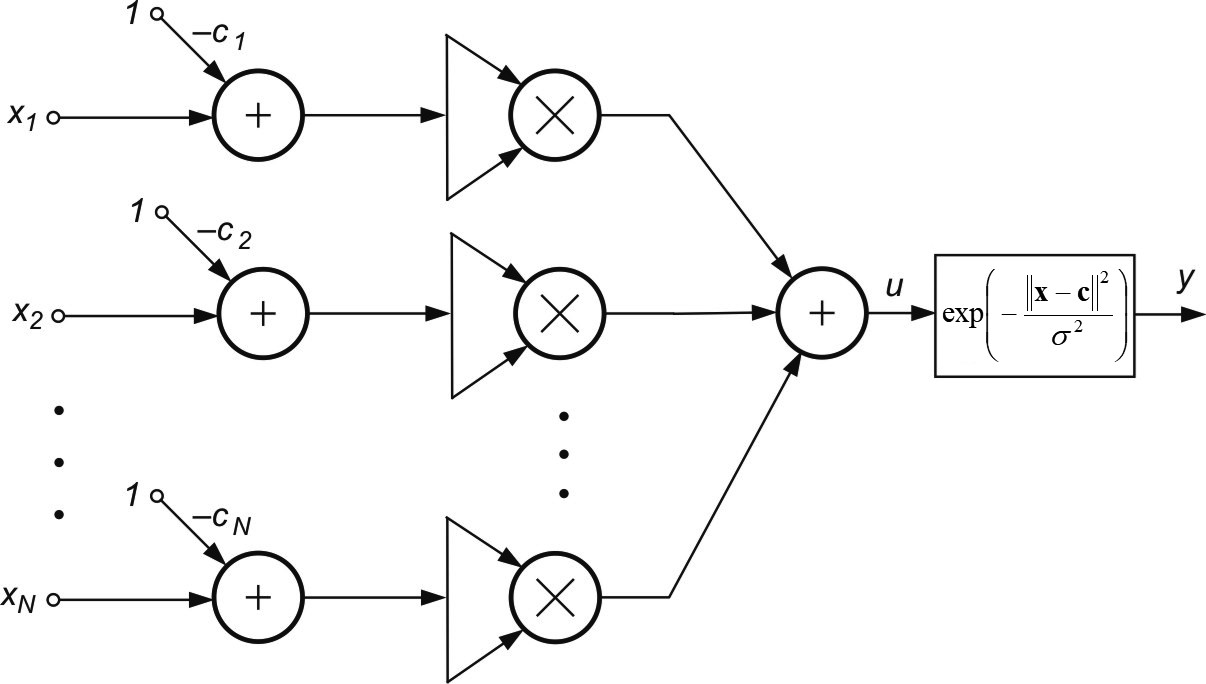
Rys. 1.5 Schemat szczegółowy modelu neuronu radialnego (poprawić wykładnik)

Pomimo pozornego podobieństwa ogólnej postaci neuronu sigmoidalnego i radialnego ich szczegółowe realizacje różnią się znacznie między sobą. Nieliniowość w neuronie radialnym dotyczy wartości sygnału obliczanego nie według zależności liniowej, jak dzieje się to w neuronie sigmoidalnym, ale według zależności nieliniowej (norma euklidesowa wektora).

Uczenie neuronu radialnego polega na doborze wektora centrum i szerokości funkcji radialnej $\sigma$ . Ze względu na lokalny charakter funkcji Gaussa (niezerowa wartość funkcji jedynie w pobliżu centrum) możliwe są tu znaczne uproszczenia, poprzez zastosowanie algorytmu samoorganizacji, adaptującego optymalne położenia centrów dla poszczególnych zmiennych jako środek odpowiedniej grupy danych uczących reprezentowanych przez wektory wejściowe $\mathbf{x}$ .

Najprostszy algorytm samoorganizacji polega na prezentacji wektorów uczących $\mathbf{x}$ i obliczeniu ich odległości od centrów $\mathbf{c}_i$ neuronów (na początku wagi centrów są dobierane losowo). Każdy wektor $\mathbf{x}_i$ jest przypisywany do wektora $\mathbf{c}_i$ najbliższego mu. Zbiór wektorów $\mathbf{x}$ przypisanych do jednego centrum tworzy klaster, dla którego oblicza się nowe centrum będące średnią ze wszystkich wektorów $\mathbf{x}$ przypisanych do niego

$\textbf{c}_i = \sum_{j=1}^{N_i} \textbf{x}_j$

(1.14)

Uaktualnianie wartości wszystkich centrów odbywa się równolegle. Proces prezentacji zbioru wektorów $\mathbf{x}$ oraz uaktualniania wartości centrów powtarzany jest wielokrotnie aż do ustalenia się wartości centrów.

Współczynnik $\sigma$ jest dobierany w taki sposób, aby wartości funkcji radialnych sąsiednich neuronów pokrywały się częściowo ze sobą (dla zapewnienia gładkiego odwzorowania). Często przyjmuje się wartość stałą dla wszystkich neuronów (dla danych znormalizowanych typowa wartość to $\sigma \cong 1$ ).