Podręcznik

2. Sieć perceptronu wielowarstwowego MLP

2.4. Generacja gradientu z użyciem grafów przepływu sygnałów

Algorytm propagacji wstecznej stanowi podstawowy etap w uczeniu gradientowym, gdyż pozwala w prosty sposób określić gradient minimalizowanej funkcji celu. Jest on uważany za jeden ze skuteczniejszych sposobów generacji pochodnej funkcji celu dla sieci wielowarstwowej. W metodzie tej dla uniknięcia bezpośredniego różniczkowania złożonej funkcji celu stosuje się graficzną reprezentację systemu za pomocą grafów przepływowych. Przykład symbolicznej reprezentacji sieci MLP o $N$ wejściach i $M$ neuronach wyjściowych za pomocą grafu przepływowego przedstawiono na rys. 2.2a. W grafie tym wyróżniona została gałąź liniowa o wadze $w_{ij}$ łącząca węzeł o sygnale $v_j$ z węzłem o sygnale $v_i$ oraz gałąź nieliniowa $f(v_l)$ określająca sygnał $v_k=f(v_l)$ , w której $f(v_l)$ w sieci MLP jest funkcją sigmoidalną.

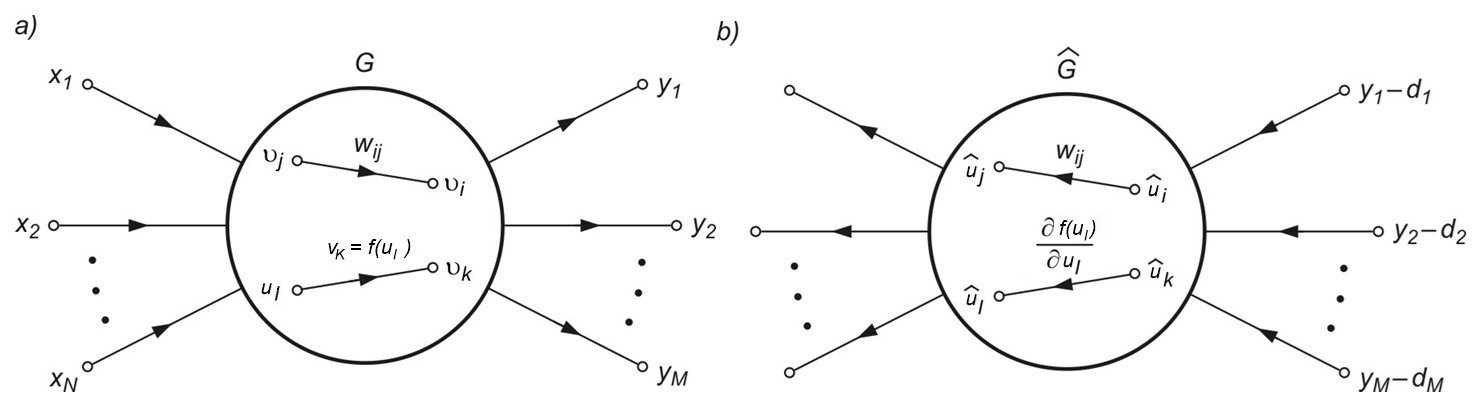
Rys. 2.2 Ogólny schemat reprezentacji sieci MLP za pomocą grafu przepływu sygnałów: a) graf sieci oryginalnej, b) graf dołączony do tej sieci

W generacji gradientu metodą grafów wykorzystuje się zależności odnoszące się do wrażliwości systemu badanego metodą układów dołączonych. Z teorii systemów wiadomo [46], że wrażliwość układu rozumiana jako pochodna dowolnego sygnału w tym układzie względem wartości wag może być określona na podstawie znajomości sygnałów w grafie zwykłym (oznaczonym przez $G$ ) oraz grafie dołączonym (zwanym również grafem sprzężonym) oznaczonym przez $\hat{G}$ . Graf $\hat{G}$ jest zdefiniowany jak oryginalny graf $G$ , w którym kierunki wszystkich gałęzi zostały odwrócone. Opis liniowej gałęzi grafu $G$ i odpowiadającej jej gałęzi grafu dołączonego $\hat{G}$ jest identyczny. W przypadku gałęzi nieliniowej $f(u_l)$ , gdzie $u_l$ jest zmienną wejściową, odpowiadająca jej gałąź grafu $\hat{G}$ staje się gałęzią zlinearyzowaną, o wzmocnieniu równym $\frac{\partial f(u_l)}{u_l}$ obliczonym dla aktualnego punktu pracy nieliniowego grafu $G$ . Graf dołączony reprezentuje więc system zlinearyzowany. Przykład grafu dołączonego $\hat{G}$ do grafu oryginalnego sieci MLP z rys. 2.2a przedstawiono na rys. 2.2b. Dla obliczenia gradientu funkcji celu konieczne jest jeszcze odpowiednie pobudzenie grafu dołączonego.

Jak zostało pokazane, dla określenia gradientu należy sieć dołączoną (graf $\hat{G}$ ) zasilić na zaciskach wyjściowych sieci oryginalnej (obecnie wejściowych) sygnałami wymuszającymi w postaci różnic między wartościami aktualnymi sygnałów wyjściowych $y_i$ a ich wartościami pożądanymi $d_i$ , jak to pokazano na rys. 2.3 b. Przy takim sposobie tworzenia grafu dołączonego każdy składnik wektora gradientu będzie określony na podstawie odpowiednich sygnałów grafu G oraz grafu dołączonego $\hat{G}$ . W odniesieniu do wagi $w_{ij}$ odpowiedni składnik gradientu będzie opisany wzorem

$\frac{\partial E}{\partial w_{ij}} =v_j \hat{v_i}$

(2.6)

w którym sygnał $v_j$ odnosi się do grafu $G$ systemu oryginalnego a $\hat{v_i}$ do grafu $\hat{G}$ systemu dołączonego. Należy podkreślić, że podane zależności odnoszą się do dowolnych systemów (liniowych, nieliniowych, rekurencyjnych itp.). Metodę wyznaczania gradientu zilustrujemy przykładem grafu sieci MLP o 2 wejściach, 2 neuronach ukrytych i dwu neuronach wyjściowych przedstawionym na rys. 2.3a [46].

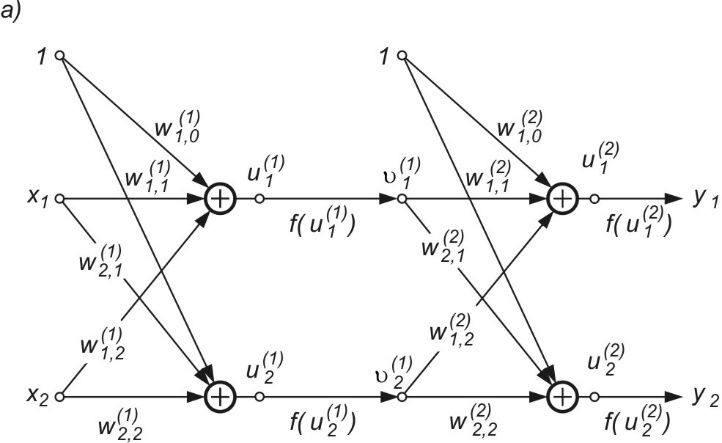
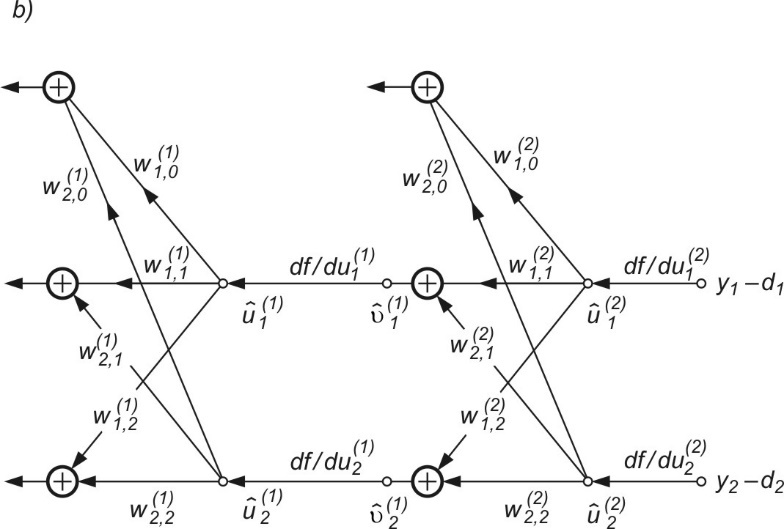
Rys. 2.3 Ilustracja metody grafu dołączonego w zastosowaniu do generacji wektora gradientu dla sieci MLP o 2 wejściach, 2 neuronach ukrytych i 2 neuronach wyjściowych: a) graf wyjściowy sieci, b) graf dołączony reprezentujący propagacje wsteczną.

W celu wyznaczenia wszystkich składników gradientu względem wag poszczególnych warstw sieci wykorzystany zostanie graf dołączony $\hat{G}$ przedstawiony na rys. 2.3b. Pobudzenie grafu dołączonego stanowią różnice między wartościami aktualnymi sygnałów wyjściowych $y_i$ a wartościami zadanymi $d_i$ dla $i=1,2$ . Nieliniowe gałęzie $f(u)$ grafu $G$ zastąpione zostały w grafie dołączonym $\hat{G}$ pochodnymi $\frac{\partial f}{\partial u}$ , obliczonymi odpowiednio w odpowiednich punktach pracy dla każdej warstwy oddzielnie. Zauważmy, że jeśli funkcja aktywacji neuronów ma postać sigmoidalną unipolarną $f(u)=\frac{1}{1+\exp (-u)}$ , wtedy $\frac{\partial f}{\partial u}=f(u)(1-f(u))$ jest określona bezpośrednio na podstawie znajomości wartości funkcji sigmoidalnej w punkcie pracy $u$ i nie wymaga żadnych dodatkowych obliczeń wartości funkcji. Wykorzystując wzór (2.6) można teraz określić poszczególne składowe wektora gradientu $\mathbf{g}=\frac{\partial E}{\partial \mathbf{w}}$ dla dowolnej wagi, zarówno w warstwie ukrytej jak i wyjściowej. Przykładowo

$\frac {\partial E} {\partial w_{12}^{(1)}} =x_2 \hat{u}_1^{(1)}$

$\frac{\partial E}{\partial w_{20}^{(1)}} = \hat{u}_2^{(1)}$

$\frac{\partial E}{\partial w_{11}^{(2)}} =v_1^{(1)} \hat{u}_1^{(2)}$

$\frac{\partial E}{\partial w_{21}^{(2)}} =v_1^{(1)} \hat{u}_2^{(2)}$

Jak wynika z tych sformułowań, ogólna postać wzoru określającego odpowiedni składnik gradientu jest (przy zachowaniu odpowiednich oznaczeń sygnałów) identyczna, niezależnie od tego, w której warstwie neuronów znajduje się odpowiednia waga. Jest to reguła bardzo prosta w zastosowaniach, wymagająca przy określeniu składowej gradientu znajomości tylko dwóch sygnałów: sygnału węzła, z którego waga startuje w grafie zwykłym oraz sygnału węzła, będącego punktem startowym wagi w grafie dołączonym. Pod tym względem stanowi ona regułę lokalną.