Podręcznik
2. Analiza obwodów w stanie ustalonym przy wymuszeniu sinusoidalnym
2.4. Wykres wektorowy obwodu
W przypadku analizy obwodów RLC w stanie ustalonym ważnym pojęciem jest wykres wektorowy, zwany również wykresem wskazowym, przedstawiający w sposób graficzny zależności między poszczególnymi wektorami prądu i napięcia w obwodzie. Jak wiadomo każdej liczbie zespolonej można przyporządkować reprezentację geometryczną w postaci odpowiedniej zależności wektorowej przedstawionej na płaszczyźnie, w której oś pozioma odpowiada części rzeczywistej a oś pionowa części urojonej liczby zespolonej. Konstruując wykres należy pamiętać, że pomnożenie wektora przez operator j jest równoważne obrotowi tego wektora o kąt 90 stopni przeciwnie do ruchu wskazówek zegara gdyż operator j jest równy \(e^{j90^\circ}\). Podobnie pomnożenie wektora przez operator -j jest równoważne jego obrotowi o kąt 90 stopni zgodnie z ruchem wskazówek zegara gdyż operator -j jest równy \(e^{-j90^\circ}\) . Pomnożenie wektora przez liczbę rzeczywistą nie zmienia pozycji wektora w przestrzeni o ile jest to liczba dodatnia lub zmienia zwrot wektora o \(180^o\) jeśli liczba ta jest ujemna.
Z zależności prądowo-napięciowych dla rezystora jest oczywiste, że
| \(U_R=RI_R\) | (2.26) |
co wobec rzeczywistych, dodatnich wartości R oznacza, że napięcie na rezystorze jest w fazie z prądem tego rezystora. Dla cewki obowiązuje
| \(U_L=j\omega LI_L=\omega LI_Le^{j90^o}\) | (2.27) |
co oznacza, że napięcie na cewce wyprzedza prąd o kąt \(90^\circ\). Podobnie napięcie na kondensatorze opóźnia się względem swojego prądu o kąt \(90^\circ\), gdyż
| \(U_C=-j\frac{1}{\omega C}I_C=\frac{1}{\omega C}I_Ce^{-j90^o}\) | (2.28) |
Na rys. 2.3 przedstawiono wykresy wektorowe dla rezystora, cewki i kondensatora z zaznaczeniem przesunięć kątowych między wektorami prądu i napięcia.
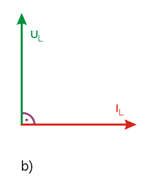
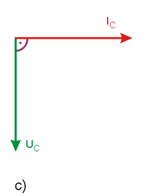
Rys. 2.3. Wykresy wektorowe dla a) rezystora, b) cewki, c) kondensatora
Przedstawione powyżej zasady konstruowania przesunięć kątowych między wektorami prądu i napięcia umożliwiają podanie ogólnych zasad postępowania przy konstruowaniu wykresu wektorowego dla dowolnego połączenia elementów obwodu RLC.
Wykres wektorowy z definicji uwzględnia przede wszystkim przesunięcia kątowe między poszczególnymi wektorami. Relacje ilościowe (długości) poszczególnych wektorów są mniej istotne i zwykle uwzględniane w sposób jedynie przybliżony. Wykres rozpoczyna się zwykle od końca obwodu (gałęzi najdalej położonej od źródła). Jeśli gałąź jest połączeniem szeregowym elementów rozpoczynamy od prądu tej gałęzi, a w przypadku połączenia równoległego – od napięcia. Następnie rysuje się na wykresie na przemian napięcia i prądy kolejnych gałęzi, dochodząc w ten sposób do źródła. Budowę wykresu kończy się w momencie dojścia do prądu i napięcia źródłowego obwodu.
Narysować wykres wektorowy prądów i napięć dla obwodu RLC o strukturze przedstawionej na rys. 2.4.
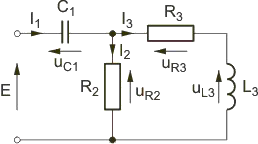
Rys. 2.4. Schemat obwodu RLC do przykładu 2.1
Rozwiązanie
Na rys. 2.5 przedstawiono wykres wektorowy prądów i napięć w obwodzie RLC z rys. 2.4.
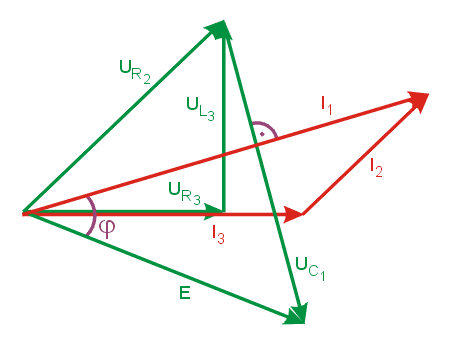
Rys. 2.5. Wykres wektorowy prądów i napięć dla obwodu z rys. 2.4
Sporządzanie wykresu rozpoczyna się od prądu I3 dobudowując wektory napięć i prądów gałęzi przesuwając się w stronę źródła, kolejno: \(U_{R_3},U_{L_3},U_{R_2},I_2,I_1,U_{C_1},E\). Przy założonych wielkościach wektorów obwód ma charakter pojemnościowy, gdyż napięcie wypadkowe E opóźnia się względem odpowiadającego mu prądu \(I_1\).
Położenie wektora prądu źródłowego względem napięcia źródłowego decyduje o charakterze obwodu. Jeśli napięcie wypadkowe (źródłowe) wyprzedza prąd wypadkowy (źródłowy) lub inaczej mówiąc prąd opóźnia się względem napięcia - obwód ma charakter indukcyjny. Jeśli natomiast napięcie opóźnia się względem prądu (lub prąd wyprzedza napięcie) - mówimy o charakterze pojemnościowym obwodu. Jeśli natomiast wektory prądu i napięcia są ze sobą w fazie mówimy, że obwód ma charakter rezystancyjny.