Podręcznik

1. Dany jest zbiór trzech wektorów trójwymiarowych

Określić kąt między poszczególnymi parami wektorów. Jak daleko jest do spełnienia warunku ortogonalności dla każdego przypadku?

2. Funkcja błędu dla sieci neuronowej określona jest wzorem $E=0.2-\mathbf{g}^{\top} \mathbf{w}+0.5 \mathbf{w}^{\top} \mathbf{H} \mathbf{w}$, gdzie

$\mathbf{g}=\left[\begin{array}{l} 0.8 \\ 0.3 \end{array}\right]$, $\quad \mathbf{H}=\left[\begin{array}{cc} 1 & 0,8 \\ 0,8 & 1 \end{array}\right]$.

1. Określić wartość optymalną wektora $\mathbf{w}$ przy której funkcja celu osiągnie swoje minimum.
2. Zastosować metodę największego spadku przy $\eta = 0.3$ oraz $\eta = 1$ dla wyznaczenia tego minimum. 

3. Wygenerować zestaw danych jednowymiarowych typu losowego o rozkładzie gaussowskim należących do dwu klas:

Klasa 1: $\sigma_{1}=1$, $c_{1}=-10$

Klasa 2: $\sigma_{2}=1$, $c_{2}=10$

Zaprojektować klasyfikator MLP separujący te dane. Zilustrować wynik separacji na tle danych. Czy istnieje tylko jedno rozwiązanie teoretyczne? Skomentować wynik.

4. Narysować schemat sieci MLP o 2 wejściach, 3 sigmoidalnych neuronach ukrytych i jednym neuronie wyjściowym (również sigmoidalnym) oraz sieć dołączoną do niej dla generacji gradientu. Napisać wzory na składowe gradientu względem wag sieci.

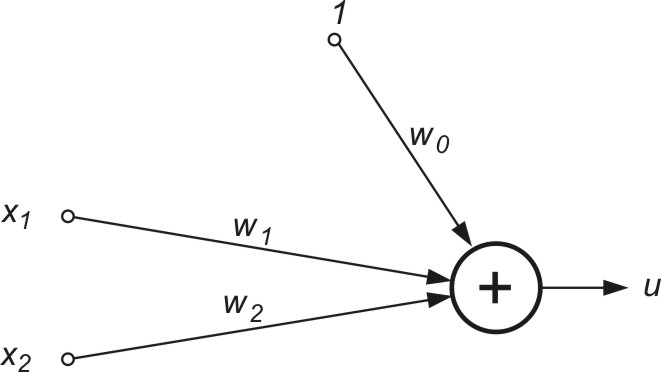
5. Wagi klasyfikatora liniowego 2-wejściowego (rys. 2.12) są znane i równe $w_{0}=-1$, $w_{1}=1.5$, $w_{2}=2$. Na klasyfikator podano 4 wektory $\mathbf{x}$

Określić przynależność tych wektorów do klasy 1 (u>0) lub klasy 2 (u<0). Zilustrować ich przynależność do klas na płaszczyźnie (x₁, x₂). Na podstawie tego rozkładu zaproponować inne wagi klasyfikatora, również rozwiązujące problem separacji obu klas.

 

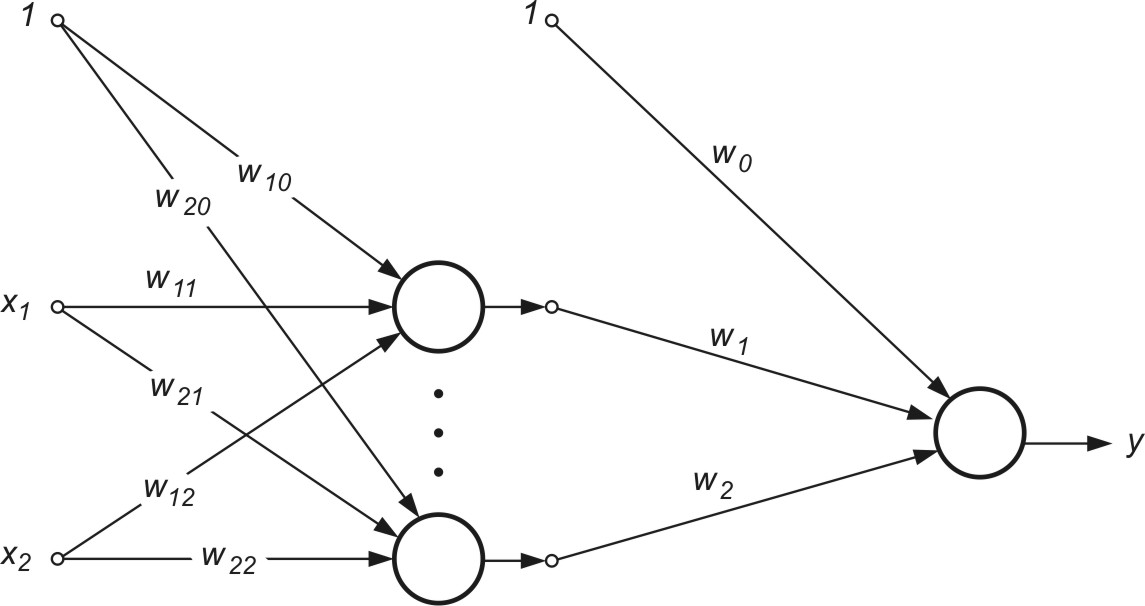
6. Określić przynależność 3 wektorów wejściowych x do jednej z 2 klas przy użyciu sieci MLP o strukturze jak na rys. 2.13.

Przyjąć bipolarną funkcję aktywacji neuronów ukrytych oraz wyjściowych oraz następujące wartości wag: w₁₀=-1, w₁₁=1, w₁₂=1, w₂₀=1, w₂₁=2, w₂₂=4, w₀=-1, w₁=1, w₂=1.

7. Sieć neuronowa jednowyjściowa realizuje następującą funkcję aproksymacyjną

$y(x)=f\left(w_1 f\left(w_{11} x_1+w_{12} x_2\right)+w_2 f\left(w_{21} x_1+w_{22} x_2\right)\right)$

w której $f()$ reprezentuje funkcję sigmoidalną unipolarną. 

Zakładając wartości startowe wag sieci: $w_1=-0.2; w_2=0.1; w_{11}=-0.3; w_{12}=0.5; w_{21}=1; w_{22}=-0.7$ określić gradient i hesjan funkcji celu dla jednej pary uczącej równej $(\mathbf{w}, d)$, gdzie $\mathbf{x}=[1 \; 2]^T$, $d=0.5$.

8. Dla danych z poprzedniego zadania wyznaczyć kierunek minimalizacji odpowiadający metodzie największego spadku oraz klasycznej metodzie Newtona (wzór 2.14). Sprawdzić czy zastosowanie metody newtonowskiej prowadzi w danych warunkach do minimum funkcji celu.