Podręcznik
3. Zdolności generalizacyjne sieci neuronowych
3.2. Miara VCdim i jej związek z generalizacją
Problem optymalnego uczenia sieci polega na wyselekcjonowaniu struktury sieci i doboru jej parametrów w taki sposób, aby aproksymować wartości zadane \( \mathbf{d}(\mathbf{x}_k) \) dla \( k=1,2,\ldots,p \) z minimalnym błędem, i optymalnością definiowaną w sensie statystycznym. W teorii optymalnego uczenia kluczową rolę odgrywa pojęcie miary Vapnika-Chervonenkisa (VCdim), zdefiniowane dla sieci realizującej funkcję klasyfikatora.
Miara VCdim została zdefiniowana dla sieci klasyfikacyjnej jako liczebność \( n \) największego zbioru danych wzorców, dla których system może zrealizować wszystkie możliwe \( 2^n \) dychotomii tego zbioru (podział zbioru na dwie części za pomocą linii prostej). VCdim jest miarą pojemności lub zdolności sieci do realizacji funkcji klasyfikacyjnej wzorców. Miara VCdim odgrywa istotną rolę przy określaniu minimalnej liczby danych uczących \( p \), gdyż dla uzyskania dobrej generalizacji powinien być spełniony warunek \( p \gg VCdim \).
Zostało dowiedzione, że dla sieci jednowarstwowej o jednym neuronie wyjściowym i \( N \) wejściach miara \(VCdim \) jest równa \( N+1 \), czyli równa liczbie połączeń wagowych z uwzględnieniem polaryzacji. Dla sieci jednowyjściowej (jeden neuron wyjściowy) zawierającej jedną warstwę ukrytą i skokowej funkcji aktywacji neuronów miara \(VCdim \) jest równa także \( N+1 \). Dla sieci o dowolnej liczbie warstw ukrytych i skokowej funkcji aktywacji miara \(VCdim \) jest proporcjonalna do \( n_w \lg (n_w) \), gdzie \( n_w \) jest całkowitą liczbą wag sieci. Zastosowanie sigmoidalnej funkcji aktywacji zwiększa tę miarę do wartości proporcjonalnej do \( n_w^2 \). Dla porównania, w sieci liniowej o liczbie wag \( n_w \) miara \(VCdim \) jest proporcjonalna do liczby wag. Jak z powyższego widać niezależnie od zastosowanej funkcji aktywacji neuronów w sieci MLP miara \(VCdim \) jest zawsze skończona i uzależniona od liczby wag.
Jeżeli przez \( P_u \) oznaczymy prawdopodobieństwo wystąpienia błędu na zbiorze danych uczących (względny błąd klasyfikacji dla danych uczących) a przez \( P_t \) - prawdopodobieństwo wystąpienia błędnej klasyfikacji w przyszłym użytkowaniu sieci na danych nie uczestniczących w uczeniu (testowanie) to istotnym problemem jest oszacowanie spodziewanego błędu na tych danych, zwłaszcza jego górnej granicy. Zostało udowodnione, że prawdopodobieństwo wystąpienia błędu testowania większego o wartość \( \varepsilon \) od błędu uczenia dla sieci MLP jest określone wzorem [24,68]
| \( P\left\{\sup _{\mathbf{w}}\left|P_t(\mathbf{w})-P_u(\mathbf{w})\right| \geq \varepsilon\right\} \leq\left(\frac{2 e p}{h}\right)^h e^{-\varepsilon^2 p} \) | (3.1) |
w którym \( P \) oznacza prawdopodobieństwo, \( P_t \) i \( P_u \) – prawdopodobieństwo popełnienia błędu klasyfikacyjnego (przez sieć o wagach określonych wektorem \( \mathbf{w} \) na danych odpowiednio testujących i uczących, \( p \) - liczbę danych uczących, \( e \) - podstawę logarytmu naturalnego a \( h \) - aktualne oszacowanie miary \( VCdim \). Funkcja wykładnicza \( e^{-\varepsilon^2 p} \) ![]() wskazuje, że wraz ze wzrostem liczby danych uczących prawdopodobieństwo wystąpienia błędu klasyfikacji ma niższą wartość ograniczenia górnego. Przy skończonej wartości \( h \) i liczbie wzorców uczących dążącej do nieskończoności prawdopodobieństwo popełnienia tego błędu dąży do zera. Jeśli przez \( \alpha \) oznaczymy prawdopodobieństwo wystąpienia zdarzenia \( \alpha=P\left(\sup \left|P_t(\mathbf{w})-P_u(\mathbf{w})\right| \geq \varepsilon\right) \) wtedy z prawdopodobieństwem \( 1 - \alpha \) można stwierdzić, że \( P_t \le P_u + \varepsilon \). Na podstawie tych zależności otrzymuje się
wskazuje, że wraz ze wzrostem liczby danych uczących prawdopodobieństwo wystąpienia błędu klasyfikacji ma niższą wartość ograniczenia górnego. Przy skończonej wartości \( h \) i liczbie wzorców uczących dążącej do nieskończoności prawdopodobieństwo popełnienia tego błędu dąży do zera. Jeśli przez \( \alpha \) oznaczymy prawdopodobieństwo wystąpienia zdarzenia \( \alpha=P\left(\sup \left|P_t(\mathbf{w})-P_u(\mathbf{w})\right| \geq \varepsilon\right) \) wtedy z prawdopodobieństwem \( 1 - \alpha \) można stwierdzić, że \( P_t \le P_u + \varepsilon \). Na podstawie tych zależności otrzymuje się
| \( \alpha=\left(\frac{2 e p}{h}\right)^h \exp \left(-p \varepsilon^2\right) \) | (3.2) |
Wprowadźmy oznaczenie \( \varepsilon_0(p, h, \alpha) \)
| \( \varepsilon_0(p, h, \alpha)=\sqrt{\frac{h}{p}\left[\lg \left(\frac{2 p}{h}\right)+1\right]-\frac{1}{p} \lg (\alpha)} \) | (3.3) |
Wartość \( \varepsilon_0(p, h, \alpha) \) określa przedział ufności odpowiadający prawdopodobieństwu \( \alpha \) na zbiorze danych uczących przy \( p \) danych i aktualnej mierze \( VCdim=h \). Oszacowanie \( P_t \le P_u + \varepsilon \) odpowiada najgorszemu przypadkowi. Przy małej wymaganej w praktyce wartości \( P_t \) oszacowanie powyższe można znacznie uściślić. W takim przypadku z prawdopodobieństwem \( (1-\alpha) \) można stwierdzić, że [24]
| \( P_t \leq P_u+\varepsilon_1\left(p, h, \alpha, P_u\right) \) | (3.4) |
gdzie
| \( \varepsilon_1\left(p, h, \alpha, P_u\right)=2 \varepsilon_0^2(p, h, \alpha)\left(1+\sqrt{1+\frac{P_u}{\varepsilon^2(p, h, \alpha)}}\right) \) | (3.5) |
W tym przypadku przedział ufności zależy również od błędu uczenia \( P_u \). Przy pomijalnej wartości błędu uczenia \( P_u \) wartość \( \varepsilon_1 \) upraszcza się do wyrażenia
| \( \varepsilon_1(p, h, \alpha)=4 \varepsilon_0^2(p, h, \alpha) \) | (3.6) |
w której przedział ufności \( \varepsilon_0 \) określony jest zależnością (3.3) i jest funkcją jedynie parametrów \( p, h, \alpha \). W świetle teorii generalizacji można stwierdzić, że z prawdopodobieństwem \( (1-\alpha) \) przy liczbie danych uczących \( p>h \) (\( h \) – aktualna wartość miary \( VCdim\) ) błąd generalizacji będzie mniejszy niż wartość gwarantowana \( P_g \) określona wzorem
\( P_g=P_u+\varepsilon_1\left(p, h, \alpha, P_u\right) \),
w którym wartość \( \varepsilon_1 \) jest w ogólności zdefiniowana zależnością (3.5), lub przy bardzo małej wartości błędu uczenia \( P_u \) wzorem (3.6).
Na rys. 3.1 przedstawiono typowe zależności błędu uczenia, gwarantowanego ograniczenia górnego błędu generalizacji oraz przedziału ufności w funkcji miary VCdim.
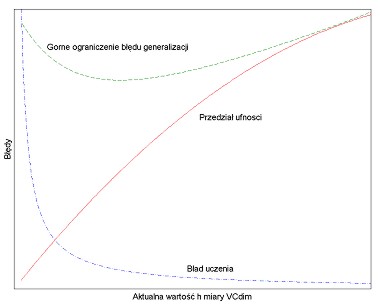
Dla wartości \( h \) mniejszej niż wartość optymalna \( h_{opt} \) pojemność sieci jest zbyt mała dla prawidłowego odwzorowania szczegółów danych uczących i stąd górne ograniczenie błędu generalizacji jest na wysokim poziomie. Dla \( h > h_{opt} \) jest ona z kolei zbyt duża i dlatego błąd generalizacji również rośnie. Osiągnięcie punktu optymalnego (minimum błędu generalizacji) wymaga zwykle trenowania wielu sieci i wybrania tej, która zapewnia otrzymanie minimum gwarantowanego błędu.
Z wartością miary \( VCdim \) oraz zadanym poziomem ufności \( \varepsilon \) odpowiadającym prawdopodobieństwu \( \alpha \) związana jest reguła doboru liczby wzorców uczących wystarczających do uzyskania żądanej dokładności. Zgodnie z pracą [68] liczba próbek uczących powinna spełniać warunek
| \( p \geq \frac{A}{\varepsilon}[h \lg (1 / \varepsilon)+\lg (1 / \alpha)] \) | (3.7) |
gdzie \( A \) jest bliżej nieokreśloną stałą. Z zależności powyższej widać, że liczba próbek uczących powinna być wielokrotnością miary \( VCdim \) (określonej w tym wzorze symbolem \( h \)) i powinna wzrastać wraz ze zmniejszaniem się przedziału ufności. Według opinii Vapnika w klasycznym uczeniu sieci neuronowych dobrą generalizację obserwuje się, jeśli liczba danych uczących jest co najmniej 20 razy większa niż miara \( \mathbf{VCdim} \). Z drugiej strony należy zaznaczyć, że w wielu przypadkach można uzyskać dobre zdolności generalizacyjne sieci MLP przy dalece niewystarczającej liczbie danych uczących [68]. Świadczy to o skomplikowanym mechanizmie generalizacji i naszej niewystarczającej wiedzy teoretycznej w tym zakresie. Stąd wyprowadzone wcześniej oszacowania należy traktować jako ogólną wskazówkę postępowania przy budowie struktury sieci, zmuszającą do maksymalnej redukcji jej stopnia złożoności, przy zapewnieniu akceptowalnego poziomu błędu uczenia.