Podręcznik

Rozważania teoretyczne przedstawione w poprzednim punkcie pokazały ścisły związek zdolności generalizacyjnych sieci MLP z liczbą wag wyrażoną poprzez miarę $VCdim$. Dla uzyskania dobrej generalizacji sieci należy minimalizować liczbę wag do pewnej granicy określonej wymaganiami dotyczącymi błędu uczenia.

W praktyce minimalizację struktury sieci przeprowadza się w pierwszym etapie projektowania przez wielokrotne powtarzanie procesu uczenia na różnych strukturach i wybranie tej, która przy zadowalającym poziomie błędu uczenia pozwala uzyskać najmniejszy błąd odtwarzania danych nie uczestniczących w uczeniu. W następnych etapach projektowania sieci optymalnej poprawę generalizacji można uzyskać przez obcinanie wag najmniej znaczących, czyli wag o najmniejszej wartości bezwzględnej bądź wag o najmniejszym wpływie na wartość funkcji błędu, (niekoniecznie najmniejszych).

Redukcję wag i neuronów osiągnąć można różnymi metodami, z których najbardziej skuteczne opierają się na wykorzystaniu metod wrażliwościowych pierwszego lub drugiego rzędu (np. OBD, OBS) bądź też zastosowaniu w uczeniu metod funkcji kary, karzących za nadmierną liczbę połączeń wagowych. Ten kierunek działania polega na dodaniu do konwencjonalnej definicji funkcji celu składników proporcjonalnych do liczby i wartości wag sieci. W procesie optymalizacji funkcji celu minimalizacji podlegają wówczas również wartości wag sieci. Po zakończeniu procesu uczenia wagi najmniejsze są obcinane i w ten sposób złożoność sieci również ulega redukcji.

Techniką która umożliwia polepszenie zdolności generalizacyjnych sieci jest również wtrącanie szumu do próbek uczących, upodobniające warunki uczenia do warunków przyszłego użytkowania. Istotą tego podejścia jest założenie, że podobne sygnały wejściowe powinny generować podobne odpowiedzi (zasada ciągłości), nawet wtedy, gdy nie wchodziły w skład wektorów uczących. Zbiór uczący wzbogaca się o dane, będące "zaszumioną" wersją sygnałów oryginalnych (przy tych samych wartościach zadanych) i trenuje sieć na rozszerzonym zbiorze danych. Zostało udowodnione, że taki sposób uczenia odpowiada w efekcie minimalizacji funkcji celu zmodyfikowanej o czynnik modelujący wrażliwość względną sieci, odpowiadającą zmianom wartości odpowiedzi neuronów wyjściowych spowodowanych zmianami wartości zmiennych wejściowych (zmiana upodobniająca warunki uczenia do warunków testowania na danych nie biorących udziału w uczeniu sieci).

Zwiększenie efektywności działania sieci uzyskać można poprzez stosowanie wielu sieci neuronowych na raz, tzw. zespół sieci. Technika ta może być zastosowana w każdym trybie działania sieci, w tym w trybie aproksymacji (regresji) jak i w trybie klasyfikacyjnym. Istotą metody jest zastosowanie wielu sieci rozwiązujących na raz ten sam problem. Końcowy wynik może być ustalony na wiele sposobów: głosowanie w przypadku klasyfikacji bądź różnego rodzaju uśrednianie w przypadku aproksymacji. Warunkiem poprawnego działania zespołu jest zastosowanie jednostek o niezależnym działaniu. Można to osiągnąć stosując między innymi różne rozwiązania klasyfikatorów, zróżnicowane zbiory uczące bądź zastosowanie różnych metod przekształcenia danych pomiarowych na cechy diagnostyczne procesu.

Innym problemem jest wpływ sposobu i czasu uczenia na zdolności generalizacyjne sieci. Jak zostało zaobserwowane na przykładzie wielu eksperymentów numerycznych wraz z upływem czasu błąd uczenia maleje i błąd testowania również (przy ustalonej liczbie próbek uczących p oraz wartości miary VCdim). Taka sytuacja trwa zwykle do pewnego momentu uczenia, poczynając od którego błąd testowania pozostaje stały bądź zaczyna rosnąć, pomimo, że błąd uczenia nadal nieznacznie maleje [68].

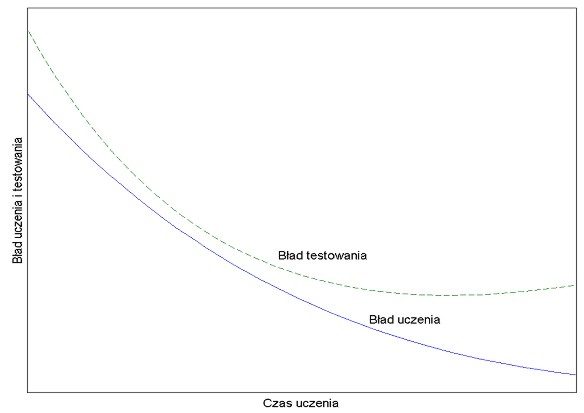
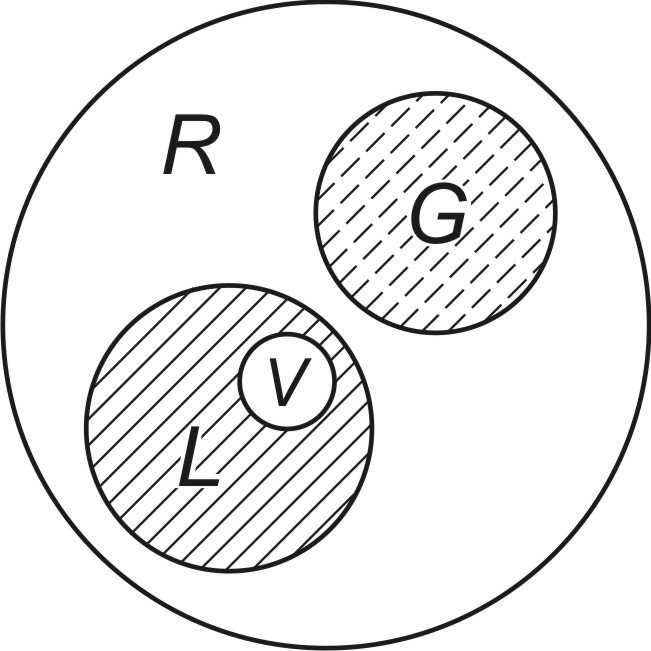
Typowy przebieg obu błędów przedstawiono na rys. 3.2, na którym błąd uczenia zaznaczony jest linią ciągłą, a błąd generalizacji (testowania) linią przerywaną. Z wykresu na rysunku wynika jednoznacznie, że zbyt długie uczenie może doprowadzić do tak zwanego ,,przeuczenia" sieci, a więc do zbyt drobiazgowego dopasowania wag do nieistotnych szczegółów danych uczących. Taka sytuacja ma miejsce w przypadku sieci o nadmiarowej w stosunku do potrzeb liczbie wag i jest tym bardziej widoczna, im większa nadmiarowość wag występuje w sieci. Wagi ,,niepotrzebne" dopasowują się do wszelkich nieregularności danych uczących, traktując je jako cechę główną. W procesie testowania sieci na danych testujących, w którym brakuje tych nieregularności, powstają w efekcie dodatkowe błędy odtwarzania. W celu uniknięcia przeuczenia wydziela się ze zbioru uczącego część danych weryfikujących (zbiór V na rys. 3.3), które służą w procesie uczenia okresowemu sprawdzaniu aktualnie nabytych zdolności generalizacyjnych. Uczenie przerywa się, gdy błąd generalizacji na tym zbiorze osiągnie wartość minimalną (zaczyna wzrastać). Zalecane proporcje danych uczących do weryfikujących to 4:1.

Z uwagi na błąd generalizacji ważny jest stosunek liczby próbek uczących do liczby wag sieci. Mała liczba próbek uczących przy ustalonej liczbie wag oznacza dobre dopasowanie sieci do próbek uczących, ale złą generalizację, gdyż w procesie uczenia nastąpił nadmiar parametrów dobieranych (wag) względem dopasowywanych do siebie wartości zadanych i aktualnych sygnałów wyjściowych sieci. Parametry te zostały zbyt precyzyjnie, a przy tym wobec nadmiarowości wag w sposób niekontrolowany poza punktami dopasowania, dobrane do konkretnych danych, a nie do zadania, które miało być reprezentowane przez te dane uczące. Zadanie aproksymacji zostało niejako sprowadzone do zadania bliższego interpolacji. W efekcie, wszelkiego rodzaju nieregularności danych uczących spowodowane przez przypadkowe zmiany i szumy pomiarowe mogą być odtworzone jako cecha podstawowa procesu. Funkcja, odwzorowana w zadanych punktach uczących jest dobrze odtwarzana tylko dla nich. Minimalne nawet odejście od tych punktów powoduje znaczny wzrost błędu, co przejawia się jako błąd generalizacji.

  

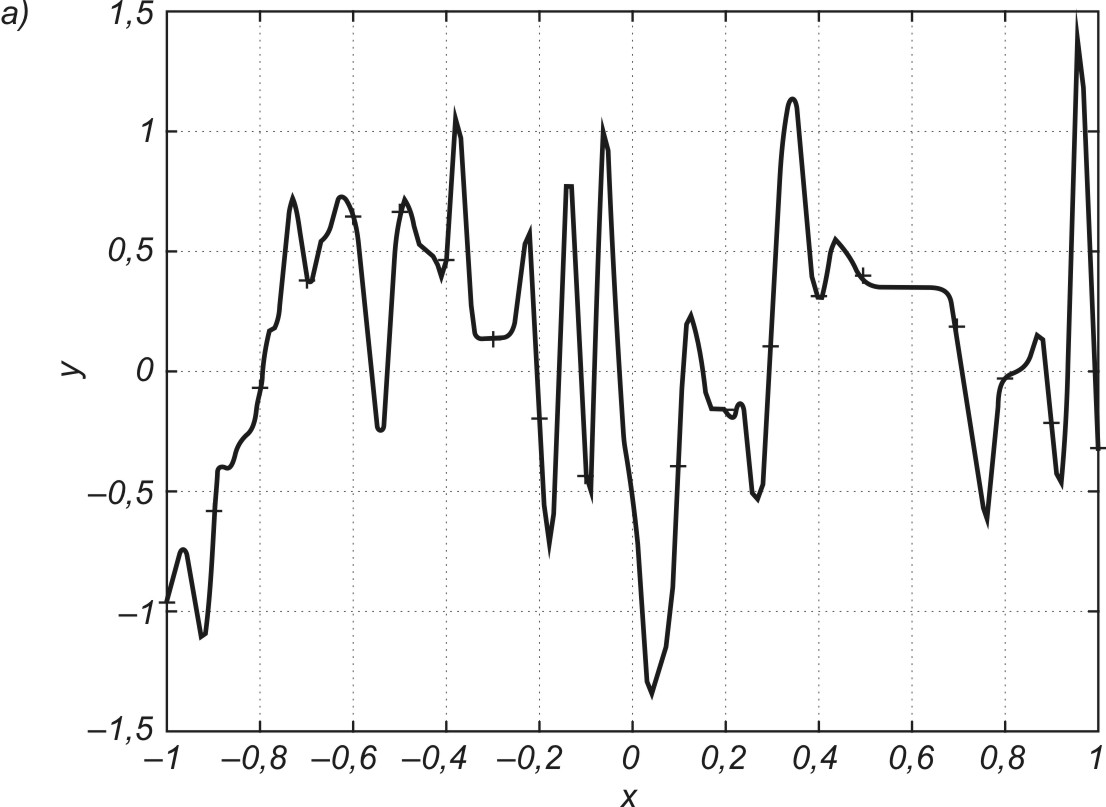
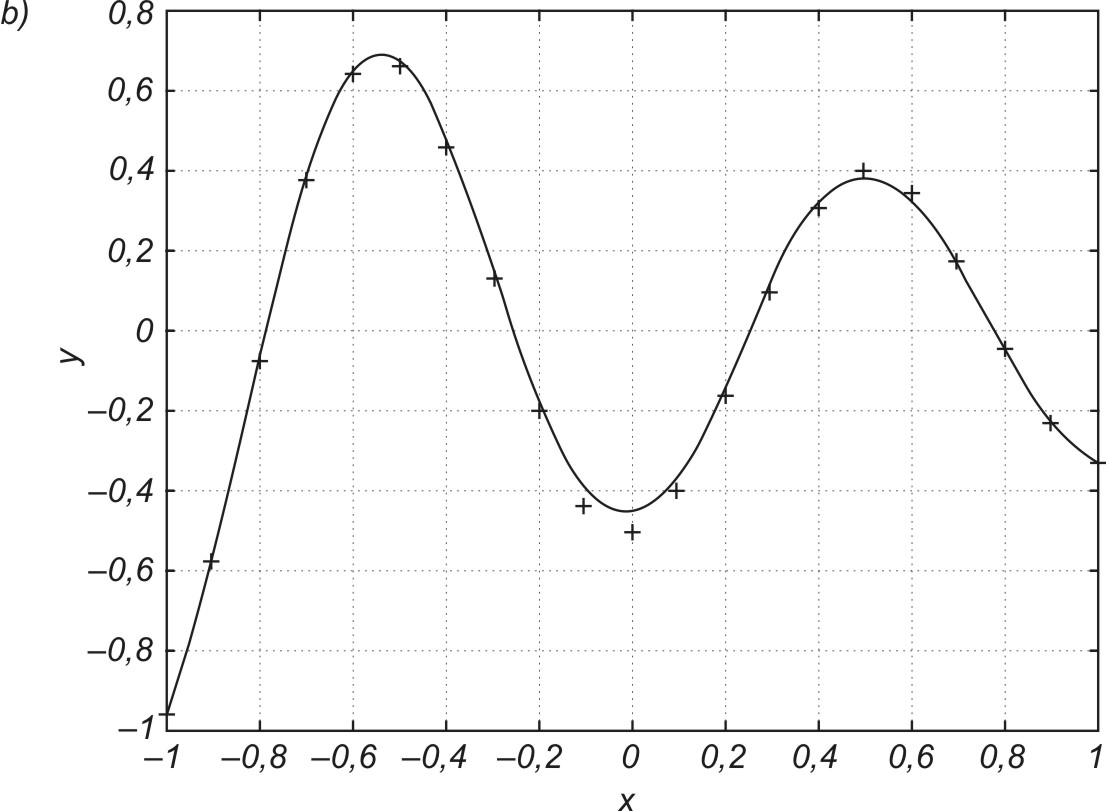
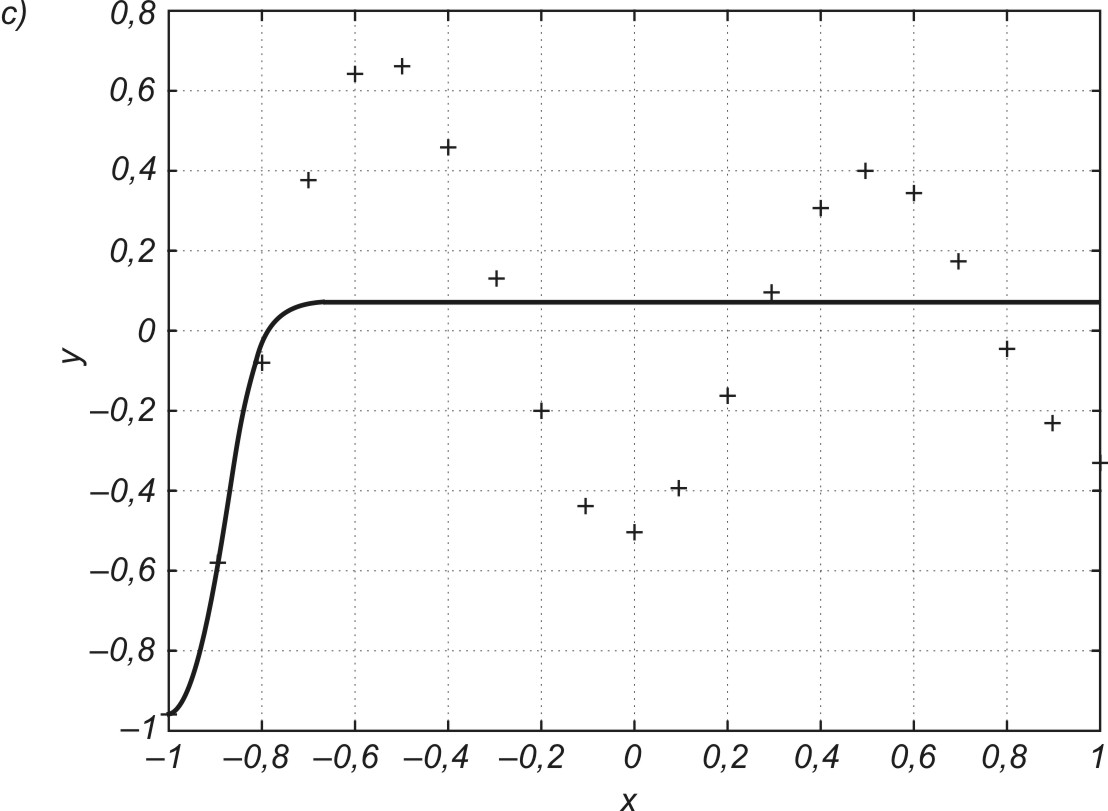
Na rys. 3.4a przedstawiono graficzną ilustrację efektu przewymiarowania sieci, często kojarzone z tak zwanym przeuczeniem sieci występującym przy zbyt dużej liczbie neuronów i połączeń wagowych. Sieć aproksymująca zawierająca 80 neuronów w warstwie ukrytej (241 wag) dopasowała swoje odpowiedzi do 21 zadanych punktów sinusoidy poddanej aproksymacji, na zasadzie interpolacji, dając zerowy błąd uczenia. Minimalizacja błędu uczenia na zbyt małej (w stosunku do liczby wag) liczbie danych uczących spowodowała dowolność wartości wielu połączeń wagowych, która przy zmianie punktów testujących względem uczących jest przyczyną znacznego odchylenia aktualnej wartości y od spodziewanej wartości d. Zmniejszenie liczby neuronów ukrytych do 5 (odpowiada temu 16 wag sieci), przy nie zmienionej liczbie próbek uczących, pozwoliło uzyskać zarówno mały błąd uczenia, jak i dobrą zdolność generalizacji (rys. 3.4b). Dalsze zmniejszanie liczby neuronów ukrytych może spowodować niezdolność sieci do akceptowalnej dokładności odwzorowania danych uczących (zbyt duży błąd uczenia). Przypadek taki zilustrowano na rys. 3.4c, gdzie użyto tylko jednego neuronu ukrytego (liczba połączeń wagowych równa 4). Sieć nie była zdolna dokonać poprawnego odwzorowania danych uczących, gdyż liczba stopni swobody (4 wagi) takiej sieci jest za mała w stosunku do wymagań odwzorowania 21 punktów zadanych. W takim przypadku nie można oczywiście uzyskać dobrych zdolności generalizacyjnych, gdyż zależą one w sposób oczywisty od poziomu błędu uczenia.

Istotnym problemem jest obiektywna ocena rozwiązania. Powszechnie stosowana metoda jest walidacja krzyżowa (ang. cross validation) służącej do oceny jakości działania sieci neuronowej. Technika ta polega na podziale dostępnego zbioru danych na M podzbiorów, z których (M-1) jest używanych do uczenia a pozostały podzbiór do testowania. Uczenie sieci przeprowadza się wielokrotnie stosując wszystkie możliwe kombinacje podzbiorów do tworzenia zbioru uczącego i pozostawiając zawsze jeden podzbiór do testowania. W ten sposób wszystkie dostępne dane uczestniczą w procesie walidacji (testowania na danych nie uczestniczących w uczeniu). Ocena jakości działania sieci wynika z uśrednionych (po wszystkich próbach) wyników testowania.

Szczególną postacią tej formy jest technika ,,leave one out" w której każdy podzbiór jest jednoelementowy. Przy p parach danych oznacza to uczenie sieci na (p-1) wzorcach i testowanie ograniczone do jednego wzorca. Uczenie przeprowadza się p razy zamieniając za każdym razem jedną próbkę testującą. Jakość rozwiązania ocenia się na podstawie uśrednionych wyników wszystkich prób. Jest to technika polecana w przypadku małej liczby dostępnych danych.

Powszechnie stosowaną metodą jest również wielokrotne powtórzenie uczenia/testowania na losowo dobranych zbiorach uczącym i testującym (typowy podział to 0.7 danych do uczenia i 0.3 danych do testowania. W każdej powtórce procesu inny jest zestaw testujący. Przy wielokrotnym powtórzeniu procesu (np. 100 razy) uzyskuje się wartość średnią odwzorowującą obiektywną informację o jakości działania sieci.