Podręcznik
3. Sieci neuronowe głębokie
3.8. Autoenkoder
6.8.1 Struktura autoenkodera
Autoenkoder jest specjalnym rozwiązaniem sztucznej sieci neuronowej, którego zadaniem jest skopiowanie danych wejściowych w wyjściowe z akceptowalnym błędem [18,33] za pośrednictwem warstw ukrytych o zredukowanym wymiarze względem wymiaru danych wejściowych. Jest to wielowarstwowy układ autoasocjacyjny stowarzyszający dane wejściowe ze sobą. Struktura składa się z dwu następujących po sobie części: układu kodującego (enkoder) rzutującego dane wejściowe w postaci wektora x w dane zakodowane reprezentowane przez wektor \( \mathbf{h}=\mathbf{f}(\mathbf{x}) \) i dekodera wykonującego działanie odwrotne rekonstruujące z określoną dokładnością dane wejściowe \( \mathbf{x}^{\prime}=\mathbf{g}(\mathbf{h}) \). Przykład struktury autoenkodera o jednej warstwie sygnałów zakodowanych i części dekodującej przedstawiony jest na rys. 6.23. Dane wejściowe w postaci wektora \( \mathbf{x} \) są kodowane w wektorze \( \mathbf{h} \) jako sygnały ukryte (część tworząca enkoder). Dekodowanie odbywa się w strukturze symetrycznej, odtwarzając za pośrednictwem wektora \( \mathbf{h} \) wektor \( \mathbf{x^{\prime}} \) (część zwana dekoderem).
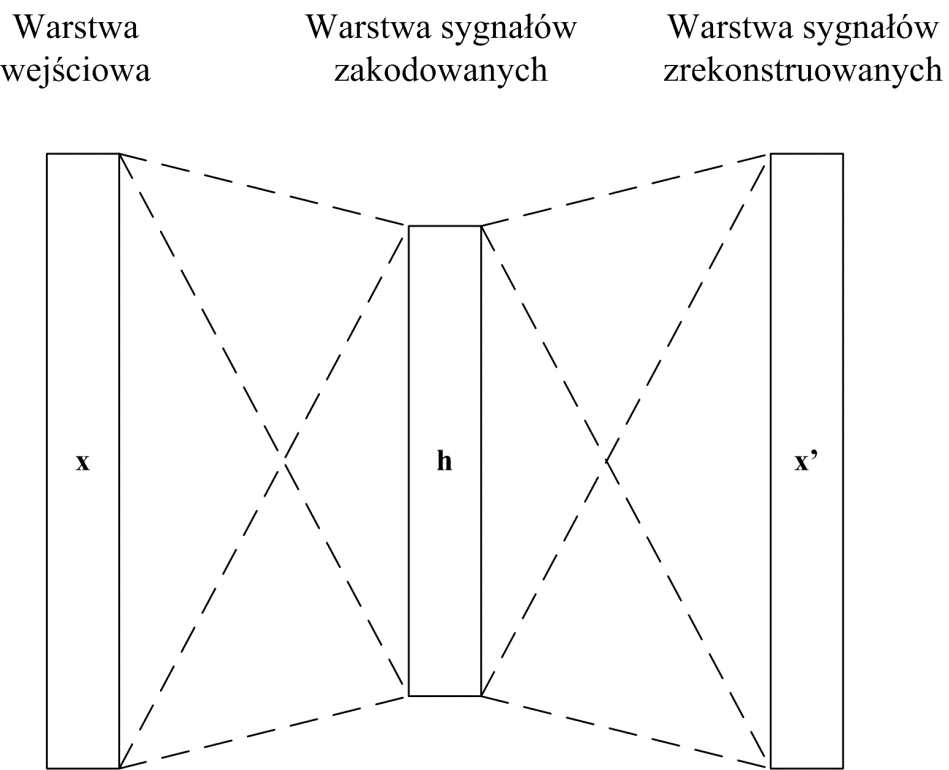
Podstawą działania jest kompresja danych polegająca na wychwyceniu głównych cech procesu reprezentowanego przez zbiór wektorów x. Oznacza to, że dane zrekonstruowane \( \mathbf{x^{\prime}} \) nie reprezentują dokładnych kopii danych wejściowych ale ich aproksymację. Wektor \( \mathbf{h} \) stanowiący podstawę kodowania i następnie rekonstrukcji, reprezentuje zatem cechy główne procesu eliminując elementy nieistotne (traktowane jako szum) zawarte w zbiorze danych wejściowych \( \mathbf{x} \). Autoenkoder jest uogólnieniem dwuwarstwowej sieci liniowej PCA. Różni go od niej liczba warstw, która może być dowolna, jak również nieliniowa funkcja aktywacji neuronów stosowana w przypadku ogólnym.
Bezpośrednie, dokładne kopiowanie danych uczących \( \mathbf{x} \) w siebie nie ma sensu praktycznego, gdyż nie pozwala na wychwycenie najważniejszych cech procesu zawartych w zbiorze danych uczących. Dopiero ograniczenie liczby neuronów warstwy ukrytej definiującej kodowanie danych wejściowych zmusza proces uczenia do wychwycenia cech najważniejszych, i pominięcie cech drugorzędnych, nie mających większego wpływu na wynik rekonstrukcji danych. Proces uczenia sieci może być zdefiniowany jako dobór parametrów (wag neuronowych) prowadzący do minimalizacji funkcji kosztu (celu) \( E(\mathbf{x}, \mathbf{g}(\mathbf{h}(\mathbf{x})) \) .
Podstawowa definicja funkcji kosztu przyjmowana jest zwykle w postaci wartości błędu średniokwadratowego po wszystkich zmiennych \(n= 1, 2,\ldots, N \) dla danych uczących przy \(k=1, 2, \ldots, p\), przy czym \(N\) jest wymiarem wektora wejściowego a \(p\) liczbą danych uczących (obserwacji).
| \( E=\frac{1}{p} \sum_{n=1}^N \sum_{k=1}^p\left(x_n^{(k)}-x_n^{\prime(k)}\right)^2=\frac{1}{p} \sum_{n=1}^N \sum_{k=1}^p\left(x_n(k)-g_n\left(\mathbf{h}\left(\mathbf{x}(k)\right)\right)^2\right. \) | (6.21) |
Dla uzyskania lepszej odporności autoenkodera na szum w uczeniu stosuje się również wersję zmodyfikowaną, w której zamiast dopasowywać sygnały wyjściowe \( \mathbf{g}(\mathbf{h}(\mathbf{x})) \) do sygnałów wejściowych \( \mathbf{x} \), porównanie z sygnałami \( \mathbf{x} \) dotyczy odpowiedzi autoenkodera \( \mathbf{g}(\mathbf{h}(\mathbf{x}_s)) \) na sygnały zaszumione \( \mathbf{x}_s \). Układ przetwarza wówczas \( \mathbf{x}_s \) w taki sposób aby uzyskać na wyjściu najlepszą możliwie aproksymację wektorów oryginalnych \( \mathbf{x} \). Oznacza to, że funkcja celu podlegająca minimalizacji przyjmuje zmodyfikowaną formę
| \( E=\frac{1}{p} \sum_{n=1}^N \sum_{k=1}^p\left(x_n(k)-g_n\left(\mathbf{h}\left(\mathbf{x}_s(k)\right)\right)^2\right. \) | (6.22) |
Zastosowanie liniowej funkcji aktywacji neuronów przy jednej warstwie ukrytej prowadzi do znanego rozwiązania PCA. Autoenkoder stosujący nieliniowe funkcje aktywacji i kilka warstw ma wiele zalet w stosunku do rozwiązania liniowego, z których najważniejsze to [18]
-
duża oszczędność (ang. sparsity) w reprezentacji danych,
-
ograniczone wartości pochodnej sygnałów,
-
krzepkość systemu względem szumu oraz brakujących danych.
Oszczędność autoenkodera może być osiągnięta w procesie uczenia poprzez włączenie do funkcji kosztu czynnika kary za nadmiernie rozbudowaną strukturę. Wówczas zmodyfikowana funkcja kosztu \( E \) przyjmie postać
| \( E=E\left(\mathbf{x}, \mathbf{g}(\mathbf{h}(\mathbf{x}))+\lambda \Omega_1(\mathbf{h})\right. \) | (6.23) |
w której wielkość \( E(\mathbf{x}, \mathbf{g}(\mathbf{h}(\mathbf{x}))) \) reprezentuje klasyczną definicję funkcji kosztów, a \( \lambda \) stanowi współczynnik regularyzacji. Funkcja \( \Omega_1(\mathbf{h}) \) stanowi karę za zbyt rozbudowaną strukturę układu. Typowa definicja tej funkcji to
| \( \Omega_1(\mathbf{h})=\frac{1}{2} \sum_h \sum_{i, j}\left(w_{i j}^{(h)}\right)^2 \) | (6.24) |
gdzie \( h \) reprezentuje warstwy ukryte zastosowane w rozwiązaniu. W wyniku uczenia wymusza się zmniejszenie wartości wag określonych grup neuronów. W efekcie pewne połączenia synaptyczne o małej wartości wag mają minimalny wpływ na działanie systemu.
Dla dalszego zmniejszenia wpływu zmian danych wejściowych \( \mathbf{x} \) na wynik działania układu wprowadza się regularyzację uwzględniającą pochodne sygnałów warstwy ukrytej względem elementów wektora wejściowego \( \mathbf{x} \). Funkcja regularyzacyjna przyjmuje wówczas następującą formę [18]
| \( \Omega_2(\mathbf{h}, \mathbf{x})=\sum_{h=1}^H\left\|\nabla_x h_i\right\|^2 \) | (6.25) |
w której \( \nabla_x h_i \) oznacza wektor pochodnych sygnałów \( h_i \) warstw ukrytych względem składowych wektora wejściowego \( \mathbf{x} \). Taki rodzaj regularyzacji zmusza algorytm uczący do wytworzenia sygnałów wyjściowych sieci, które zmieniają się niewiele przy niewielkich zmianach wartości sygnałów wejściowych.
Inny rodzaj regularyzacji autoenkodera uwzględnia zgodność średniej statystycznej aktywacji neuronów \( \hat{\rho_i} \) w aktualnym stanie uczenia z jej wartością pożądaną \( \rho_i \). Wartość aktualna jest określona dla pojedynczego neuronu warstwy ukrytej w postaci
| \( \hat{\rho}_i=\frac{1}{p} \sum_{j=1}^p h_i\left(\boldsymbol{x}_j\right) \) | (6.26) |
gdzie \( p \) oznacza liczbę obserwacji (wektorów \( \mathbf{x} \)). Mała wartość średniej aktywacji neuronu oznacza, że neuron ten aktywuje się jedynie dla niewielkiej ilości danych wejściowych, specjalizując się w ich reprezentacji. Dodając taki czynnik do minimalizowanej funkcji kosztu zmusza się neurony do reprezentowania jedynie określonych (specyficznych) cech procesu.
W praktyce czynnik regularyzacyjny definiuje się z wykorzystaniem dywergencji Kullbacka-Leiblera, mierzącego zgodność wartości aktualnej z pożądaną wartością średniej funkcji aktywacji dla określonego zbioru danych. Składnik regularyzacyjny definiuje się w postaci [18]
| \( \Omega_3(\rho)=\sum_i \rho_i \log \left(\frac{\rho_i}{\hat{\rho}_i}\right)+\left(1-\rho_i\right) \log \left(\frac{1-\rho_i}{1-\hat{\rho}_i}\right) \) | (6.27) |
Regularyzacja Kulbacka-Leiblera jest statystyczną miarą zgodności dwu rozkładów stochastycznych. Przyjmuje małą wartość, przy niewielkiej niezgodności i wartość zerową gdy \( \hat{\rho_i} =\rho \). Przy wzrastającej niezgodności miara ta rośnie.
W praktyce definiuje się wartość pożądaną stosunku \( \rho_i /\hat{\rho_i} \) (w Matlabie [38] jest to parametr zwany 'SparsityProportion' przyjmujący wartość dodatnią z przedziału [(0, 1) z wartością wbudowaną 0.05). Dzięki zastosowaniu tego typu regularyzacji poszczególne neurony ukryte „specjalizują” się w wytwarzaniu dużego sygnału jedynie dla małej liczby danych uczących (lokalizacja aktywności) co oznacza w ogólności lepsze, bo wyspecjalizowane działanie sieci.
W efekcie, w procesie uczenia minimalizacji podlega funkcja kosztu zmodyfikowana o poszczególne rodzaje czynników regularyzacyjnych. W ogólności zadanie minimalizacji może przyjąć następującą postać [18,43]
| \( \min E=\frac{1}{p} \sum_{n=1}^N \sum_{k=1}^p\left(\mathbf{x}_n(k)-g_n\left(\mathbf{h}\left(\tilde{\mathbf{x}}(k)\right)\right)^2+\lambda_1 \Omega_1(\mathbf{h})+\lambda_2 \Omega_2(\mathbf{h}, \mathbf{x})+\lambda_3 \Omega_3(\rho)\right. \) | (6.28) |
w której współczynniki \( \lambda_i \) (dobierane przez użytkownika) stanowią wagi, z jakimi poszczególne funkcje regularyzacyjne wpływają na wartość funkcji kosztu. Taka postać wymusza kompromis między zgodnością zrekonstruowanego sygnału wyjściowego układu z wartościami wejściowymi a złożonością tego układu, uwzględniając jednocześnie wrażliwość na niewielkie zmiany mogące nastąpić w rozkładzie wartości sygnałów wejściowym w trybie odtwarzania.
Istnieją różne implementacje algorytmu uczącego. Najbardziej popularne podejście polega na stopniowym uczeniu następujących po sobie warstwach. Proces rozpoczyna się w warstwie pierwszej, dla której sygnałami wejściowymi są sygnały oryginalne opisane wektorem \( \mathbf{x} \)), a sygnały wyjściowe oznaczone są jako \( \hat{\mathbf{x}} \)). Celem uczenia jest dobór liczby neuronów ukrytych i wag tych neuronów, które zapewnią właściwe (zgodnie z regularyzowaną funkcją celu) odtworzenie sygnałów wejściowych w warstwie wyjściowej (rys. 6.24a). W tej sytuacji sygnały warstwy ukrytej stanowią kod sygnałów wejściowych dla następnej warstwy, a warstwa wyjściowa podlega eliminacji.
| a) | 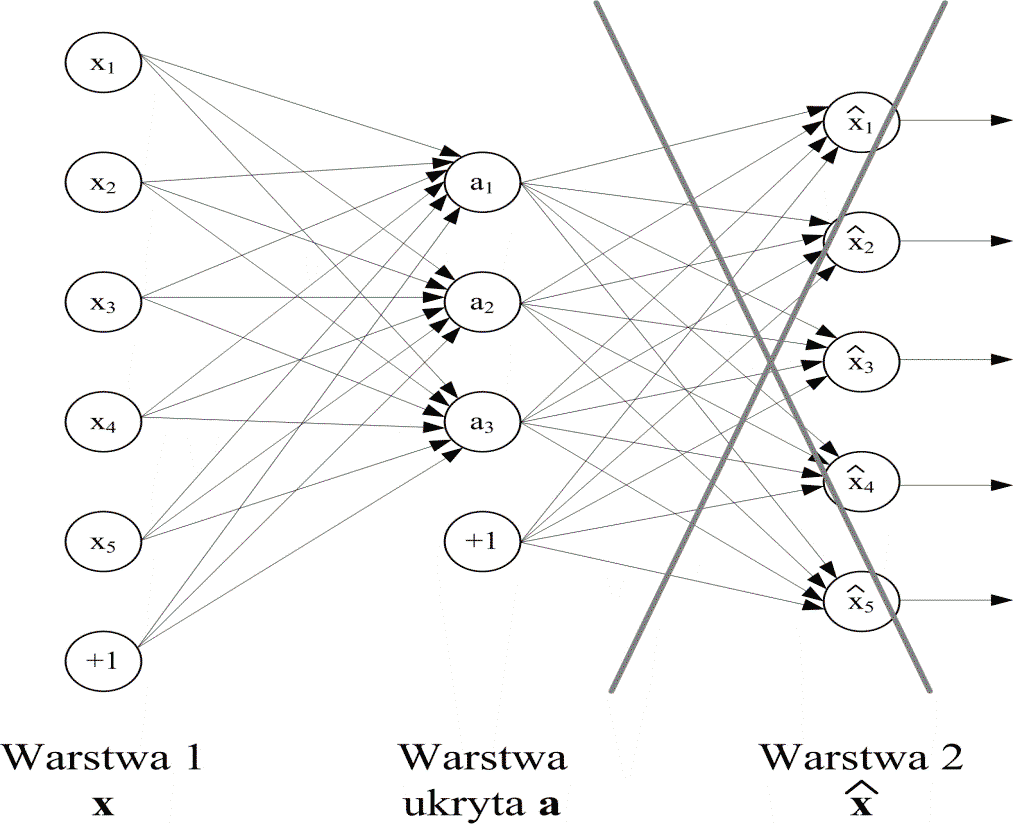 |
|---|---|
| b) | 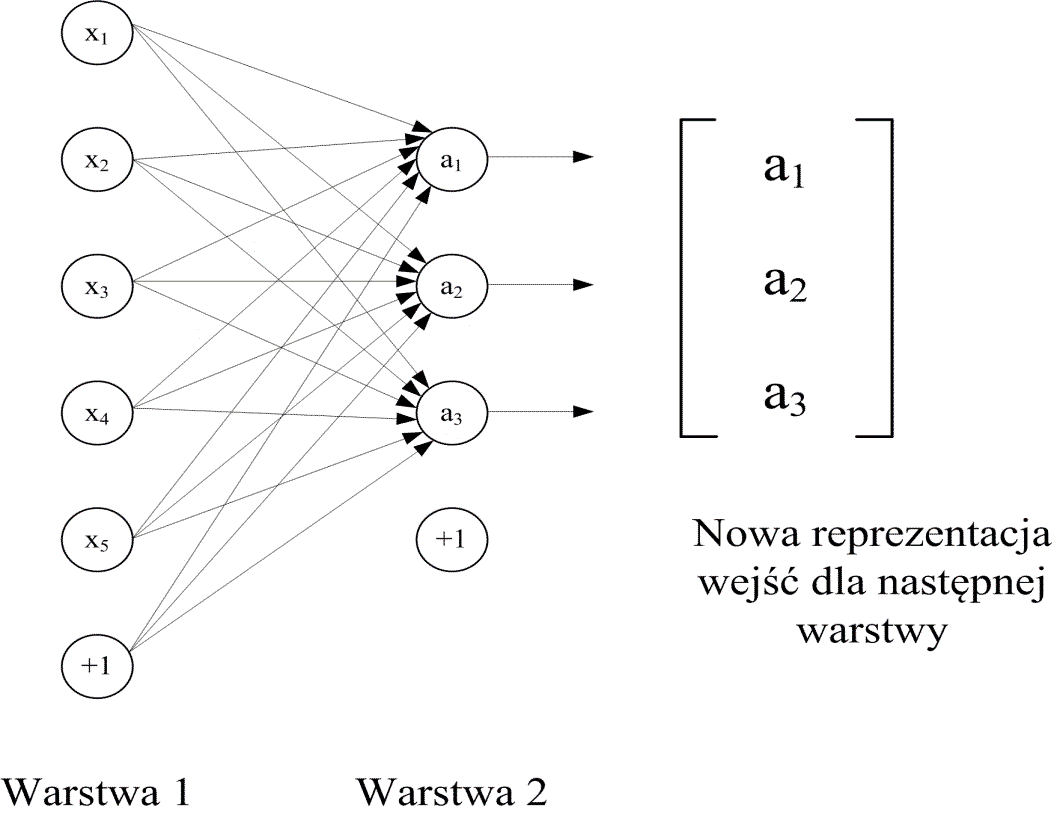 |
Po doborze parametrów warstwy ukrytej odrzuca się warstwę rekonstrukcji i sygnały z warstwy ukrytej stają się wejściowymi dla następnej warstwy (rys. 6.24b). Proces uczenia jest kontynuowany dla następnej warstwy, dobierając jej parametry w taki sposób, aby uzyskać możliwie najlepsze odwzorowanie sygnałów wejściowych \( \mathbf{a} \) w sygnały wyjściowe. W efekcie po odrzuceniu warstwy wyjściowej sieć zawiera dwie warstwy neuronowe \( \mathbf{a} \) i \( \mathbf{b} \) jak to pokazano na rys. 6.25, przy czym liczba neuronów w każdej kolejnej warstwie jest kolejno redukowana, zmuszając sieć do kompresji danych.
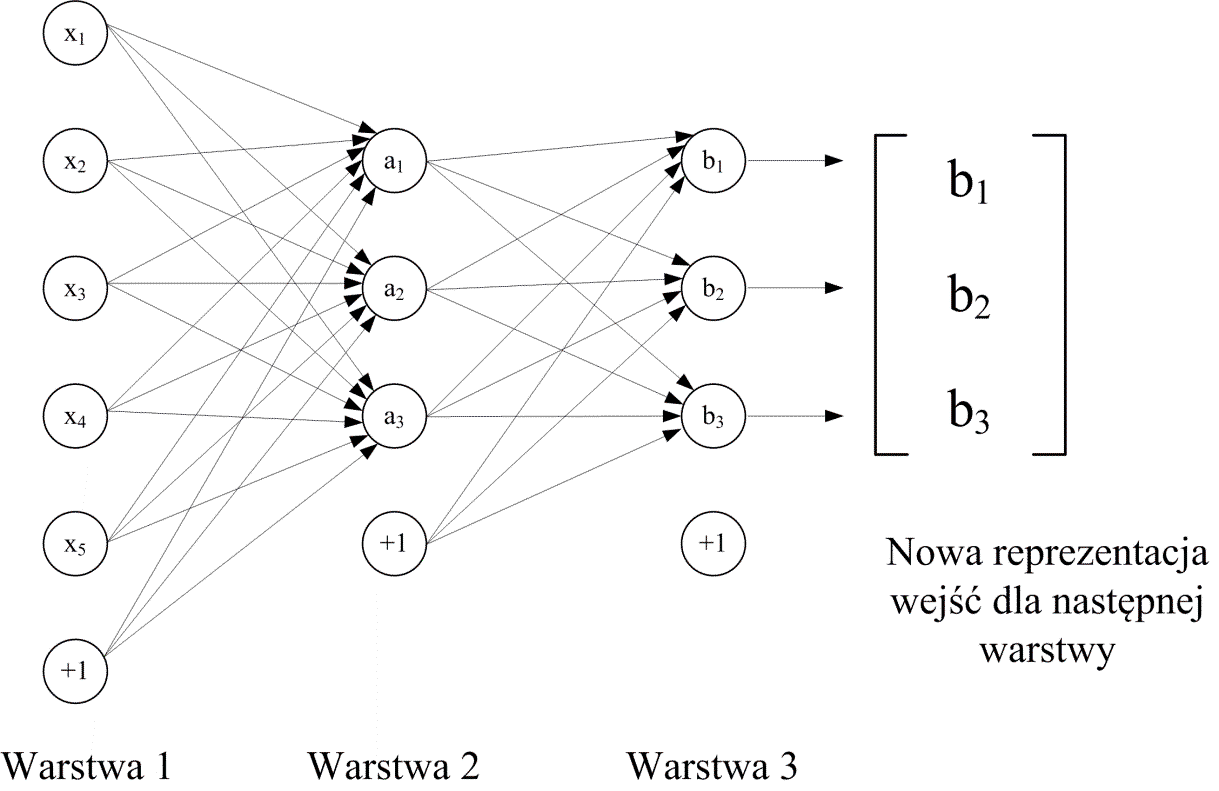
Sygnały warstwy ukrytej \( \mathbf{b} \) stają się ponownie sygnałami wejściowymi dla ukształtowania następnej warstwy o dalej zredukowanej liczbie neuronów Proces jest następnie kontynuowany dla następnych warstw, w sposób identyczny do omówionego. Kształtowanie kolejnych warstw autoenkodera może odbywać się przy użyciu dowolnego algorytmu gradientowego. Jest to stosunkowo prosty proces ze względu na fakt, że w każdym etapie uczenie dotyczy tylko parametrów jednej warstwy.
Ostatnia warstwa ukryta autoenkodera (po wyeliminowaniu warstwy rekonstrukcyjnej) zawiera kodowanie na najwyższym poziomie, zwykle o najbardziej ograniczonej liczbie neuronów. Sygnały wyjściowe tej warstwy stanowią cechy diagnostyczne wyselekcjonowane przez strukturę układu w procesie uczenia z udziałem zbioru danych uczących. Mogą one stanowić atrybuty wejściowe dla końcowego stopnia klasyfikatora bądź układu regresyjnego o dowolnej konstrukcji.
6.8.4 Przykład zastosowania autoenkodera w kodowaniu danych
Poniżej przedstawiony będzie przykład zdolności kodowania autoenkodera dla zbioru 8 obrazów czarno-białych o wymiarach 64x64 reprezentowanych na rys. 6.26 i zawartych w plikach RBx.png. Zbiór ten został użyty najpierw w uczeniu a następnie przetestowane zostało odtwarzanie zakodowanych obrazów (identycznych jak w uczeniu). Zastosowano jedną warstwę ukrytą o 30 neuronach. Współczynnik kompresji równał się więc 4096/30=136.6.

Linie programu Matlaba podane są jak niżej
x1=imread('RB1.png');x2=imread('RB2.png');x3=imread('RB3.png');x4=imread('RB4.png');
x5=imread('RB9.png');x6=imread('RB6.png');x7=imread('RB7.png');x8=imread('RB8.png');
xc{1,1}=x1; xc{1,2}=x2;xc{1,3}=x3; xc{1,4}=x4;
xc{1,5}=x5; xc{1,6}=x6;xc{1,7}=x7; xc{1,8}=x8;
figure(1);
for i = 1:8
subplot(2,4,i);
imshow(xc{i}); title('Original')
end
hiddenSize = 20;
% 'ScaleData',false, ...
autoenc = trainAutoencoder(xc, hiddenSize, ...
'L2WeightRegularization', 0.004, ...
'SparsityRegularization', 4, ...
'SparsityProportion', 0.15, ...
'MaxEpochs', 1000);
xReconstructed = predict(autoenc, xc);
figure(2);
for i = 1:8
subplot(2,4,i);
% imshow((xReconstructed{i})>0.5); title('Reconstructed')
imshow(xReconstructed{i}); title('Reconstructed')
end
figure(3)
for i = 1:8
err=xReconstructed{i}-double(xc{i});
errBW(err<0.5)=0;
errBW(err>=0.5)=1;
nerr(i)=sum(errBW);
subplot(2,4,i);
% imshow(1-err);
imshow(reshape(1-errBW,64,64)); title('Error')
end
liczba_err=nerr
rate_err=nerr/4096*100
Wygląd obrazów w skali szarości odtworzonych po rekonstrukcji przedstawiony jest na rys. 6.27. Szare piksele obrazu (ledwie widoczne) nałożone na inne czarno–białe obrazy odtworzone przez sieć mają niewielkie wartości, które przetworzone na reprezentację czarno-białą nie wnoszą istotnych błędów rekonstrukcji obrazów czarno-białych z rys. 6.27. Błąd rekonstrukcji kolejnych obrazów czarno-białych w postaci liczby błędnych pikseli (po wcześniejszym zaokrągleniu wartości pikseli do 1 lub 0) uzyskany w programie podany jest poniżej
Liczba błędnych pikseli kolejnych obrazów=[ 3 4 7 9 0 8 92 2]
Błąd odtworzenia dotyczył znikomej ilości pikseli w obrazach czarno-białych (oryginalna liczba pikseli każdego obrazu równa 4096). Jeden obraz czarno-biały został odtworzony bezbłędnie (wynik po zaokrągleniu do wartości bitów 1 lub 0). Procentowa zawartość błędów odtworzenia kolejnych obrazów czarno-białych jest równa
Błąd procentowy=[ 0.07% 0.10% 0.17% 0.22% 0 0.19% 2.25% 0.05%]
Należy zauważyć, że jest to wynik rekonstrukcji autoenkodera jedynie w trybie odtwarzania na tych samych danych, które były użyte w uczeniu. Świadczą one o dobrych wynikach uczenia sieci. Na tej podstawie nie można wyciągać daleko idących wniosków co do zdolności generalizacji systemu przy tej wartości współczynnika kompresji.

Sieć autoenkodera znajduje zastosowanie w typowych obszarach przetwarzania danych:
-
Redukcja szumu zakłócającego dane – w tym przypadku zakłada się, że dane wejściowe zniekształcone są szumem; po zakodowaniu i rekonstrukcji szum ten może ulec znacznej redukcji przy właściwym doborze parametrów sieci.
-
Generacja cech diagnostycznych procesu reprezentowanego przez dane uczące. W tym przypadku wyjściem sieci jest warstwa ukryta. W przypadku programu autoencoder Matlaba [43] dostęp do sygnałów h warstwy ukrytej (kodującej) odbywa się komendą
h=encode(autoenc, dane_wej)
gdzie autoenc jest nazwą struktury sieciowej użytej w wywołaniu autoenkodera, a dane_wej jest zbiorem danych które mają podlegać kodowaniu.
Program Matlaba zakłada istnienie jednej warstwy ukrytej. Przy strukturze wielowarstwowej jego wywołanie musi być wielokrotne, przy czym za każdym razem wymuszeniem dla następnej warstwy są sygnały wyjściowe warstwy ukrytej. Ostatnia warstwa ukryta reprezentować będzie najbardziej skompresowane cechy diagnostyczne procesu.
6.8.5 Przykład zastosowania autoenkodera w rozpoznaniu komórek krwiotwórczych
Przykład zastosowania autoenkodera przedstawiony zostanie przy rozpoznaniu 2 rodzajów komórek krwiotwórczych (kodowanie binarne zero-jedynkowe wektora destination \( \mathbf{T} \)) na podstawie 87 cech diagnostycznych typu numerycznego zawartych w macierzy \( \mathbf{X} \). Stosowane są 2 warstwy kodujące (ukryte) i warstwa typu Softmax na wyjściu, działająca w trybie klasyfikacji. Wydruk programu w Matlabie wykonującego zadanie przedstawiony jest poniżej. Dane dotyczące cech diagnostycznych (macierz sygnałów wejściowych \( \mathbf{X} \)) oraz przynależności klasowej kolejnych obserwacji (wektor \( \mathbf{T} \)) zawarte są w pliku Matlaba XT_autoencoder.mat.
load XT_autoencoder.mat
a=randperm(293);Xrand=X(:,a);Trand=T(:,a);
Xucz=Xrand(:,1:193);Tucz=Trand(:,1:193);
Xtest=Xrand(:,194:end); Ttest=Trand(:,194:end);
% Train an autoencoder with a hidden layer of assumed size and a linear transfer function for the% decoder. Set the L2 weight regularizer to 0.001, sparsity regularizer to 4 and sparsity
% proportion to 0.05.
hiddenSize = 60;
autoenc1 = trainAutoencoder(Xucz,hiddenSize,...
'L2WeightRegularization',0.001,...
'SparsityRegularization',4,...
'SparsityProportion',0.05,...
'DecoderTransferFunction','purelin');
% Extract the features in the hidden layer.
features1 = encode(autoenc1,Xucz);
% Train a second autoencoder using the features from the first autoencoder. Do not scale
% the data.
hiddenSize = 29;
autoenc2 = trainAutoencoder(features1,hiddenSize,...
'L2WeightRegularization',0.001,...
'SparsityRegularization',4,...
'SparsityProportion',0.05,...
'DecoderTransferFunction','purelin',...
'ScaleData',false);
% Extract the features in the hidden layer.
features2 = encode(autoenc2,features1);
% Train a softmax layer for classification using the features, features2, from the second
% autoencoder, autoenc2.
softnet = trainSoftmaxLayer(features2,Tucz,'LossFunction','crossentropy');
% Stack the encoders and the softmax layer to form a deep network.
deepnet = stack(autoenc1,autoenc2,softnet);
% Train the deep network on the data.
% Construct Deep Network Using Autoencoders % 2-3
deepnet = train(deepnet,Xucz,Tucz);
% Estimate the cell types using the trained deep network: deepnet.
cell_type = deepnet(Xtest);
% Plot the confusion matrix.
plotconfusion(Ttest,cell_type);
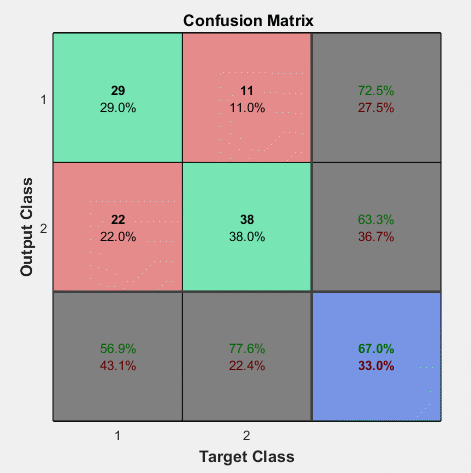
Wynik testowania sieci na danych testujących nie uczestniczących w uczeniu jest zależny od losowego podziału zbioru danych na zbiór uczący i testujący i może przyjmować różne wartości w zależności od ich składu. Przykładowy wynik dla jednej próby w postaci macierzy rozkładu klas (ang. confusion matrix) przedstawiony jest na rys. 6.28.