Podręcznik

2. Sieci wektorów nośnych SVM

2.3. Sieć nieliniowa SVM w zadaniu klasyfikacji

Nieseparowalność liniowa wzorców nie oznacza braku ich separowalności w ogóle. Powszechnym rozwiązaniem, zastosowanym między innymi w poznanych już sieciach RBF jest nieliniowe zrzutowanie danych oryginalnych w inną przestrzeń funkcyjną, w której wzorce te są liniowo separowalne, bądź prawdopodobieństwo ich separowalności jest bliskie jedności. Podstawę matematyczną stanowi tu twierdzenia Covera [59,68], zgodnie z którym wzorce nieseparowalne liniowo w przestrzeni oryginalnej mogą być przetransformowane w inną przestrzeń parametrów, tak zwaną przestrzeń cech, zwykle o wymiarze $K \ge N$ , w której z dużym prawdopodobieństwem stają się separowalne liniowo. Warunkiem jest zastosowanie transformacji nieliniowej o odpowiednio wysokim wymiarze $K$ przestrzeni cech.

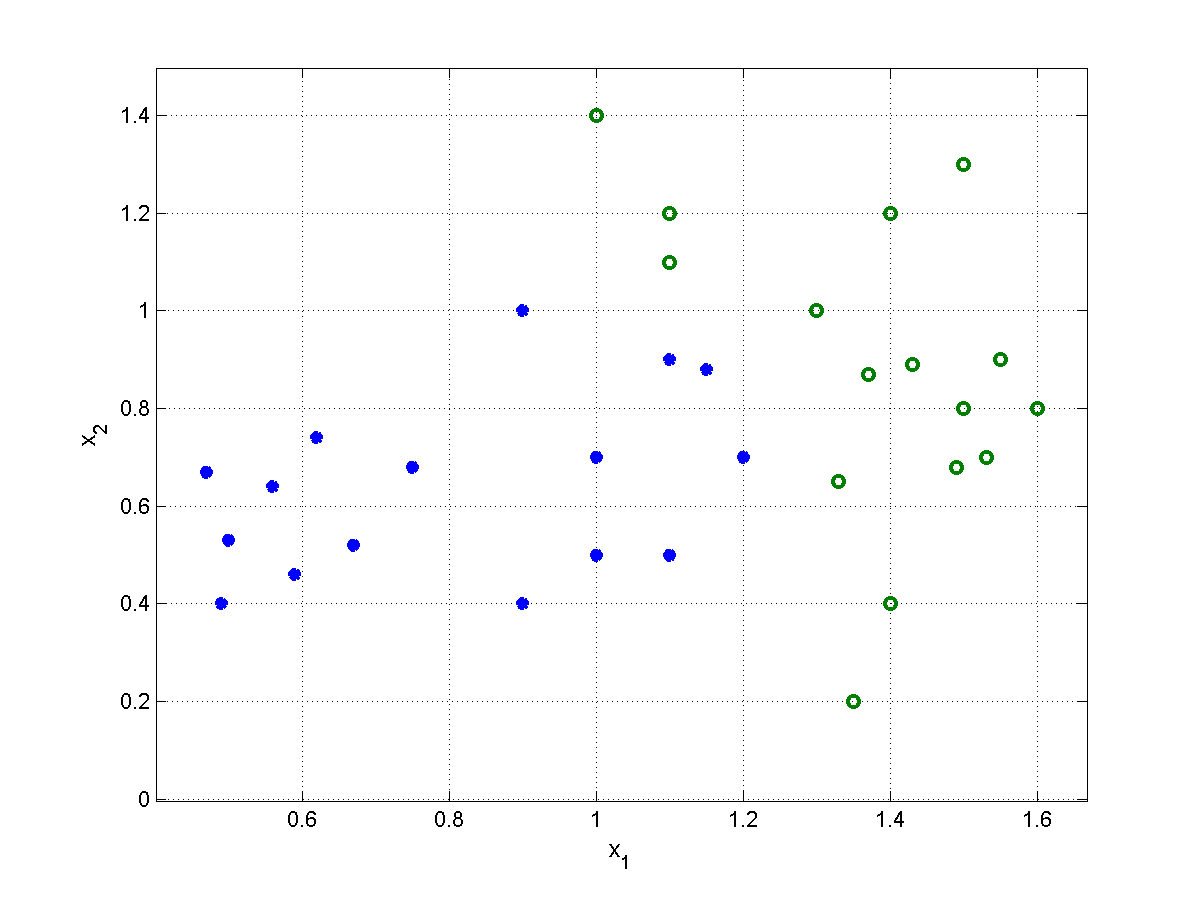
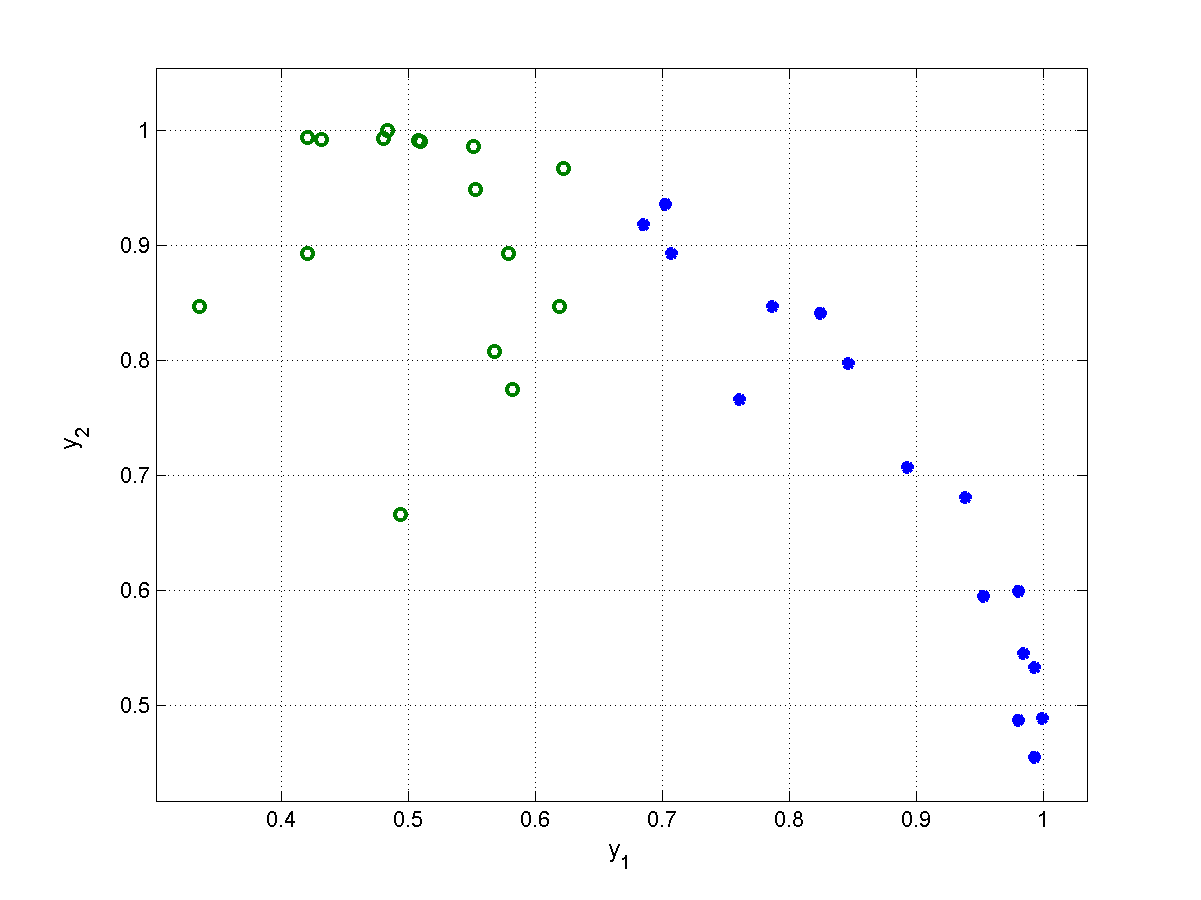
Rys. 5.3 Ilustracja nieliniowej transformacji wzorców nieseparowalnych liniowo w zbiór liniowo separowalny

Rys. 5.3 przedstawia szczególny przykład nieliniowej transformacji wzorców należących do dwu klas nieseparowalnych liniowo (klasa $1$ oznaczona gwiazdką i klasa $2$ oznaczona symbolem o, obie określone w przestrzeni dwuwymiarowej, $N=2$ ), w przestrzeń funkcyjną zdefiniowaną za pośrednictwem 2 funkcji gaussowskich przy równej dla obu funkcji wartości $\sigma^2=1,5$ oraz wartościach centrów $\mathbf{c}_1=[0,5 ;\ 0,5]^T$ , $\mathbf{c}_2=[1,5 ;\ 0,8]^T$ . Wzorce oryginalne nieseparowalne w przestrzeni dwuwymiarowej (rys. 5.3a) po transformacji nieliniowej stają się separowalne (rys. 5.3b) i mogą być rozdzielone jedną hiperpłaszczyzną separującą. Zauważmy, że w tym szczególnym przykładzie wystarczyło użycie tylko dwu funkcji nieliniowych, aby przekształcić problem nieseparowalny liniowo w problem całkowicie separowalny.

W ogólności, jeśli $\mathbf{x}$ oznacza wektor wejściowy opisujący wzorzec, to po zrzutowaniu go w przestrzeń $K$ -wymiarową jest on reprezentowany przez zbiór $K$ cech $\varphi_j(\mathbf{x})$ dla $j= 1, 2, \ldots, K$ tworzący wektor $\boldsymbol{\varphi}(x)=[ \varphi_1(\mathbf{x}), \varphi_2(\mathbf{x}), \ldots, \varphi_K(\mathbf{x})]^T$ . W efekcie takiej transformacji równanie hiperpłaszczyzny w przestrzeni liniowej określone wzorem $y(\mathbf{x})=\mathbf{w}^T \boldsymbol{\varphi(\mathbf{x})}+b=0$ może być zastąpione przez równanie hiperpłaszczyzny w przestrzeni cech, które można zapisać w postaci

$y(\mathbf{x})=\mathbf{w}^T \boldsymbol{\varphi}(\mathbf{x})+b=\sum_{j=1}^K w_j \varphi_j(\mathbf{x})+b=0$

(5.21)

w której $w_j$ oznaczają wagi prowadzące od $\varphi_j(\mathbf{x})$ do neuronu wyjściowego, $\mathbf{w} = [w_1, w_2, \ldots, w_K]^T$ . Wektor wag $\mathbf{w}$ jest $K$ -wymiarowy a $b$ oznacza wagę polaryzacji. Cechy procesu opisane funkcjami $\varphi_j(\mathbf{x})$ przejęły rolę poszczególnych zmiennych $x_j$ . Wartość sygnału wyjściowego sieci opisuje teraz równanie

$y(\mathbf{x})=\mathbf{w}^T \boldsymbol{\varphi}(\mathbf{x})+b=0$

(5.22)

Równaniu (5.22) można przyporządkować strukturę sieci neuronowej analogiczną do sieci RBF, omówioną w rozdziale poprzednim jak to przedstawiono na rys. 5.4.

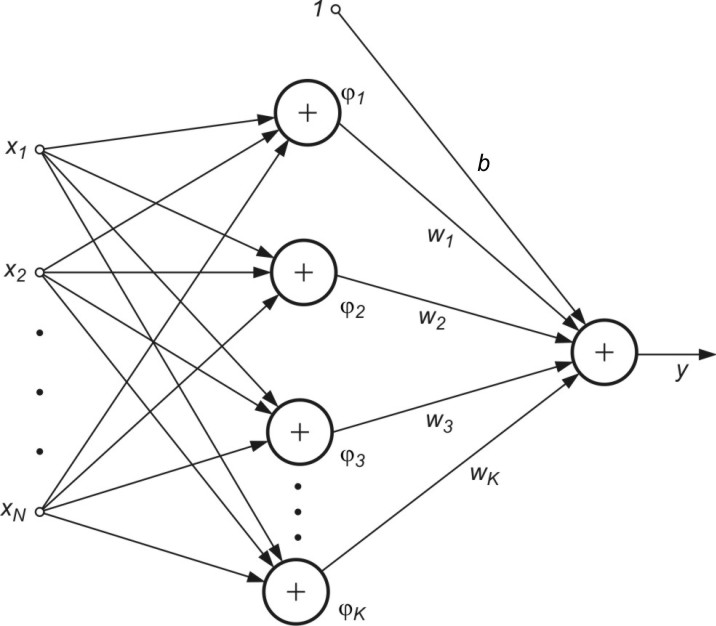
Rys. 5.4 Struktura wyjściowa nieliniowej sieci SVM

Zasadniczą różnicę w stosunku do sieci RBF stanowi fakt, że funkcje $\varphi_j(\mathbf{x})$ mogą przyjmować dowolną postać, w szczególności radialną, sigmoidalną czy wielomianową. Traktując warstwę ukrytą sieci jedynie jako układ rzutujący dane oryginalne w przestrzeń cech, w której są one liniowo separowalne, można traktować sygnały $\varphi_j(\mathbf{x})$ jako wymuszenia dla sieci liniowej SVM. Wszystkie zależności wyprowadzone dla sieci liniowej obowiązują zatem również tutaj, przy formalnym zastąpieniu wektora $\mathbf{x}$ przez wektor $\boldsymbol{\varphi}(\mathbf{x})$ . W szczególności problem pierwotny uczenia można przepisać w postaci

$\min \limits_{\mathbf{w}} \frac{1}{2} \mathbf{w}^T \mathbf{w}+C \sum_{i=1}^p \xi_i$

(5.23)

przy ograniczeniach liniowych ( $i=1, 2, …, p)$

$\begin{aligned} d_i\left(\mathbf{w}^T \boldsymbol{\varphi}\left(\mathbf{x}_i\right)+b\right) &\geq 1-\xi_i \\ \xi_i &\geq 0 \end{aligned}$

(5.24)

Rozwiązanie problemu pierwotnego odbywa się poprzez jego transformację do problemu dualnego, identycznie jak dla sieci o liniowej separowalności wzorców poprzez minimalizację funkcji Lagrange'a [59,68]

$J(\mathbf{w}, b, \boldsymbol{\alpha}, \boldsymbol{\xi}, \boldsymbol{\mu})=\frac{1}{2} \mathbf{w}^T \mathbf{w}+C \sum_{i=1}^p \xi_i-\sum_{i=1}^p \alpha_i\left[d_i\left(\mathbf{w}^T \boldsymbol{\varphi}\left(\mathbf{x}_i\right)+b\right)-1+\xi_i\right]-\sum_{i=1}^p \mu_i \xi_i$

(5.25)

w której mnożniki $\alpha_i$ odpowiadają ograniczeniom funkcyjnym a $\mu_i$ ograniczeniom nierównościowym nakładanym na zmienne $\xi_i$ (wzór 5.24).

Rozwiązanie powyższego problemu optymalizacyjnego zakłada w pierwszym etapie przyrównanie do zera pochodnych funkcji Lagrange'a względem $\mathbf{w}$ , $b$ oraz $\xi_i$ . Z zależności tych otrzymuje się wyrażenie wektora $\mathbf{w}$ poprzez mnożniki Lagrange'a oraz dodatkowe zależności funkcyjne, które muszą być spełnione. Po uwzględnieniu tych zależności problem pierwotny przekształca się w problem dualny zdefiniowany wyłącznie względem mnożników Lagrange'a $\alpha_i$ o następującej postaci (mnożniki $\mu_i$ zostają wyeliminowane)

$\max _{\boldsymbol{\alpha}} {Q}(\boldsymbol{\alpha})=\sum_{{i}=1}^{{p}} \alpha_{{i}}-\frac{1}{2} \sum_{{i}=1}^{{p}} \sum_{{j}=1}^{{p}} \alpha_{{i}} \alpha_{{j}} d_i d_j K\left(\mathbf{x}_i, \mathbf{x}_j\right)$

(5.26)

przy ograniczeniach $(i=1, 2,\ldots,p)$

$\begin{aligned} 0 \leq \alpha_i &\leq C \\ \sum_{i=1}^p \alpha_i d_i&=0 \end{aligned}$

(5.27)

przy wartości stałej $C$ przyjętej z góry przez użytkownika. Funkcja $K\left(\mathbf{x}_i, \mathbf{x}_j\right)$ występująca w sformułowaniu zadania dualnego jest iloczynem skalarnym funkcji wektorowej $\boldsymbol{\varphi}(\mathbf{x})=\left[\varphi_1(\mathbf{x}), \varphi_2(\mathbf{x}), \ldots, \varphi_K(\mathbf{x})\right]^T$ określonym dla wektorów $\mathbf{x}_i$ oraz $\mathbf{x}_j$

$K\left(\mathbf{x}_i, \mathbf{x}_j\right)=\boldsymbol{\varphi}^T\left(\mathbf{x}_i\right) \boldsymbol{\varphi}\left(\mathbf{x}_j\right)$

(5.28)

Iloczyn ten nazywany jest funkcją jądra (ang. kernel function). Z definicji jest to skalarna funkcja symetryczna, to znaczy $K\left(\mathbf{x}_i, \mathbf{x}_j\right) = K\left(\mathbf{x}_j, \mathbf{x}_i\right)$ . Zauważmy, że sformułowanie problemu dualnego nie zawiera ani zmiennych dopełniających ani odpowiadających im mnożników Lagrange'a. Mnożniki $\mu_i$ muszą spełniać równość $\mu_i+\alpha_i=C$ , ich iloczyn ze zmienną dopełniającą $\xi_i$ musi być równy zeru, $\mu_i \xi_i=0$ .

Rozwiązanie problemu dualnego pozwala wyznaczyć optymalne wartości mnożników Lagrange'a, na podstawie których określa się wartości optymalne wag sieci w postaci

$\mathbf{w}=\sum_{i=1}^p \alpha_i d_i \boldsymbol{\varphi}\left(\mathbf{x}_i\right)$

(5.29)

Wartość wagi polaryzacyjnej $b$ wyznacza się podobnie jak w przypadku liniowym wybierając dowolny wektor podtrzymujący $\mathbf{x}_{sv}$ dla którego $\xi_i = 0$ i stosując wzór $b= \pm 1-\mathbf{w}^T \varphi\left(\mathbf{x}_{s V}\right)$ . Po podstawieniu zależności (5.29) do wzoru (5.22) otrzymuje się ostateczne wyrażenie określające sygnał wyjściowy sieci nieliniowej SVM w postaci

$y(\mathbf{x})=\mathbf{w}^T \boldsymbol{\varphi}(\mathbf{x})+b=\sum_{i=1}^{N_{S V}} \alpha_i d_i K\left(\mathbf{x}_i, \mathbf{x}_j\right)+b$

(5.30)

Sygnał wyjściowy sieci zależy od funkcji jądra $K\left(\mathbf{x}_i, \mathbf{x}_j\right)$ a nie od funkcji aktywacji $\varphi(\mathbf{x})$ . W związku z tym wynikową strukturę sieci nieliniowej SVM można przedstawić jak na rys. 5.5.

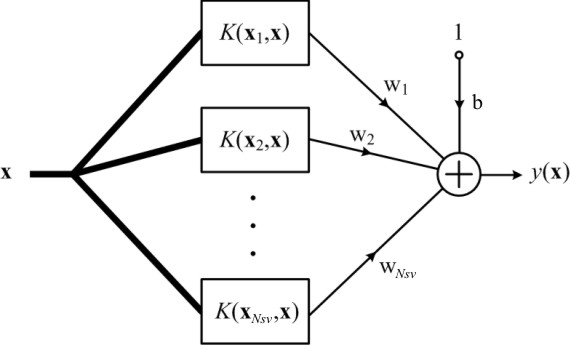
Rys. 5.5 Struktura wynikowa nieliniowej sieci SVM

O tym czy funkcja $K\left(\mathbf{x}_i, \mathbf{x}_j\right)$ jest kandydatem na jądro spełniającym warunek iloczynu skalarnego dwu bliżej nieokreślonych funkcji wektorowych $\varphi(\mathbf{x})$ i $\varphi(\mathbf{x}_j)$ decyduje spełnienie warunków twierdzenia Mercera [68]. Istnieje wiele funkcji spełniających warunek Mercera, które mogą być użyte do budowy sieci SVM. Do takich funkcji należy między jądro typu gaussowskiego, wielomianowego, funkcje sklejane oraz (przy pewnych ograniczeniach) również jądro sigmoidalne [46,59].

W tabeli 5.1 zestawiono zależności odnoszące się do najczęściej używanych jąder: liniowego, wielomianowego, radialnego oraz sigmoidalnego. Zastosowanie jądra sigmoidalnego prowadzi do powstania sieci perceptronowej o jednej warstwie ukrytej, jądra radialnego - do sieci RBF, natomiast jądra wielomianowego do sieci wielomianowej. Wszystkie te sieci zawierają jedną warstwę ukrytą. W przypadku jądra liniowego sieć jest w pełni liniowa bez warstwy ukrytej.

Tabela 5.1. Przykłady funkcji jąder

Funkcja jądra	Równanie	Uwagi
Liniowe	$K\left(\mathbf{x}_i, \mathbf{x}\right)=\mathbf{x}^T \mathbf{x}_i+\gamma$	$\gamma$ - wartość stała
Wielomianowe	$K\left(\mathbf{x}_i, \mathbf{x}\right)=\left(\mathbf{x}^T \mathbf{x}_i+\gamma\right)^q$	$q$ –stopień wielomianu
Gaussowskie	$K\left(\mathbf{x}_i, \mathbf{x}\right)=\exp \left(-\gamma\left\\|\mathbf{x}-\mathbf{x}_i\right\\|^2\right)$	$\gamma$ - wartość stała (odwrotność $\sigma^2$ )
Sigmoidalne	$K\left(\mathbf{x}_i, \mathbf{x}\right)=\operatorname{tgh}\left(\beta \mathbf{x}^T \mathbf{x}_i+\gamma\right)$	$\beta, \gamma$ - współczynniki liczbowe

Funkcje jądra dają swój wkład w definicję funkcji celu w zadaniu dualnym dla konkretnych wartości wektorów wejściowych $\mathbf{x}$ . Przy ustalonych przez użytkownika wartościach współczynników tych funkcji składniki związane z jądrem mają charakter liczbowy i rodzaj zastosowanego jądra nie ma żadnego związku z nieliniowością problemu optymalizacyjnego (problem dualny jest zawsze o postaci kwadratowej). Zauważmy, że funkcje jądra $K\left(\mathbf{x}_i, \mathbf{x}_j\right)$ są wielkościami skalarnymi i dla wszystkich możliwych kombinacji indeksów $i, j$ tworząc macierz kwadratową.

Należy podkreślić, że w sieci radialnej liczba funkcji bazowych i ich centra są automatycznie utożsamione z wektorami podtrzymującymi. Sieć SVM o radialnej funkcji jądra może więc być utożsamiona z siecią radialną RBF, choć jej ostateczna struktura jak również sposób uczenia są różne. W sieci sigmoidalnej liczba neuronów ukrytych jest określona również automatycznie przez liczbę wektorów podtrzymujących i położenia tych wektorów.

Istotnym elementem teorii sieci nieliniowej SVM jest fakt, że po zastąpieniu wektora $\mathbf{x}$ poprzez wektor $\boldsymbol{\varphi}(\mathbf{x})$ a iloczynu skalarnego $\mathbf{x}_i^T \mathbf{x}_j$ przez $K\left(\mathbf{x}_i, \mathbf{x}_j\right)$ problem uczenia można sformułować w identyczny sposób jak dla sieci liniowej, jako problem pierwotny i dualny. Rozwiązaniu podlega praktycznie problem dualny, który niezależnie od rodzaju zastosowanej sieci jest sformułowany jako zadanie programowania kwadratowego. W procesie uczenia sieci SVM początkowa liczba wektorów podtrzymujących jest zwykle równa liczbie danych uczących. W zależności od przyjętych wartości ograniczeń (wartość parametru $C$ ) złożoność sieci jest redukowana i tylko część wektorów uczących pozostaje nadal wektorami podtrzymującymi.

Na rys. 5.6 przedstawiono przykład działania klasyfikacyjnego sieci SVM o jądrze radialnym dla rozkładu danych dwuwymiarowych rozmieszczonych jak na rysunku, należących do dwu klas. Jak widać przy odpowiedniej wartości współczynnika $C$ hiperpłaszczyzna w przestrzeni cech transformuje się w nieliniową krzywą w przestrzeni oryginalnej $\mathbf{x}$ , separującą bezbłędnie obie klasy. Liczba wektorów podtrzymujących zależy od wartości $C$ . Im wyższa jego wartość tym większa kara za przekroczenie ograniczeń i w efekcie węższy margines separacji, a co za tym idzie również mniejsza liczba wektorów podtrzymujących.

Rys. 5.6 Przykłady klasyfikacji danych nieseparowalnych liniowo przy zastosowaniu sieci nieliniowej o jądrze radialnym

Przy małej wartości $C$ kara za przekroczenie ograniczeń jest niewielka i optymalne wartości wag umożliwiają klasyfikację z wieloma błędami na danych uczących.

5.3.1 Interpretacja mnożników Lagrange'a w rozwiązaniu sieci

Mnożniki Lagrange'a spełniają bardzo ważną rolę w rozwiązaniu problemu uczenia sieci SVM. Każdy mnożnik $\alpha_i$ jest stowarzyszony z odpowiadającą mu parą uczącą $(\mathbf{x}_i, d_i)$ stanowiąc współczynnik kary za niespełnienie ograniczenia (w przypadku spełnienia tego ograniczenia wartość mnożnika powinna być zerowa). Z warunków optymalności Kuhna-Tuckera problemu optymalizacyjnego sformułowanego dla sieci SVM wynikają następujące zależności [32,59]

$\begin{aligned} & \alpha_i\left[ d_i\left(\mathbf{w}^T \varphi\left(\mathbf{x}_i\right)+b\right)+\xi_i-1\right]=0 \\ & 0 \leq \alpha_i \leq C \\ & \mu_i \xi_i=0 \\ & \alpha_i+\mu_i=C \\ & \xi_i \geq 0 \end{aligned}$

(5.31)

W przypadku spełnienia ograniczenia mnożnik Lagrange'a z definicji powinien przyjąć wartość zerową eliminując wpływ danego ograniczenia na wartość minimalizowanej funkcji celu. W zależności od obliczonych wartości mnożników $\alpha_i$ możemy mieć do czynienia z 3 przypadkami.

$\alpha_i = 0$

Biorąc pod uwagę warunek Kuhna-Tuckera $\alpha_i+\mu_i=C$ wartość zmiennej dopełniającej $\mu_i=C$ . Uwzględniając zależność $\mu_i\xi_i=0$ jest oczywiste, że $\xi_i=0$ , co oznacza, że para ucząca $(\mathbf{x}_i, d_i)$ spełnia ograniczenie bez zmniejszania szerokości marginesu separacji (klasyfikacja całkowicie poprawna). Co więcej, wobec zerowej wartości $\alpha_i$ para ta nie wnosi żadnego wkładu do ukształtowanej hiperpłaszczyzny separującej.

$0 < \alpha_i < C$

Wartość mnożnika $\mu_i$ jest równa $\mu_i=C-\alpha_i$ co oznacza, że dla spełnienia warunki $\mu_i\xi_i=0$ wartość $\xi_i=0$ podobnie jak w przypadku poprzednim. Jednakże tym razem wobec niezerowej wartości $\alpha_i$ zerować się musi czynnik $d_i\left(\mathbf{w}^T \varphi\left(\mathbf{x}_i\right)+b\right)+\xi_i-1$ . Przy zerowej wartości $\xi_i$ i binarnych wartościach zadanych $d_i=\pm 1$ otrzymuje się warunek $\mathbf{w}^T \varphi\left(\mathbf{x}_i\right)+b= \pm 1$ oznaczający, że wektor $x_i$ jest wektorem podtrzymującym. Stąd wartość mnożnika z przedziału $0 < \alpha_i < C$ oznacza, że para danych uczących położona jest dokładnie na marginesie separacji (klasyfikacja poprawna).

$\alpha_i = C$

W tym przypadku wobec $\mu_i = C - \alpha_i = 0$ mamy $\xi_i \geq 0$ . Oznacza to, że dana ucząca znalazła się wewnątrz marginesu separacji lub poza tym marginesem (po niewłaściwej stronie), prowadząc bądź do błędu klasyfikacji bądź jedynie do realnego zmniejszenia szerokości marginesu. Wobec $\alpha_i \neq 0$ spełniony musi być warunek $\left[ d_i\left(\mathbf{w}^T \varphi\left(\mathbf{x}_i\right)+b\right)+\xi_i-1\right]=0$ , z którego wynika, że $\mathbf{w}^T \varphi\left(\mathbf{x}_i\right)+b=1-\xi_i$ . Wartość niezerowa $\xi_i$ oznacza więc wejście w margines separacji o wartość $\xi_i$ . Jeśli ta wartość jest mniejsza od 1 mamy do czynienia jedynie ze zmniejszeniem marginesu przy poprawnej klasyfikacji. W przeciwnym przypadku, gdy $\xi_i > 1$ popełniony zostaje błąd (punkt danych po niewłaściwej stronie marginesu separacji).

7.3.2 Problem klasyfikacji przy wielu klasach

Sieci SVM z istoty swego działania dokonują rozdziału danych na dwie klasy. W odróżnieniu od sieci klasycznych, gdzie liczba klas poddanych klasyfikacji może być dowolna, rozpoznanie wielu klas przy pomocy tej techniki wymaga przeprowadzenia wielokrotnej klasyfikacji. Do najbardziej znanych podejść należą tu metody "jeden przeciw pozostałym" i "jeden przeciw jednemu". W metodzie "jeden przeciw pozostałym" przy $M$ klasach należy skonstruować $M$ sieci, każda odpowiedzialna za rozpoznanie jednej klasy. Sieć $i$ -ta jest trenowana na danych uczących, w których przykłady $i$ -tej klasy są skojarzone z $d_i=1$ a pozostałe z $d_i = -1$ .

Przykładowo przy istnieniu 4 klas problem sprowadza się wytrenowania 4 sieci SVM, każda trenowana na innym zbiorze danych:

Sieć 1: (klasa 1: dane klasy 1), (klasa przeciwna: dane klasy 2+3+4)
Sieć 2: (klasa 1: dane klasy 2), (klasa przeciwna: dane klasy 1+3+4)
Sieć 3: (klasa 1: dane klasy 3), (klasa przeciwna: dane klasy 1+2+4)
Sieć 4: (klasa 1: dane klasy 4), (klasa przeciwna: dane klasy 1+2+3)

Po wytrenowaniu wszystkich sieci następuje etap odtwarzania, w którym ten sam wektor $\mathbf{x}$ jest podawany na każdą sieć SVM. Określane są sygnały wyjściowe $M$ funkcji decyzyjnych) wszystkich wytrenowanych sieci SVM (w przypadku klasy złożonej zwycięstwa przypisuje się do każdej klasy składowej)

$\begin{gathered} y_1(\mathbf{x})=\mathbf{w}_1^T \varphi(\mathbf{x})+b_1 \\ y_2(\mathbf{x})=\mathbf{w}_2^T \varphi(\mathbf{x})+b_2 \\ \ldots \\ y_M(\mathbf{x})=\mathbf{w}_M^T \varphi(\mathbf{x})+b_M \end{gathered}$

(5.32)

Wektor $\mathbf{x}$ jest następnie zaliczany do klasy o największej wartości funkcji decyzyjnej $y_i(\mathbf{x})$ , poprzez głosowanie większościowe.

Innym równie często stosowanym rozwiązaniem jest metoda "jeden przeciw jednemu" [46]. W metodzie tej konstruuje się $M(M-1)/2$ klasyfikatorów typu SVM, rozróżniających za każdym razem 2 klasy danych ze zbioru uczącego, kolejno parowanych ze sobą. Przykładowo przy 4 klasach poszczególne sieci będą trenowane na następujących zbiorach danych (6 sieci SVM)

Sieć 1: klasa 1 (dane klasy 1), klasa 2 (dane klasy 2)
Sieć 2: klasa 1 (dane klasy 2), klasa 2 (dane klasy 3)
Sieć 3: klasa 1 (dane klasy 3), klasa 2 (dane klasy 4)
Sieć 4: klasa 1 (dane klasy 2), klasa 2 (dane klasy 3)
Sieć 5: klasa 1 (dane klasy 2), klasa 2 (dane klasy 4)
Sieć 6: klasa 1 (dane klasy 3), klasa 2 (dane klasy 4)

Po wytrenowaniu wszystkich $M(M-1)/2$ sieci można przystąpić do właściwej klasyfikacji przy założeniu konkretnej wartości wektora $\mathbf{x}$ . Oznaczmy równanie decyzyjne sieci SVM rozróżniającej między klasą $i$ -tą a $j$ -tą dla danych wejściowych opisanych wektorem $\mathbf{x}$ w postaci

$y_{i j}(\mathbf{x})=\mathbf{w}_{i j}^T \varphi(\mathbf{x})+b_{i j}$

(5.33)

Jeśli $\operatorname{sgn}\left(y_{i j}(\mathbf{x})\right)$ wskazuje na $i$ -tą klasę, należy zwiększyć o jeden sumę wskazań do tej klasy. W przeciwnym wypadku zwiększyć o jeden sumę wskazań do klasy $j$ -tej w głosowaniu. Klasa o największej sumie zwycięstw wśród M(M-1)/2 sieci jest uważana za zwycięską (wektor $\mathbf{x}$ zalicza się ostatecznie do tej klasy).

W ostatnich latach zaproponowano wiele nowych, równie skutecznych podejść do rozpoznawania wielu klas, pozwalających na rozwiązanie problemu w jednej strukturze SVM, przy uwzględnieniu wszystkich danych uczących na raz i z zastosowaniem dekompozycji zbioru uczącego na mniejsze podzbiory dla przyśpieszenia procedury uczenia. Do takich metod należą między innymi metoda Cramera i Singera [9] oraz metoda C. Hsu i C. Lina [28].