Podręcznik

1. Sieci samoorganizujące poprzez współzawodnictwo

1.3. Odwzorowanie Sammona

Rozkład danych wielowymiarowych uzyskanych w sieci samoorganizującej może być przedstawiony na płaszczyźnie lub w przestrzeni trójwymiarowej przy zastosowaniu rzutowań innych niż mapa Kohonena. Jednym ze znanych jest nieliniowe odwzorowanie Sammona [57]. Odwzorowanie to pozwala na rzutowanie danych z dowolnej przestrzeni N-wymiarowej w przestrzeń M-wymiarową (np. M=2 lub M=3) zachowując podstawowe cechy rozkładu danych z oryginalnej przestrzeni wielowymiarowej.

Niech będzie danych n wektorów N-wymiarowych x_i (i=1, 2, …n). Odpowiednio do nich definiuje się n wektorów w przestrzeni M-wymiarowej oznaczonych przez y_i. Odległości między poszczególnymi wektorami w przestrzeni N-wymiarowej oznaczane będą przez $d_{i j}^*=d\left(\mathbf{x}_i, \mathbf{x}_j\right)$ a w przestrzeni M-wymiarowej przez $d_{i j}=d\left(\mathbf{y}_i, \mathbf{y}_j\right)$ . W określeniu odległości między wektorami można zastosować dowolną metrykę, w szczególności euklidesową. Zadanie odwzorowania nieliniowego Sammona polega na takim doborze wektorów y, aby zminimalizować funkcję błędu E zdefiniowaną wzorem [57]

$\min E=\frac{1}{c} \sum_{i < j}^n \frac{\left(d_{i j}^*-d_{i j}\right)^2}{d_{i j}^*}$

(7.19)

gdzie

$c=\sum_{i < j}^n d_{i j}^*$

(7.20)

$d_{i j}=\sqrt{\sum_{k=1}^M\left(y_{i k}-y_{j k}\right)^2}$

(7.21)

W zależnościach tych y_ij oznacza j-tą składową wektora y_i. W minimalizacji funkcji błędu (7.19) Sammon zastosował uproszczoną metodę optymalizacyjną Newtona, która pozwala wyrazić rozwiązanie z kroku na krok w sposób rekurencyjny w postaci

$y_{i j}(k+1)=y_{i j}(k)-\eta \Delta_{i j}(k)$

(7.22)

$\Delta_{i j}(k)=\frac{\partial E / \partial y_{i j}}{\left|\partial^2 E / \partial y_{i j}^2\right|}$

(7.23)

Wzór wyrażający poprawkę reprezentuje iloraz odpowiedniej składowej gradientu przez diagonalny składnik hesjanu, określony w k-tej iteracji. Współczynnik $\eta$ jest odpowiednikiem stałej uczenia i przyjmowany jest z zakresu [0,3, 0,4]. Przy definicji funkcji błędu w postaci (7.19) odpowiednie składowe gradientu i hesjanu opisane są wzorami [57]

$\frac{\partial E}{\partial y_{i j}}=-\frac{2}{C} \sum_{\substack{p=1 \\ p \neq i}}^n\left[\frac{d_{i p}^*-d_{i p}}{d_{i p} d_{i p}^*}\right]\left(y_{i j}-y_{p j}\right)$

(7.24)

$\frac{\partial^2 E}{\partial y_{i j}^2}=-\frac{2}{c} \sum_{\substack{p=1 \\ p \neq i}}^n \frac{1}{d_{i p} d_{i p}^*}\left[\left(d_{i p}^*-d_{i p}\right)-\frac{\left(y_{i j}^*-y_{p j}\right)^2}{d_{i p}}\left(1+\frac{d_{i p}^*-d_{i p}}{d_{i p}}\right)\right]$

(7.25)

W wyniku wielu iteracji składowe wektorów y_i przyjmują wartości ostateczne minimalizujące wartość zdefiniowanej na wstępie funkcji błędu.

Na rys. 7.9 przedstawiono rzutowanie Sammona dla tych samych danych dotyczących obciążeń elektroenergetycznych w Polskim Systemie Elektroenergetycznym (PSE) przedstawionych na mapie Kohonena. Uwzględniono rodzaje obciążeń odpowiadających czterem porom roku (kolor zielony – wiosna, czerwony – lato, magenta – jesień oraz niebieski – zima). Dane rzeczywiste obciążeń dotyczą wektorów 24-wymiarowych (obciążenia 24 godzin doby).

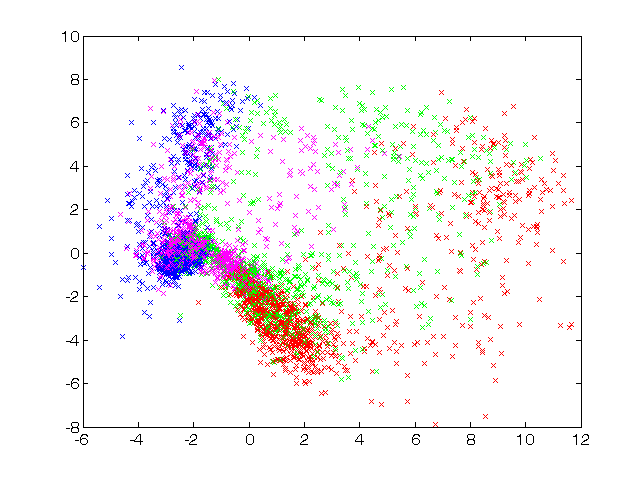
Rys. 7.9. Rozkład danych 24-wymiarowych obciążeń elektroenergetycznych w PSE zrzutowany na płaszczyznę przy użyciu odwzorowania Sammona

Zauważmy, że również przy tym rzutowaniu dane dotyczące lata i zimy są odległe od siebie, podczas gdy te związane z wiosną i jesienią są bliskie sobie i położone na mapie w bliskim sąsiedztwie. Ponadto charakterystyczne jest, że dane dotyczące zimy są stosunkowo mało rozproszone w stosunku do innych pór roku, natomiast dane wiosenne charakteryzują się rozproszeniem największym (duże różnice między najwyższą i najniższą temperatura powodują duże zróżnicowanie w poborze energii elektrycznej).