Podręcznik
3. Ślepa separacja sygnałów
3.1. Wprowadzenie
Oryginalne rozwiązanie Heraulta-Juttena dotyczyło problemu separacji sygnałów \( s_j (t) \) zmiennych w czasie na podstawie informacji zawartej w ich liniowej superpozycji. Przyjmiemy za ich twórcami, że danych jest n niezależnych (nieznanych) sygnałów \( s_j (t) \) oraz macierz mieszająca \( \mathbf{A} \) (również nieznana) o wymiarze \( n \times n \). Dla pomiarów dostępne są jedynie sygnały \( x_i (t) \) będące liniową superpozycją \( s_j (t) \) przy czym [8]
| \(x_i(t)=\sum_{j=1}^n a_{i j} s_j\) | (9.1) |
dla \( i = 1, 2, \ldots, n \). Główna trudność polega na tym, że zarówno \( a_{ij} (t) \) jak i \( s_j (t) \) nie są znane. Przy założeniu statystycznej niezależności sygnałów J. Herault i C. Jutten zaproponowali rozwiązanie problemu z wykorzystaniem sieci neuronowej [8].
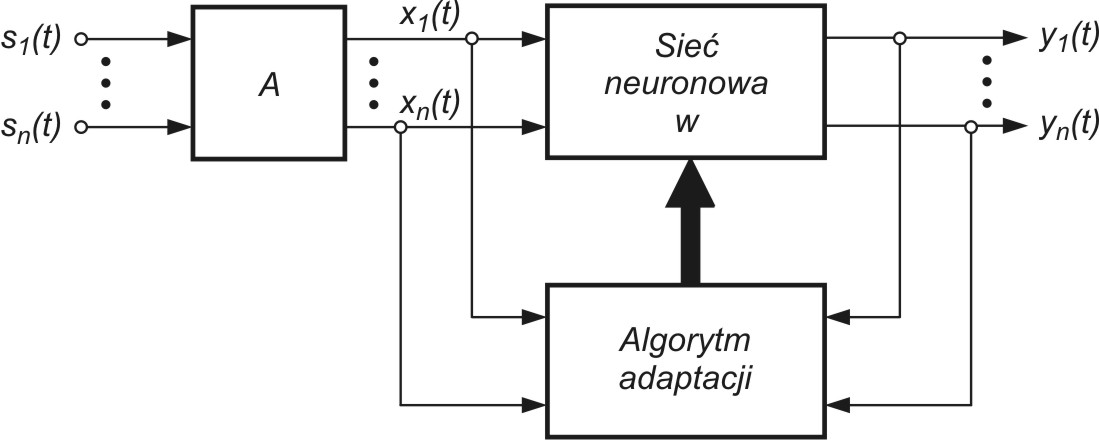
Schemat ogólny włączenia tej sieci w system pomiarowy przedstawiono na rys. 9.1. Istotnym założeniem w ich rozwiązaniu jest statystyczna niezależność sygnałów źródłowych.