Podręcznik
2. Metody oceny jakości rozwiązań
2.2. Metody oceny jakości rozwiązań w zadaniach klasyfikacji
W przypadku klasyfikacji miary jakości klasyfikatora są zdefiniowane na podstawie zgodności estymowanej etykiety klasy z etykietą rzeczywistą (prawdziwą). Najbardziej reprezentatywnym sposobem prezentacji wyników jest tutaj zastosowanie macierzy pomyłek, zwanej również macierzą niezgodności klasowej lub macierzą pomyłek (ang. confusion matrix), w której elementy wierszy reprezentują liczbę wzorców należących do kolejnych klas, a elementy kolumn – liczbę wzorców rozpoznanych przez klasyfikator jako dana klasa [65]. Przykład takiej macierzy dla trzech klas przedstawiono w tabeli 12.1. Elementy diagonalne macierzy reprezentują liczbę poprawnie rozpoznanych wzorców. Każdy element pozadiagonalny macierzy reprezentuje błędne rozpoznanie. Element ij-ty macierzy określa liczbę przypadków klasy i-tej rozpoznanych jako klasa j-ta. Klasa pierwsza jest reprezentowana przez pierwszy wiersz, klasa druga przez drugi a klasa trzecia przez wiersz trzeci.
Tabela 12.1 Przykład prezentacji wyników klasyfikacji wzorców 3 klas w postaci macierzy rozkładu klas
|
|
Klasa 1 |
Klasa 2 |
Klasa 3 |
|
Klasa 1 |
95 |
3 |
12 |
|
Klasa 2 |
8 |
20 |
2 |
|
Klasa 3 |
6 |
0 |
80 |
Przykładowo spośród 110 przypadków klasy pierwszej 95 zostało rozpoznanych poprawnie, 3 rozpoznanych błędnie jako klasa druga a 12 jako klasa trzecia.
12.2.1 Miary jakości klasyfikatora
Na podstawie wyników klasyfikacji przedstawionych w macierzy rozkładu klas można stworzyć wiele różnych wskaźników jakości klasyfikatora. Najbardziej ogólnym wskaźnikiem jest średni błąd względny w którym odnosi się liczbę klasyfikacji błędnych do liczby wszystkich przypadków poddanych badaniu. Błąd ten można zdefiniować na dwa sposoby: błąd średni dla całego zbioru bez uwzględnienia liczebności klas oraz z ich uwzględnieniem. Oznaczając elementy macierzy rozkładu klas przez aij, oba rodzaje błędów można zdefiniować w następujący sposób.
-
Błąd średni bez uwzględnienia liczebności klas
| \( \varepsilon_{w 1}=\frac{\sum_{i \neq j} a_{i j}}{\sum_{i, j} a_{i j}} \) | (12.12) |
-
Błąd średni ważony z uwzględnieniem liczebności klas
| \( \varepsilon_{w 2}=\frac{1}{K} \sum_{i=1}^K \frac{\sum_{j=1, j \neq i}^K a_{i j}}{K_i} \) | (12.13) |
We wzorach tych K oznacza liczbę klas, a \(K_i\) liczbę elementów \(i\)-tej klasy. W przypadku równej liczebności wszystkich klas oba wskaźniki przyjmują identyczne wartości. Przy nierównych populacjach klas wskaźnik drugi jest bardziej wymagający. Przykładowo dla danych z tabeli 12.1 \(\varepsilon_{w1}=31/226=0.137\), podczas gdy \(\varepsilon_{w2}=(15/110+10/30+6/86)/3=0.180\).
Wskaźniki zdefiniowane powyżej nie odzwierciedlają problemów występujących w przypadku dużego niezrównoważenia klas. Przykładowo, jeśli w zbiorze danych 99% danych należy do klasy pierwszej a tylko 1% do klasy drugiej (rzadkiej), wówczas przy pełnym rozpoznaniu klasy pierwszej i zerowej skuteczności rozpoznania klasy rzadkiej średni błąd rozpoznania \( \varepsilon_{w1}=1\% \), co jest rezultatem zwykle satysfakcjonującym z ogólnego punktu widzenia ale zupełnie nie odzwierciedlającym problemu (1% klasy rzadkiej może reprezentować właśnie te przypadki, które chcemy wykryć w populacji przypadków normalnych, np. chorobę nowotworową w grupie badanych pacjentów). Problem oceny klasyfikatora stosowanego do przypadków rzadkich wymaga innego podejścia do definicji miar jakości, gdyż przypomina szukanie igły w stogu siana.
Rozpatrzmy przypadek klasyfikacji danych należących do dwu klas. Klasę rzadką oznaczymy symbolem + a większościową symbolem –. W takim przypadku macierz rozkładu klasowego może być przedstawiona w postaci jak w tabeli 12.2 [49,65].
Tabela 12.2 Oznaczenia stosowane w macierzy rozkładu klas (+ oznacza klasę rzadką, natomiast – klasę większościową, reprezentującą pozostałe przypadki)
|
|
Klasa + |
Klasa – |
|
Klasa + |
a++ (TP) |
a+– (FN) |
|
Klasa – |
a–+ (FP) |
a– – (TN) |
Element a++ macierzy oznacza liczbę prawdziwie rozpoznanych przypadków rzadkich (ang. True Positive – TP), element a+– oznacza liczbę przypadków rzadkich rozpoznanych jako większościowe (ang. False Negative – FN), element a–+ oznacza liczbę przypadków większościowych rozpoznanych jako rzadkie (ang. False Positive – FP), a element a– – oznacza liczbę prawdziwie rozpoznanych przypadków większościowych (ang. True Negative – TN). Na bazie tych oznaczeń definiuje się szereg wskaźników jakości szerzej naświetlających problem klasyfikacji w przypadku klas rzadkich [45]. Pierwszym z nich jest czułość oznaczana zwykle symbolem TPR (ang. True Positive Rate), definiowana jako stosunek liczby poprawnie rozpoznanych przypadków rzadkich do liczby wszystkich przypadków rzadkich
| \( TPR = \frac{TP}{TP+FN} \) |
(12.14) |
Drugim ważnym parametrem jest specyficzność oznaczana symbolem TNR (ang. True Negative Rate), definiowana jako stosunek liczby poprawnie rozpoznanych przypadków większościowych do liczby wszystkich przypadków większościowych
| \( TNR = \frac{TN}{TN+FP} \) | (12.15) |
Inną miarą jest wskaźnik rozpoznań fałszywie pozytywnych oznaczany symbolem FPR (ang. False Positive Rate) zdefiniowany jako stosunek liczby przypadków większościowych sklasyfikowanych jako rzadkie do liczby wszystkich przypadków większościowych
| \( FPR = \frac{FP}{TN+FP} \) | (12.16) |
Miara ta jest znana również jako wskaźnik fałszywych alarmów FA (ang. False Alarm), określający względny udział błędnych kwalifikacji przypadków większościowych jako rzadkie (np. uznanie pacjenta zdrowego za chorego). Wskaźnik ten jest ściśle powiązany ze specyficznością TNR
| \( FA=FPR=\frac{FP}{FP+TN}=1-TNR \) | (12.17) |
Analogicznie definiuje się wskaźnik rozpoznań fałszywie negatywnych (szczególnie niebezpiecznych) oznaczany symbolem FNR (ang. False Negative Rate). Jest on zdefiniowany jako stosunek liczby przypadków rzadkich sklasyfikowanych jako większościowe do liczby wszystkich przypadków rzadkich
| \( FNR = \frac{FN}{TP+FN} \) | (12.18) |
Dwa dodatkowe wskaźniki definiują wartości prognostyczne metody. Dodatnia wartość prognostyczna PPV reprezentująca precyzję rozpoznawania przypadków rzadkich (ang. Positive Predictivity Value) określa jaka część przypadków zdiagnozowanych jako rzadkie (TP) jest rzeczywiście rzadka (percepcja rozpoznawania klasy rzadkiej)
| \( PPV = \frac{TP}{TP+FP} \) | (12.19) |
Ujemna wartość prognostyczna NPV (ang. Negative Predictivity Value) określa jaka część przypadków zdiagnozowanych jako większościowa (TN) jest rzeczywiście większościowa (percepcja rozpoznawania klasy większościowej)
| \( NPV = \frac{TN}{TN+FN} \) | (12.20) |
Ważną praktycznie miarą jakości systemu klasyfikacyjnego jest precyzja klasowa klasyfikatora. Jest ona definiowana jako stosunek prawdziwej liczby rozpoznanych przypadków danej klasy do wszystkich przypadków rozpoznanych przez klasyfikator jako dana klasa. Miara ta dotyczy każdej klasy, w tym większościowej i rzadkiej, oznaczonych jako PPV i NPV
Inną miarą uniwersalną systemu klasyfikacyjnego jest F1. Definiowana jest dla każdej klasy oddzielnie na podstawie precyzji oraz czułości klasowej. Oznaczając precyzję rozpoznania klasy k-tej przez \(\operatorname{Prec}(k)\) i czułość rozpoznania klasy przez \(\operatorname{Sens}(k) \) miara \( \operatorname{F1}(k) \) jest zdefiniowana w postaci
| \( \operatorname{F1}(k)=\frac{\operatorname{Prec}(k) * \operatorname{Sens}(k)}{0.5(\operatorname{Prec}(k)+\operatorname{Sens}(k))} \) | 12.21 |
Średnia dokładność prognozy ACC (ang. ACCuracy) określająca procent dobrze sklasyfikowanych przypadków może być zdefiniowana wzorem
| \( AC=\frac{TP+TN}{TP+TN+FP+FN} \) | (12.22) |
Oznacza ona liczbę prawidłowo sklasyfikowanych przypadków (rzadkich i większościowych) odniesioną do liczby wszystkich przypadków poddanych klasyfikacji. Miara ta jest ściśle związana ze średnim błędem względnym \(\varepsilon_{w1}\) zdefiniowanym wcześniej (zależność 12.12)
| \( \varepsilon_{w 1}=1-ACC=\frac{FP+FN}{TP+TN+FP+FN} \) | (12.23) |
Przedstawione powyżej miary jakości charakteryzują klasyfikator z różnych punktów widzenia. Maksymalizacja jednego wskaźnika jest często sprzężona z pogorszeniem innego.
W przypadku większej liczby klas przyjmuje się porównanie wybranej klasy z pozostałymi traktowanymi jako grupa wspólna (klasa zbiorowa). W ten sposób problem oceny sprowadza się do zadania 2-klasowego.
12.2.2 Charakterystyka ROC
Ważnym elementem oceny klasyfikatora jest porównanie jego działania z klasyfikatorem losowym [49,65]. Porównanie takie umożliwia reprezentacja graficzna wyników w postaci charakterystyki ROC (ang. Receiver Operating Characteristics). Krzywa ROC przedstawia relację między miarą TPR (oś pionowa y) a miarą FPR (oś pozioma x). Każdy punkt krzywej odpowiada innemu doborowi parametrów modelu klasyfikatora. Dwa typy możliwych przebiegów krzywej ROC dla klasyfikatorów K1 oraz K2 w porównaniu z klasyfikatorem losowym Kr (klasyfikacja poprzez losowanie) przedstawione są na rys. 12.1.
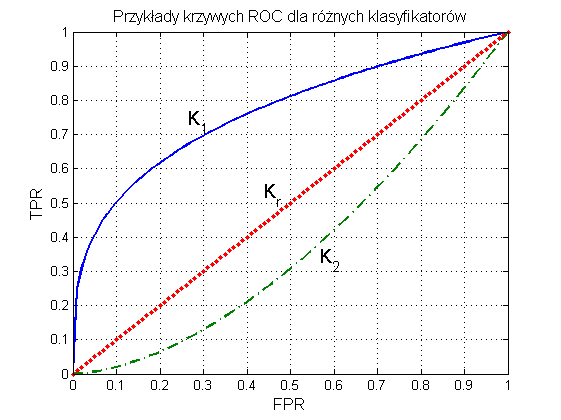
W krzywej ROC można wyróżnić kilka istotnych punktów [65].
-
(TPR=0, FPR=0) – klasyfikator kwalifikuje każdy przykład jako klasę większościową
-
(TPR=1, FPR=1) – klasyfikator kwalifikuje każdy przykład jako klasę rzadką
-
(TPR=1, FPR=0) – model idealny, rozpoznający bezbłędnie wszystkie przypadki
-
punkty (TPR, FPR) położone na prostej diagonalnej oznaczają klasyfikację całkowicie losową.
Dobry klasyfikator powinien mieć krzywą ROC położoną tak blisko jak to możliwe lewego górnego punktu o współrzędnych (0, 1). Miara jakości klasyfikatora może być oceniana na podstawie pola powierzchni SROC pod krzywą ROC. Pole powierzchni SROC=1 oznacza klasyfikator idealny. Wartość pola SROC=0.5 oznacza klasyfikację losową (rozwiązanie klasyfikatora bezsensowne). Im SROC jest bliższe jedności, tym lepsza jest ocena takiego rozwiązania modelu klasyfikacyjnego. Miara nosi popularną nazwę AUC (Area Under Curve).
Aby utworzyć krzywą ROC należy dysponować sygnałem wyjściowym klasyfikatora w postaci ciągłej (przed binaryzacją). Może to być aktualna wartość prawdopodobieństwa w klasyfikatorze Bayes’a, bezpośrednia wartość funkcji sigmoidalnej w klasyfikatorze MLP, wartość sumy wagowej neuronu wyjściowego sieci RBF czy wartość ciągła y(x) wytworzona w klasyfikatorze SVM. Procedurę tworzenia krzywej ROC można przedstawić w następujących punktach.
-
Ustaw wyniki klasyfikacji (rekordy danych testowych) w kolejności rosnącej (od najmniejszego do największego) sygnału wyjściowego klasyfikatora.
-
Wyselekcjonuj rekord o najmniejszej wartości sygnału. Sklasyfikuj wybrany rekord i wszystkie powyżej niego jako klasę rzadką (oznaczenie +). To oznacza w rzeczywistości przyjęcie, że wszystkie rekordy danych należą do klasy rzadkiej.
-
Przesuń się o jeden rekord w górę i sklasyfikuj wybrany rekord oraz wszystkie powyżej niego jako klasę rzadką, natomiast wszystkie poniżej niego jako klasę większościową (oznaczenie –). Dla każdego przypadku określ miary jakości w postaci wskaźników TP, FP, TN, FN, a następnie TPR oraz FPR.
-
Powtórz krok 3 dla wszystkich kolejnych rekordów, określając wartości wymienionych wyżej miar jakości.
-
Wykreśl otrzymaną zależność TPR=f(FPR), stanowiąca krzywą ROC.
-
Wyznacz pole powierzchni AUC pod krzywą ROC.
Charakterystyka ROC pozwala w prosty sposób porównać rozwiązania różnych rozwiązań systemu klasyfikacyjnego 2 klas. Istotna jest przy tym wartość pola pod krzywą ROC, tzw. AUC. Jest ona zawsze z przedziału [ 0, 1]. Im wyższa wartość AUC, tym lepsze jest rozwiązanie.
Procedurę wyznaczania krzywej ROC zilustrujemy przykładem dla wyników dwu różnych klasyfikatorów.
W pierwszym przypadku wyniki działania modelu na danych testujących przedstawiono w tabeli 12.3, w której wiersz pierwszy oznacza prawdziwą przynależność do klasy, a wiersz drugi sygnał wyjściowy klasyfikatora (przed poddaniem działaniu funkcji dyskryminującej klas).
Tabela 12.3 Wyniki testowania klasyfikatora pierwszego
|
Klasa |
+ |
– |
– |
+ |
– |
+ |
– |
+ |
|
Sygnał wyjściowy |
0.1 |
0.2 |
0.3 |
0.4 |
0.6 |
0.8 |
0.9 |
1.0 |
Stosując procedurę tworzenia charakterystyki ROC otrzymuje się wyniki przedstawione w tabeli 12.4.
Tabela 12.4 Ilustracja kolejnych etapów tworzenia charakterystyki ROC dla klasyfikatora pierwszego
|
Klasa |
+ |
– |
– |
+ |
– |
+ |
– |
+ |
|
Sygnał wyjściowy |
0.1 |
0.2 |
0.3 |
0.4 |
0.6 |
0.8 |
0.9 |
1.0 |
|
TP |
4 |
3 |
3 |
3 |
2 |
2 |
1 |
1 |
|
FP |
4 |
4 |
3 |
2 |
2 |
1 |
1 |
0 |
|
TN |
0 |
0 |
1 |
2 |
2 |
3 |
3 |
4 |
|
FN |
0 |
1 |
1 |
1 |
2 |
2 |
3 |
3 |
|
TPR |
1 |
3/4 |
3/4 |
3/4 |
2/4 |
2/4 |
1/4 |
1/4 |
|
FPR |
1 |
1 |
3/4 |
2/4 |
2/4 |
1/4 |
1/4 |
0 |
Na rys. 12.2 przedstawiono graficzną postać charakterystyki ROC. Pole powierzchni pod krzywą AUC=SROC wynosi 0.56. Jakość klasyfikatora jest więc jedynie nieznacznie lepsza od klasyfikatora losowego dla którego to pole wynosi 0.5. Jest to również uwidocznione na rysunku, gdzie prosta przerywana oznacza ROC dla klasyfikatora losowego.
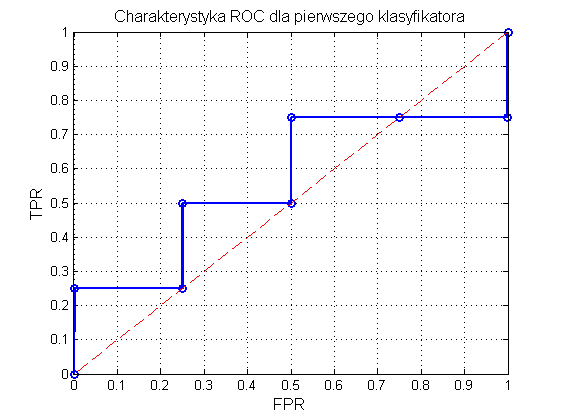
Rys. 12.2 Charakterystyka ROC klasyfikatora z przykładu pierwszego
Dla porównania w tabeli 12.5 przedstawiono wyniki klasyfikacji innego klasyfikatora oraz obliczenia dotyczące miar jakości służące do wyznaczenia krzywej ROC.
Tabela 12.5 Ilustracja kolejnych etapów tworzenia charakterystyki ROC dla klasyfikatora drugiego
|
Klasa |
– |
– |
– |
+ |
– |
+ |
+ |
+ |
|
Sygnał wyjściowy |
0.1 |
0.3 |
0.4 |
0.5 |
0.7 |
0.8 |
0.9 |
1.0 |
|
TP |
4 |
4 |
4 |
4 |
3 |
3 |
2 |
1 |
|
FP |
4 |
3 |
2 |
1 |
1 |
0 |
0 |
0 |
|
TN |
0 |
1 |
2 |
3 |
3 |
4 |
4 |
4 |
|
FN |
0 |
0 |
0 |
0 |
1 |
1 |
2 |
3 |
|
TPR |
1 |
1 |
1 |
1 |
3/4 |
3/4 |
2/4 |
1/4 |
|
FPR |
1 |
3/4 |
2/4 |
1/4 |
1/4 |
0 |
0 |
0 |
Na rys. 12.3 przedstawiono graficzną postać charakterystyki ROC odpowiadającej wynikom zawartym w tabeli 12.4. Pole powierzchni pod krzywą AUC=SROC wynosi tym razem 0.94, a więc jest bliskie jedności. Jakość klasyfikatora jest zdecydowanie lepsza od klasyfikatora losowego.
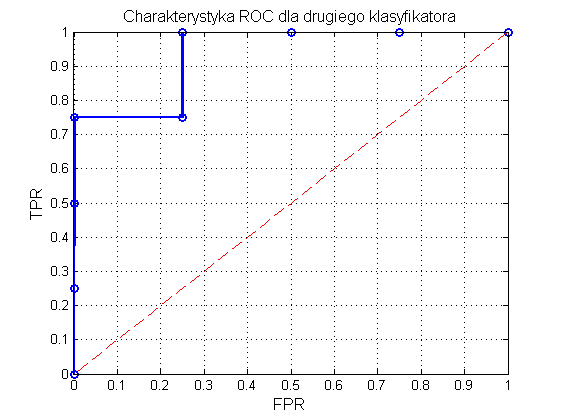
Program Matlab zawiera gotowe funkcje do wykreślania charakterystyki ROC i obliczania wartości AUC. Przykład takiego programu dla danych zawartych w tabeli podany jest poniżej.
Tabela 12.6 Dane do utworzenia krzywej ROC i obliczenia wartości AUC
|
Klasa |
– |
– |
+ |
– |
+ |
+ |
+ |
+ |
– |
+ |
+ |
|
Sygnał wyjściowy |
0.1 |
0.2 |
0.3 |
0.35 |
0.45 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1 |
y=[0.1 0.2 0.3 0.35 0.45 0.5 0.6 0.7 0.8 0.9 1]
d=[0 0 1 0 1 1 1 1 0 1 1]
[tpr,fpr,th]=roc(d,y);
figure(1), plot(fpr,tpr)
grid, xlabel('FPR'),ylabel('TPR'), title ('ROC')
[X,Y,T,AUC] = perfcurve(d,y,1)
figure(2), plotroc(d,y), grid
W wyniku uzyskuje się AUC=0.7857.