Podręcznik
4. Prognozowanie obciążeń 24-godzinnych w systemie elektroenergetycznym z użyciem zespołu sieci neuronowych
4.3. Integracja zespołu predyktorów
Każdy z zastosowanych predyktorów neuronowych wykonuje identyczne zadanie predykcji szeregu liczbowego odpowiadającego przewidywanym obciążeniom 24 godzin dnia następnego przy wykorzystaniu tej samej bazy danych obciążeń z przeszłości. Wyjściem każdego z nich jest 24-elementowy wektor x przewidywanych obciążeń. Na ich podstawie integrator (rys. 14.3) ma za zadanie wytworzyć ostateczną postać tego 24-godzinnego wzorca obciążeń na dzień następny, najlepiej odzwierciedlającego przyszłe zapotrzebowanie na moc [47].
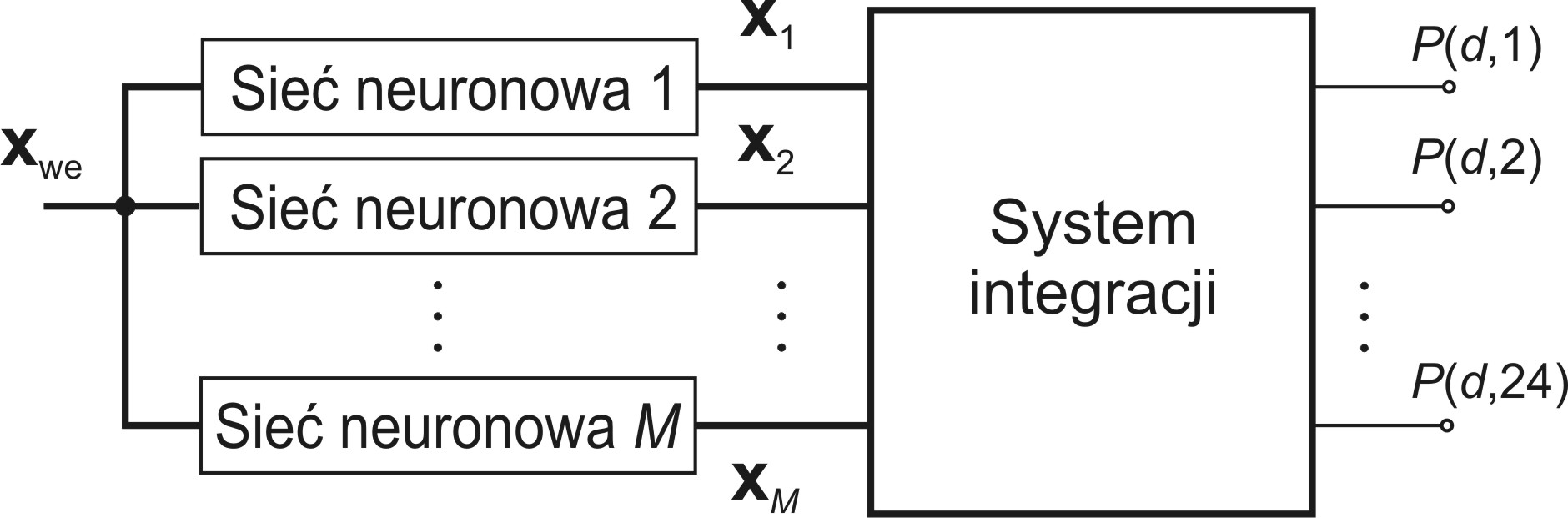
W pracy przedstawimy różne elementy przetwarzania danych w integracji, w tym uśrednianie ważone, ślepą separację sygnałów, zastosowanie dodatkowej sieci neuronowej jako integratora, czy integrację dynamiczną.
14.3.1 Integracja poprzez uśrednianie ważone
Integracja poprzez uśrednianie polega na przyjęciu prognozy końcowej jako średniej z wyników wszystkich predyktorów tworzących zespół. Zwykłe uśrednianie prowadzi do poprawy wyników, jeśli wszystkie modele indywidualne mają porównywaną dokładność, co jest w praktyce zjawiskiem rzadkim. W efekcie wynik zespołu może być gorszy niż najlepszy wynik indywidualny.
W przypadku nierównej jakości poszczególnych klasyfikatorów dużo lepsze wyniki uzyskuje się poprzez uśrednianie ważone dla każdej godziny podlegającej predykcji. W tym rozwiązaniu przy \(M\) predyktorach tworzących zespół określa się wielkość wyjściową zespołu \(y_i(\mathbf{x})\) dla \(i\)-tej godziny jako średnia ważoną wyników predyktorów indywidualnych dla tej godziny
| \( y_i\left(\mathbf{x}_{w e}\right)=\sum_{k=1}^M w_{k i} x_{k i} \) | (14.7) |
w którym \(w_{ki}\) jest wagą z jaką \(k\)-ty klasyfikator jest uwzględniany przy predykcji obciążenia dla \(i\)-tej godziny, natomiast \(x_{ki}\) jest wartością predykcji \(k\)-tego predyktora dla \(i\)-tej godziny (sygnał \(i\)-tego wyjścia predyktora).
Wartości wag \(w_{ki}\) mogą być wyznaczane w różny sposób, uwzględniający jakość poszczególnych członków zespołu. Do typowych rozwiązań należy
| \( w_{k i}=\frac{\eta_{k i}^m}{\sum_{j=1}^M \eta_{k i}^m} \) | (14.8) |
gdzie \( \eta_{k i}^m \) oznacza wskaźnik jakości (np. dokładność w sensie MAPE, MAE, RMSE) \(k\)-tego predyktora przy prognozie obciążenia dla \(i\)-tej godziny na danych uczących, \(m\) – wykładnik różnicujący wpływ poszczególnych jednostek zespołu na wynik działania zespołu (np. \(m = 1, 2, \ldots \)). Można zastosować również w integracji zespołu wzór wykorzystujący funkcję logarytmiczną [36]
| \( w_{k i}=\lg \left(\frac{\eta_{k i}}{1-\eta_{k i}}\right) \) | (14.9) |
14.3.2 Integracja przy zastosowaniu BSS
W integracji zespołu wykorzystującej metodę ślepej separacji sygnałów (BSS) [8] wszystkie 24-elementowe wektory \( \mathbf{x}_i \) prognozowane przez członków zespołu dla kolejnych \(q\) dni użytych w uczeniu (wytworzone przez poszczególne sieci neuronowe) tworzą dane uczące opisane macierzą \( \mathbf{X} \subset \mathbf{R}^{M \times p} \), w której \(p=24q\) natomiast \(M\) jest liczbą predyktorów. Sygnały opisane tą macierzą podlegają ślepej separacji mającej na celu określenie \(M\) składników niezależnych. Operację BSS opisuje zależność liniowa [48]
| \( \mathbf{Y}=\mathbf{W X} \) | (14.10) |
w której \(\mathbf{W}\) jest macierzą kwadratową o wymiarze \(M\), \( \mathbf{W} \subset \mathbf{R}^{M \times M} \). Każdy wiersz macierzy \(\mathbf{Y}\) reprezentuje składniki niezależne rozkładu macierzy \(\mathbf{X}\). Część z tych składników zawiera istotną informację dotyczącą rozkładu obciążeń, natomiast pozostała część może reprezentować nieregularności występujące w rozkładach dziennych obciążeń (na przykład wynik gwałtownych zaburzeń pogodowych, nieoczekiwanych wydarzeń wpływających na pobór mocy itp.), które są traktowane jako szum pomiarowy. Eliminacja składników szumowych „odkrywa” istotne elementy informacji i umożliwia odtworzenie wektora prognozowanych obciążeń pozbawionego wpływu tych nieregularności. Rekonstrukcja macierzy \(\mathbf{X}\) (tzw. deflacja) na podstawie jedynie istotnych składników odbywa się według wzoru
| \( \hat{\mathbf{X}}=\mathbf{W}^{-1} \hat{\mathbf{Y}} \) | (14.11) |
W równaniu tym \( \hat{\mathbf{X}} \) oznacza zrekonstruowaną macierz \( \mathbf{X} \) a \( \hat{\mathbf{Y}} \) - macierz \( \mathbf{Y} \) zmodyfikowaną w ten sposób, że wiersze odpowiadające składnikom szumowym zostały zastąpione przez zera. Problemem jest wybór tych składników „szumowych” (podlegających eliminacji). W praktyce przy wystąpieniu wątpliwości można stworzyć wiele rekonstrukcji sygnałów pomijając różne składniki traktowane jako szumowe, wybierając ostatecznie to rozwiązanie, które zapewnia najlepsze wyniki na danych uczących. W wyniku takiej rekonstrukcji odtworzone zostają wszystkie \(M\) kanały predykcji. Ostateczna integracja przeprowadzona na przykład metodą uśredniania ważonego dotyczyć będzie tych zrekonstruowanych prognoz. Ogólny schemat postępowania w tej metodzie zilustrowano na rys. 14.4. Klucze reprezentują włączenie bądź wyłączenie danego składnika niezależnego z procesu rekonstrukcji.
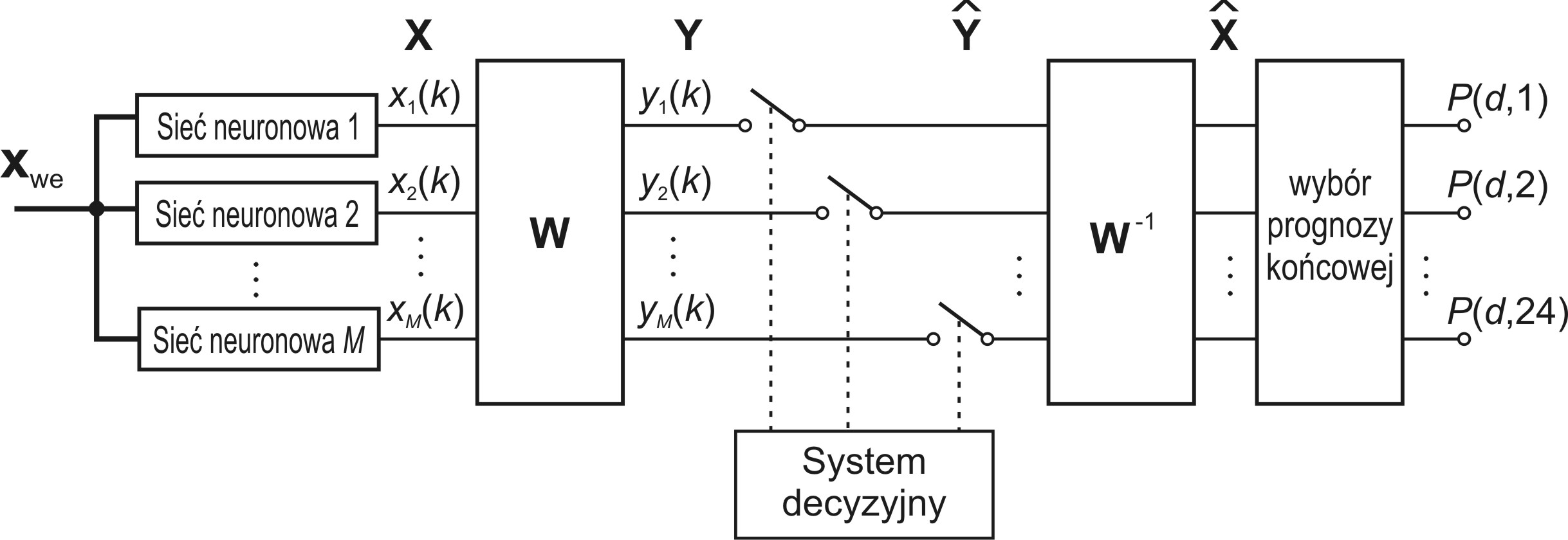
Problemem w tej metodzie pozostaje oczywiście rozpoznanie, które składniki niezależne należy traktować jako nieistotne. Niekiedy z obserwacji przebiegu czasowego składników niezależnych można z dużą dozą prawdopodobieństwa rozpoznać powtarzalne wzorce odpowiadające składnikom istotnym rozkładu. Najlepszym sposobem potwierdzenia tego jest określenie macierzy autokorelacji odpowiadającej każdemu z tych składników. Szum jest zwykle nieskorelowany (bądź słabo skorelowany), co przejawia się poziomem współczynnika korelacji bliskim zeru dla opóźnień różnych od zera.
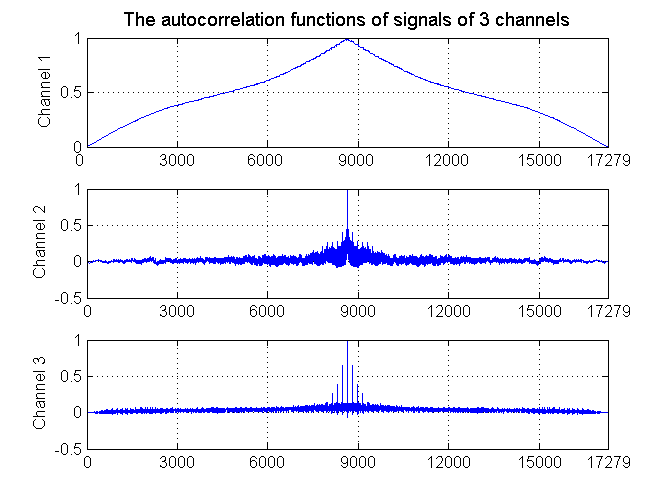
Sytuację taką przy trzech składnikach niezależnych dla kolejnych opóźnień odpowiadających 8600 godzinom (dla PSE) w roku przedstawiono na rys. 14.5. Składnik pierwszy reprezentuje najważniejszy sygnał użyteczny. Składnik drugi odpowiada typowemu szumowi natomiast w składniku trzecim poza szumem można również wyodrębnić również niewielką zawartość istotnej informacji.
14.3.3 Integracja przy użyciu sieci neuronowej
Innym sposobem integracji wyników wielu predyktorów jest zastosowanie jako integratora dodatkowej sieci neuronowej. W metodzie tej wektory 24-elementowe wygenerowane przez poszczególne predyktory łączone są w jeden wektor wejściowy \( \mathbf{z}=\left[\begin{array}{llll} \mathbf{x}_1^T, & \mathbf{x}_2^T, & \ldots, & \mathbf{x}_M^T \end{array}\right]^T \). Przy M predyktorach wymiar takiego wektora jest równy 24M. Pierwszym krokiem tej procedury musi być redukcja wymiaru takiego wektora. Jest ona dokonywana poprzez dekompozycję PCA [46], stanowiącą transformację liniową \(\mathbf{y}=\mathbf{Az}\), w której macierz \( \mathbf{A} \subset R^{K \times 24 M} \) jest tworzona na podstawie najważniejszych wektorów własnych macierzy autokowariancji odpowiadającej wektorom z. W wyniku tej dekompozycji wektor y zawiera jedynie wybraną przez użytkownika liczbę \(K\) składników głównych, które stanowić będą sygnały wejściowe dla sieci neuronowej stanowiącej integrator. Może nim być dowolna sieć neuronowa z nauczycielem (np. MLP lub SVM). Schemat integracji przy wykorzystaniu tej metody przedstawiony jest na rys. 14.6 [48].
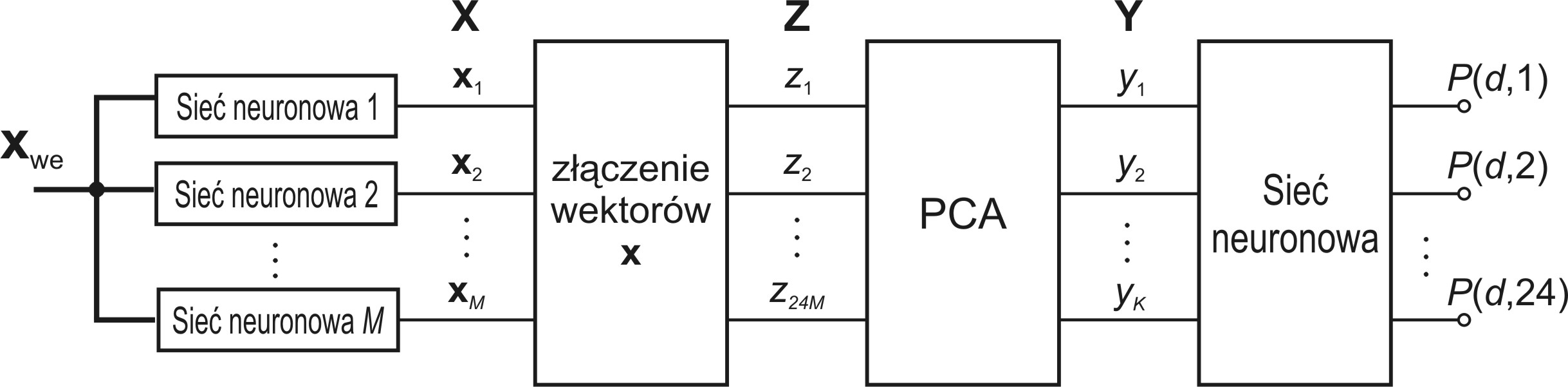
W wyniku badań stwierdzono, że zarówno sieć MLP jak i SVM dobrze sprawdzają się w roli integratora ze względu na efektywny algorytm uczący i dobrą skuteczność tego typu sieci, znacznie przewyższającą pozostałe rozwiązania.
14.3.4 Integracja dynamiczna zespołu
Integracja dynamiczna zespołu zakłada zasadniczo inną filozofię działania [47]. W zespole składającym się z \(M\) predyktorów wybiera się ten, który najlepiej sprawdził się na uczących danych wejściowych \(\mathbf{x}_l\) najbliższych danym testującym \(\mathbf{x}_t\) i on generuje ostateczną prognozę zespołu. Bliskość wektorów określa się przy pomocy wybranej przez użytkownika metryki, na przykład L1, czy L2, obliczając normę różnicy wektorów, najczęściej L1
| \( d\left(\mathbf{x}_t, \mathbf{x}_l\right)=\left\|\mathbf{x}_t-\mathbf{x}_l\right\|_1 \) | (14.12) |
Predyktor który zapewniał najmniejszą wartość błędu prognozy w procesie uczenia dla tego wektora \(\mathbf{x}_l\) jest wybierany z grona \(M\) indywidualnych rozwiązań do wykonania ostatecznej prognozy przy wektorze testowym \(\mathbf{x}_t\). W efekcie takiego rozwiązania dla każdego wektora testowego \(\mathbf{x}_t\) wybór ostatecznego predyktora może być różny. W przypadku wyników uczenia dla wektora \(\mathbf{x}_l\) które są bliskie sobie dla kilku rodzajów predyktorów można zastosować większą liczbę predyktorów i połączyć ich wyniki na wektorze \(\mathbf{x}_t\) metodą uśredniania.