Podręcznik

W tym punkcie przedstawimy wybrane wyniki eksperymentów przeprowadzone dla danych pochodzących z bazy Polskich Sieci Elektroenergetycznych z trzech lat (ponad 26280 godzin). Pierwsze dwa lata zostały użyte w uczeniu wszystkich sieci, natomiast dane z roku trzeciego posłużyły jedynie testowaniu poszczególnych rozwiązań. W rozwiązaniu zastosowano cztery rodzaje rozwiązań: MLP, Elmana, SVM do regresji oraz sieć Kohonena.

W pierwszym etapie badań konieczne jest zaprojektowanie oraz wytrenowanie indywidualnych predyktorów neuronowych. W przypadku sieci sigmoidalnej MLP w wyniku wielu eksperymentów za optymalną uznano strukturę 23-20-19-24 wytrenowaną przy użyciu algorytmu gradientów sprzężonych. Sygnałami wejściowymi dla tej sieci były znormalizowane wartości obciążeń z ostatnich 4 godzin dnia aktualnego oraz 5 godzin (godzina aktualna plus 4 godziny wstecz) z 3 dni poprzedzających prognozę (w sumie 19 składników). Typ dnia zakodowano w postaci 2 bitów (11 – dni robocze, 10 – soboty, 01 – piątki, 00 – święta) podobnie jak porę roku (00 – wiosna, 01 - lato, 10 – jesień, 11 – zima). Każdy neuron wyjściowy reprezentował prognozowane obciążenie o określonej godzinie doby. Ze względu na rozbudowaną strukturę sieci w uczeniu zastosowano metodę gradientów sprzężonych.

Sieć Elmana miała identyczną warstwę wejściową i wyjściową jak MLP. Liczba neuronów ukrytych została ustalona na 8, stąd struktura tej sieci może być zapisana w postaci 23-8-24. W uczeniu tej sieci wykorzystano algorytm Levenberga-Marquardta.

Sygnały wejściowe dla sieci SVM były identyczne jak dla sieci MLP (23 węzły wejściowe). Ze względu na specyfikę sieci SVM należało zastosować równolegle 24 sieci, każda wytrenowana do predykcji obciążenia na określoną godzinę doby. W uczeniu zastosowano zmodyfikowany algorytm programowania sekwencyjnego [51], zaimplementowany na platformie Matlaba [43]. Liczba funkcji jądra (odpowiednik liczby neuronów ukrytych) była każdorazowo dobierana automatycznie przez algorytm uczący przy poziomie wartości tolerancji ε=0.01.

W przypadku zastosowania sieci Kohonena zastosowano 100 neuronów trenowanych za pośrednictwem algorytmu gazu neuronowego na zbiorze uczącym utworzonym z profili zgodnie ze wzorem (14.2). Po wytrenowaniu i zamrożeniu wag nastąpiła analiza sieci, przypisująca zwycięzcę każdemu profilowi wektorowemu dnia. Wyniki testowania były zapisywane w bazie danych. Na etapie rzeczywistego prognozowania wektora profilowego obciążenia na dzień następny odczytuje się z tej bazy zwycięzców odpowiadających temu typowi dnia (np. czwartki miesiąca lipca) i na tej podstawie estymuje się wektor profilowy według wzoru (14.4). Wartości średnie obciążenia prognozowanego dnia i odchylenia standardowe otrzymano z sieci MLP wytrenowanej do tego celu. W przypadku predykcji wartości średnich zastosowano sieć MLP o strukturze 10-6-1 a w przypadku odchylenia standardowego 14-8-1.

Wyniki prognozy dla poszczególnych godzin były porównywane z wartościami rzeczywistymi dotyczącymi danych historycznych. Przy oznaczeniu przez  $P(h)$ i $\hat{P}(h)$ obciążenia odpowiednio rzeczywistego i estymowanego w godzinie h zdefiniowano następujące rodzaje błędów [65].

• Średni względny błąd procentowy (MAPE)

• Błąd średni predykcji (MSE)

• Znormalizowany błąd średni predykcji (NMSE)

gdzie $mean(P)$ jest wartością średnią rzeczywistych obciążeń godzinnych podlegających predykcji.

• Maksymalny błąd średni procentowy (MAXPE)

Powyższe błędy są określane zarówno dla danych uczących jak I weryfikujących (testujących) nie uczestniczących w procesie uczenia. W dalszej części pracy ograniczymy się wyłącznie do błędów testowania na danych nie uczestniczących w uczeniu. Tabela 14.5 przedstawia wartości zdefiniowanych wyżej rodzajów błędów prognozy dla 365 dni roku nie uczestniczącego w uczeniu dla czterech rodzajów sieci zastosowanych jako predyktory (MP – sieć perceptronowa, SVM – sieć SVM, Elman – sieć Elmana, SO – sieć Kohonena).

Tabela 14.5. Błędy predykcji obciążeń w PSE dla danych z jednego roku nie uczestniczących w uczeniu dla 4 indywidualnych predyktorów neuronowych

Wyniki wskazują na sieć MLP jako najlepszy predyktor. Dotyczy to wszystkich kategorii błędów. Następnie wyniki indywidualnych predyktorów zostały zintegrowane przy użyciu 2 różnych metod integracji: BSS oraz sieci neuronowej. Wyniki integracji w postaci zestawienia poszczególnych rodzajów błędów są przedstawione w tabeli 14.6. W przypadku integracji neuronowej zbadano zastosowanie dwu rodzajów sieci: SVM oraz MLP. W przypadku zastosowania BSS do odtworzenia prognozy końcowej zastosowano jedynie 2 składniki niezależne wyselekcjonowane metoda prób i błędów z 4 występujących w rozkładzie.

Tabela 14.6. Błędy predykcji obciążeń w PSE dla zespołu predyktorów neuronowych dla danych z roku nie uczestniczących w uczeniu

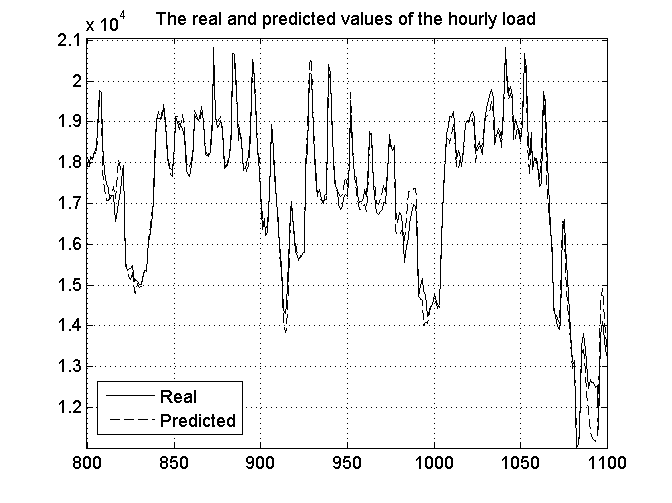
Uzyskane wyniki wskazują na bardzo wysoką sprawność zespołu predyktorów w stosunku do pojedynczej sieci. Porównując poszczególne rodzaje błędów uzyskane przy użyciu najlepszej metody integracji (integracja neuronowa pry użyciu SVM) w stosunku do najlepszej sieci indywidualnej (MLP) uzyskano redukcję błędu MAPE o 28%, MSE o 46% i MAXPE o 36%. Na rys. 14.7 przedstawiono wykresy przewidywanych i rzeczywistych obciążeń godzinnych dla 1100 godzin w roku na danych nie uczestniczących w uczeniu (linia ciągła – dane rzeczywiste, linia przerywana – wielkości prognozowane). Widać bardzo dobra zgodność prognozy z wartościami rzeczywistymi.

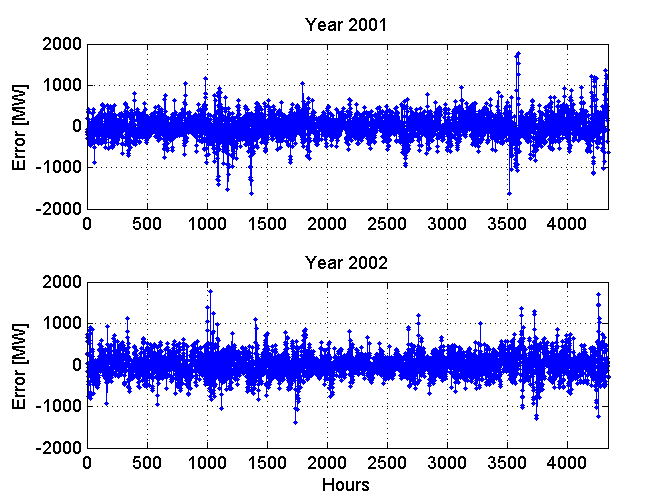
Rys. 14.8 przedstawia rozkład błędów prognozy dla 4300 godzin poddanych prognozie (dane te nie uczestniczyły w uczeniu sieci). Dotyczą one historii obciążeń PSE z dwu różnych lat (2006 i 2007). Charakterystyczny jest zbliżony do siebie poziom błędów prognozy dla poszczególnych godzin. Tylko w niewielkiej ilości godzin błąd ten odstaje od wartości średnich.

Wyniki badań symulacyjnych na danych rzeczywistych z PSE pokazały, że obie metody integracji (BSS lub sieć neuronowa) dobrze sprawują się w praktyce, choć nieco lepsze wyniki uzyskano przy użyciu nieliniowego integratora neuronowego w postaci sieci SVM. Przy zastosowaniu tej techniki uzyskano redukcję błędu MAPE o prawie 30%, błędu MSE o prawie 50% i maksymalnego błędu procentowego MAXPE o ponad 35%. Nie oznacza to jednak wcale, że przy innych zadaniach prognostycznych integracja neuronowa zawsze będzie lepsza niż przy zastosowaniu BSS.