Podręcznik

1. Zespoły klasyfikatorów

1.1. Struktura zespołu i metody integracji

Najbardziej oczywisty i najprostszy wybór werdyktu końcowego zespołu klasyfikatorów to zastosowanie głosowania większościowego (ang. majority voting). Każdy wzorzec charakteryzowany przez odpowiedni zestaw cech podawany jest na wszystkie klasyfikatory i podlega niezależnej klasyfikacji, będąc przypisany do odpowiedniej klasy. Następnie zliczana jest liczba przypisań tego wektora do każdej klasy. Zwycięża klasa, która uzyska największą liczbę wskazań. Jedną z odmian tego trybu jest przyjęcie założenia, że zwycięzca musi uzyskać minimum 50% plus jeden głos. W przeciwnym przypadku przyjmuje się brak rozstrzygnięcia.

Rys. 11.1 Przykładowa struktura zespołu klasyfikatorów.

Jeśli przyjąć identyczne prawdopodobieństwo $\rho$ prawidłowego wskazania klasy przez wszystkie niezależnie działające klasyfikatory i założyć ich nieparzystą liczbę $M$ to zostało udowodnione, że w głosowaniu większościowym statystyczna dokładność zespołu może być wyrażona wzorem [36]

$Acc=\sum_{m=[M / 2]+1}^M\left(\begin{array}{c} M \\ m \end{array}\right) p^m(1-p)^{M-m}$

(11.1)

W tabeli 11.1 przedstawiono wartości dokładności wskazań zespołu przy założeniu różnych wartości prawdopodobieństwa p (identycznego dla każdego klasyfikatora) dla liczby klasyfikatorów tworzących zespół, równej odpowiednio 3, 5, 7 oraz 9. Przyjmuje się pełną niezależność działania klasyfikatorów.

Tabela 11.1 Wartości dokładności Acc wskazania klasy przez zespół M niezależnych, jednakowej jakości klasyfikatorów

	M=3	M=5	M=7	M=9
p=0.6	0.648	0.683	0.710	0.733
p=0.7	0.784	0.837	0.874	0.901
p=0.8	0.896	0.942	0.967	0.980
p=0.9	0.972	0.991	0.997	0.999

Zostało udowodnione teoretycznie, że jeśli wartość $p > 0,5$ to przy liczbie członków zespołu dążącej do nieskończoności dokładność wskazania klasy przez zespół dąży do 100%. Jeśli natomiast $p < 0,5$ to zwiększanie liczby członków zespołu zmniejsza dokładność. Przy $M \rightarrow \infty$ dokładność zespołu zmaleje do zera. Dla $p = 0,5$ zastosowanie zespołu nie zmienia dokładności rozpoznania klasy.

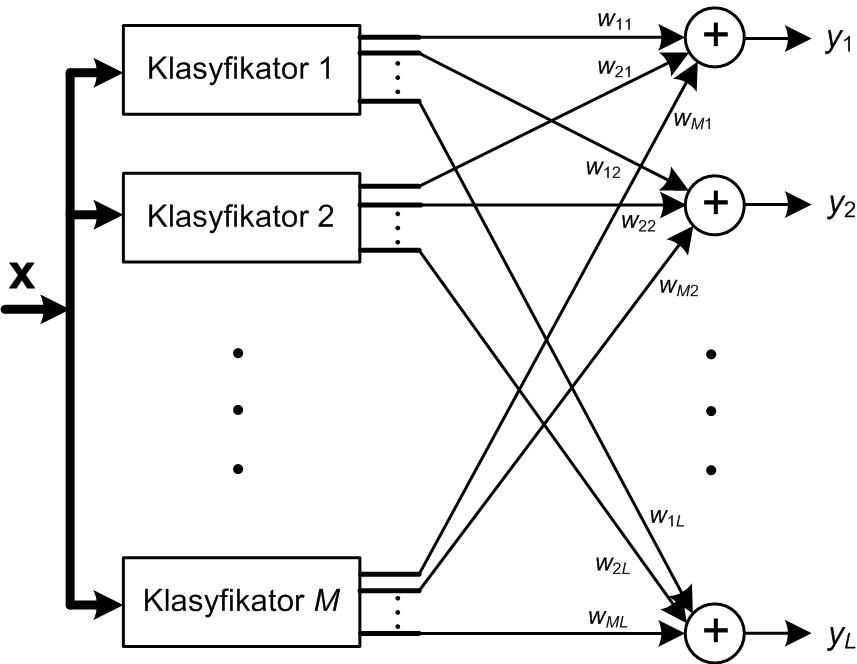
W praktyce rzadko można uzyskać identyczną dokładność wszystkich klasyfikatorów. Eksperymenty numeryczne pokazały, że w takim przypadku głosowanie większościowe nie zawsze gwarantuje uzyskanie wyniku zespołu lepszego niż najlepszy wynik indywidualny. W przypadku nierównej jakości poszczególnych klasyfikatorów można stosować głosowanie większościowe ważone. W tym rozwiązaniu siła głosu klasyfikatora indywidualnego zależy od jego dokładności rozpoznania poszczególnych klas, zmierzoną dla danych uczących (zakłada się, że dane uczące są reprezentatywne dla rozwiązywanego problemu klasyfikacji). Przy M klasyfikatorach tworzących zespół określa się wielkość y_i(x) proporcjonalną do prawdopodobieństwa przynależności wektora x do i-tej klasy według wzoru [49]

$y_i(x)=\sum_{k=1}^M w_{k i} z_{k i}(x)$

(11.2)

w którym w_ki jest wagą z jaką k-ty klasyfikator jest uwzględniany przy rozpoznaniu i-tej klasy, natomiast z_ki jest sygnałem wyjściowym k-tego klasyfikatora odpowiedzialnym za rozpoznanie i-tej klasy (sygnał i-tego wyjścia klasyfikatora). Sygnał ten przyjmuje wartość 1 przy rozpoznaniu przez klasyfikator danej klasy bądź zero w przeciwnym przypadku.

Wartości wag w_kimogą być wyznaczane w różny sposób, uwzględniający jakość poszczególnych członków zespołu. Do typowych rozwiązań należy

$w_{k i}=\frac{\eta_{k i}^m}{\sum_{j=1}^M \eta_{k i}^m}$

(11.3)

gdzie $\eta_{k i}^m$ oznacza wskaźnik jakości (np. dokładność, czułość, precyzję) k-tego klasyfikatora przy rozpoznaniu i-tej klasy, m – wykładnik różnicujący wpływ poszczególnych jednostek zespołu na wynik działania zespołu (np. m= 1, 2, 3). Inny wzór wykorzystuje w integracji zespołu funkcje logarytmiczną [36]

$w_{k i}=\lg \left(\frac{\eta_{k i}}{1-\eta_{k i}}\right)$

(11.4)

Integracja zespołu klasyfikatorów (lub regresorów) jest również możliwa przy zastosowaniu dodatkowej sieci neuronowej, na wejścia której podawane są sygnały decyzyjne wszystkich członków zespołu. Sieć integrująca trenowana jest na danych (X, d), gdzie macierz wejściowa X jest utworzona z decyzji poszczególnych klasyfikatorów a wektor d reprezentuje przynależność klasową (bądź wartość zadaną w problemie regresji) poszczególnych obserwacji.

Zupełnie innym podejściem do integracji zespołu jest zastosowanie naiwnej reguły Bayesa [7]. Oznaczmy przez P(D_j) prawdopodobieństwo, że j-ty klasyfikator przypisuje wektor wejściowy x do odpowiedniej klasy i załóżmy niezależność działania klasyfikatorów.

Prawdopodobieństwo wskazania klasy $d_i$ przez zespół $M$ klasyfikatorów jest wówczas równe

$P\left(d_i \mid \mathbf{D}\right)=\frac{P\left(d_i\right) P\left(\mathbf{D} \mid d_i\right)}{P(\mathbf{D})}=\frac{P\left(d_i\right) \prod_{k=1}^M\left(D_k \mid d_i\right)}{P(\mathbf{D})}$

(11.5)

Ponieważ mianownik powyższej zależności nie zależy od klasy d_k prawdopodobieństwo wskazania k-tej klasy przez zespół przy wystąpieniu na wejściu zespołu wektora wejściowego x jest proporcjonalne do wyrażenia z licznika powyższej zależności (założenie naiwnego klasyfikatora Bayesa). Oznaczmy ten współczynnik proporcjonalności przez µ_k(x). Wówczas

$\mu_i(\mathbf{x}) \approx P\left(d_i\right) \prod_{k=1}^M P\left(D_k \mid d_i\right)$

(11.6)

Prawdopodobieństwa występujące w tym wyrażeniu określa się na podstawie macierzy R rozkładu empirycznego klas (macierz pomyłek). Dla każdego klasyfikatora buduje się taką macierz na podstawie jego wyników klasyfikacji dla danych uczących. Przy M klasach jest to macierz M×M. Niech N_k oznacza całkowitą liczbę obserwacji (wektorów x zbioru uczącego ) należących do klasy k. Wówczas prawdopodobieństwo 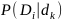może być estymowane w postaci [49]

$P\left(D_k \mid d_i\right)=\prod_{k=1}^M\left(\frac{1}{N_i} R_{i D_k}\right)$

(11.7)

gdzie $R_{i D_k}$ oznacza element macierzy R odpowiadający k-temu wierszowi i D_i-tej kolumnie na którą wskazał i-ty klasyfikator. Przyjmijmy równe prawdopodobieństwo wystąpienia k-tej klasy wśród całej populacji n danych w postaci ułamka

$P\left(d_i\right)=\frac{N_i}{n}$

(11.8)

Wówczas współczynnik proporcjonalności dla wyznaczenia prawdopodobieństwo wskazania i-tej klasy przez zespół może być estymowany w postaci

$\mu_i(x) \approx \frac{1}{N_i^{M-1}} \prod_{k=1}^M R_{i D_k}$

(11.9)

Powyższą procedurę zastosowania metody naiwnej Bayes’a do integracji zespołu klasyfikatorów zilustrujemy na przykładzie hipotetycznego zespołu zawierającego dwa klasyfikatory do rozpoznania 3 klas. Liczba obserwacji uczących jest równa n=30 (każda klasa reprezentowana przez 10 obserwacji). Przyjmijmy, że macierze rozkładu klas dla obu klasyfikatorów są dane w postaci

$\mathbf{R}(1)=\left[\begin{array}{lll} 6 & 2 & 2 \\ 2 & 5 & 3 \\ 1 & 3 & 6 \end{array}\right], \;\;\; \mathbf{R}(2)=\left[\begin{array}{lll} 2 & 4 & 4 \\ 2 & 5 & 3 \\ 4 & 0 & 6 \end{array}\right]$

Każdy wiersz macierzy odpowiada danym należącym do jednej klasy. Kolumna j-ta macierzy wskazuje, ile przypadków zostało przez dany klasyfikator rozpoznanych jako klasa j-ta. Elementy diagonalne odpowiadają danym rozpoznanym właściwie. Element R_ij pokazuje ile razy obserwacja należąca do klasy i-tej została rozpoznana jako klasa j-ta. Dane z obu macierzy wskazują, że N₁=10, N₂=10, N₃=10.

Załóżmy, że testowany wektor x został przypisany przez klasyfikator pierwszy do klasy drugiej, D₁(x)=d₂, a klasyfikator drugi D₂(x)=d₁ wskazał klasę pierwszą jako zwycięzcę. Rozpoznanie ostateczne klasy przez zespół klasyfikatorów będzie zależało od wartości µ_i dla i=1, 2, 3

$\begin{aligned} & \mu_1(\mathbf{x}) \approx \frac{1}{10} \times 2 \times 2=0.4 \\ & \mu_2(\mathbf{x}) \approx \frac{1}{10} \times 5 \times 2=1 \\ & \mu_3(\mathbf{x}) \approx \frac{1}{10} \times 3 \times 4=1.2 \end{aligned}$

(11.10)

Największą wartość osiągnął współczynnik µ₃, stąd decyzją zespołu będzie wskazanie klasy trzeciej jako zwycięskiej dla tej obserwacji x. Zauważmy, że zwyciężyła klasa która nie uzyskała żadnego wskazania klasyfikatorów. To rozwiązanie integracji różni się znacząco od poprzedniej metody, w której zwycięzca był wyłaniany jedynie spośród klas, na którą wskazał co najmniej jeden klasyfikator.