Drukuj ten rozdziałDrukuj ten rozdział

Podręcznik Grafika komputerowa i wizualizacja

Rozdział 3. ELEMENTY GEOMETRII OBLICZENIOWEJ

3.8. Wyznaczenie przecięć w zbiorze odcinków na płaszczyźnie. Metoda zamiatania

Niech dany będzie zbiór odcinków l1, l2 ... ln na płaszczyźnie. Zadanie polega na wyznaczeniu wszystkich przecięć w tym zbiorze. Oczywiście można zaproponować bardzo prosty algorytm, który analizując wszystkie pary (metodą „każdy z każdym”) wyznaczy przecięcia ze złożonością O(n2) . Jednak takie postępowanie nie jest opłacalne, gdyż najczęściej liczba przecięć w takim zbiorze jest dużo mniejsza niż n2.

Zadanie to można rozwiązać stosując tzw. metodę zamiatania. Metoda ta polega na przeglądaniu elementów na płaszczyźnie zgodnie ze wzrostem współrzędnej x („od lewej do prawej”). Do przeglądania wykorzystujemy prostą pionową („miotłę”), która przesuwa się napotykając kolejne elementy. W dowolnym momencie postępowania elementy na płaszczyźnie można podzielić na trzy rozłączne podzbiory (rys.3.16):

  • przetworzone : to elementy, które są po lewej stronie miotły,
  • aktywne : to elementy, które miotła przecina,
  • oczekujące : elementy po prawej stronie miotły.
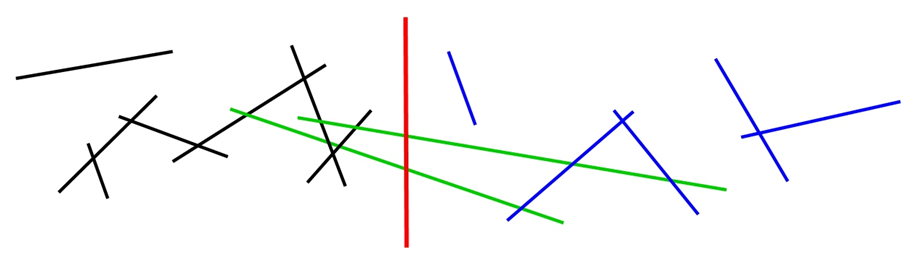
Miotła przechodzi od lewej do prawej w sposób dyskretny: jej kolejne położenia wynikają z położenia charakterystycznych punktów. Aby efektywnie zrealizować „zamiatanie” elementy na płaszczyźnie tworzą tzw. x-strukturę. Jest to struktura zawierająca wszystkie elementy posortowane zgodnie ze wzrostem współrzędnej x charakterystycznego punktu elementów. Dzięki temu „zamiatanie” odbywa się zgodnie z kolejnością elementów w x-strukturze.

Rys.3.16. „Miotła” (czerwona) przesuwana w zbiorze odcinków.
Trzy podzbiory odcinków: przetworzone (czarne), aktywne (zielone), oczekujące (niebieskie).


Aby zastosować metodę zamiatania do wyszukiwania przecięć w zbiorze odcinków na płaszczyźnie należy przyjąć następujące założenia:
  1. Każde dwa odcinki mają co najwyżej jeden punkt wspólny.
  2. Żaden odcinek nie jest pionowy.
  3. Żadna dwa punkty końcowe odcinków nie mają tej samej współrzędnej x.

Założenia te umożliwiają prawidłowe sortowanie zgodnie ze wzrostem współrzędnej x i realizację algorytmu nie wprowadzając zbędnych ograniczeń.

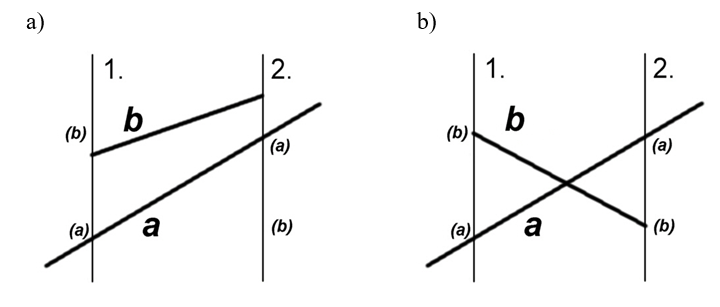
Rys.3.17. Przecięcia „miotły” z odcinkami: 
a) odcinki a i b nie przecinają się:  w 1. i w 2. położeniu „miotła” przecina najpierw a potem b ,
b) odcinki a i b przecinają się: w 1. położeniu „miotła” przecina a, potem b, w 2. najpierw b,  potem a  .


Warto zauważyć, że jeśli rozpatrujemy „miotłę” czyli prostą pionową, która przecina odcinki na płaszczyźnie, to wyszukanie przecinających się odcinków może być wynikiem prostej analizy wzajemnego położenia odcinków i „miotły” (rys.3.17). Rozpatrzmy dwa kolejne położenia „miotły”. Jeśli odcinki a i b nie przecinają się (rys.3.17a), to kolejność (związana ze wzrostem współrzędnej y) przecięć „miotły” z odcinkami jest w obu położeniach taka sama. Natomiast jeśli odcinki a i b przecinają się (rys.3.17b), to kolejność przecięć „miotły” z odcinkami jest różna. A zatem aby sprawdzić czy dwa odcinki przecinają się wystarczy sprawdzić jaka jest kolejność przecięć „miotły” z odcinkami w odpowiednich położeniach. Takie sprawdzenie jest szybsze niż analityczne wyznaczenie przecięcia odcinków (lub stwierdzenie, że nie może ono mieć miejsca).

 

ALGORYTM WYSZUKIWANIA PRZECIĘĆ
1. utwórz x-strukturę-L biorąc pod uwagę mniejszą współrzędną x końców odcinka;
2. utwórz x-strukturę-P biorąc pod uwagę większą współrzędną x końców odcinka;
3. przesuwaj „miotłę” po xi biorąc pod uwagę i x-strukturę-L  i  x-strukturę-P ;
4. if xi należy do x-struktury-L   then
                dodaj do listy aktywnej odcinek, którego koniec określa xi ;
5. if xi należy do x-struktury-P    then
                begin
                            sprawdź, przez analizę przecięć z „miotłą”, czy odcinek, którego
                            koniec określa xi przecina któryś z odcinków listy aktywnej,
                            jeśli tak to wyznacz odpowiednie przecięcie ;
                            usuń z listy aktywnej odcinek, którego koniec określa xi ;
                end

 

Zaprezentowany algorytm wyszukiwania przecięć wykorzystuje efektywnie właściwości stosowania metody zamiatania. Korzystanie z x-struktur i przesuwania „miotły” pozwala ograniczyć sprawdzanie przecięć tylko do grupy odcinków należących do listy aktywnej. Jednocześnie zastosowanie analizy przecięć odcinków z „miotłą” pozwala stwierdzić przecięcie odcinków bez jego wyznaczania. Przedstawiona postać algorytmu jest bardzo ogólna. Nie zawiera między innymi szczegółów operacji na strukturach danych. Złożoność obliczeniowa algorytmu zależy od jego implementacji i sposobu obsługi struktur danych – w analizie przecięć z „miotłą” można wykorzystać odpowiednią y-strukturę odcinków listy aktywnej. Efektywny algorytm wyszukiwania przecięć metodą zamiatania zaproponowali J.L.Bentley i T.A.Ottmann w 1979 roku. Jego asymptotyczna złożoność obliczeniowa wynosi O((s+n)logn) , gdzie s jest liczbą przecięć odcinków. Warto zwrócić uwagę, że gdyby s=n2 (złośliwy przypadek gdy każdy odcinek w zbiorze przecina wszystkie pozostałe) to wyznaczenie przecięć tym algorytmem byłoby znacznie mniej efektywne niż zastosowanie algorytmu naiwnego (analiza każdy z każdym). Jednak w praktyce taki przypadek występuje bardzo rzadko. Najlepszym znanym algorytmem wyszukiwania przecięć odcinków na płaszczyźnie jest algorytm zaproponowany przez I.J.Balabana w 1995 roku. Jego asymptotyczna złożoność obliczeniowa wynosi O(s+nlogn) i jest to algorytm optymalny, gdyż taka złożoność jest dolnym ograniczeniem dla problemu wyszukania wszystkich przecięć odcinków. Natomiast ciekawą właściwością algorytmu I.J.Balabana jest możliwość wyszukiwania przecięć również dla krzywych na płaszczyźnie.

 

Wybrane zagadnienia geometrii obliczeniowej można znaleźć w książce M.Jankowskiego [6], oraz w książkach dotyczących algorytmów i struktur danych [1]. Zainteresowanych tematem odsyłam do książek: M.Berg M. de, Kreveld, M. van, Overmars, O. Schwarzkopf [2] oraz F.P.Preparata i M.I.Shamos [9], które są podstawowymi podręcznikami z tej dziedziny. Dobór i organizacja struktury danych jest ważnym i trudnym problemem w geometrii obliczeniowej; jest także trudnym problemem w grafice komputerowej. Problemowi temu poświęcona jest książka E.Langetepe’a i G.Zachmanna [7]. Książka [10] jest opisem bardzo praktycznych narzędzi geometrycznych (często dość podstawowych) wykorzystywanych w rozwiązywaniu zaawansowanych problemów. Książka [4] zawiera ciekawe rozważania, przede wszystkim, teoretyczne związane ze złożonością obliczeniową różnych wariantów stosowanych algorytmów. Podobne analizy można znaleźć w książce [5], jednak tutaj mamy do czynienia z o wiele bardziej praktycznym podejściem do tematu. Książka ta jest dzisiaj (2024 rok) najprawdopodobniej najobszerniejszym przewodnikiem po narzędziach i algorytmach geometrii obliczeniowej, obejmującym także rzadko spotykane problemy. Warto zwrócić uwagę na fakt, że jest to zbiór kilkudziesięciu obszernych prac (niezależnych artykułów) napisanych przez różnych autorów (zajmuje to ponad 1900 stron). Całość tworzy dość jednorodny podręcznik dzięki trzem redaktorom całości (Goodman J.E. O'Rourke J., Csaba D.T.). Na stronie https://www.csun.edu/~ctoth/Handbook/HDCG3.html jest dostępny pełny tekst (pdf) wstępnej wersji tego podręcznika.