Podręcznik Grafika komputerowa i wizualizacja

Rozdział 4. PRZEKSZTAŁCENIA GEOMETRYCZNE

4.3. Przekształcenia 3D

Możliwe są dwa ustawienia osi trójwymiarowego układu współrzędnych (rys.4.10). Najczęściej do opisu położenia obiektów na scenie (w przestrzeni obiektu) stosowany jest układ prawoskrętny. Natomiast w operacjach związanych z rzutowaniem układ lewoskrętny. Wybór układu współrzędnych dla operacji rzutowania jest konsekwencją naturalnego rozumienia odległości obiektu od obserwatora. Jeśli osie OX i OY zdefiniują układ współrzędnych na rzutni (utożsamianej z płaszczyzną XOY) (pozioma oś OX skierowana w prawo i pionowa oś OY skierowana do góry), to kierunek wzrostu odległości od obserwatora wskaże oś OZ. Tak zdefiniowany układ współrzędnych będzie układem lewoskrętnym.

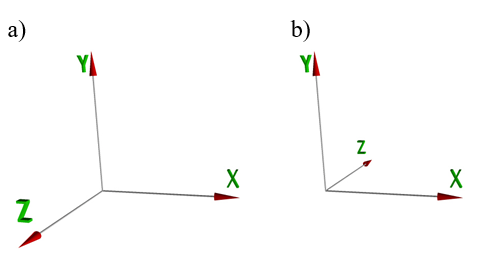
Rys.4.10. Trójwymiarowy układ współrzędnych. a) układ prawoskrętny, b) układ lewoskrętny.
Popatrzmy na układ z punktu (0,0,-d) dla d > 0 .
Jeśli oś OX obrócimy o 90^o zgodnie z ruchem wskazówek zegara
i pokryje się ona wtedy z osią OY, to układ jest prawoskrętny.

Operacje w przestrzeni 3D opisuje macierz 4x4 w przestrzeni 4D. Oczywiście, jeśli wynik mnożenia macierzy jest nieznormalizowany, to należy dokonać normalizacji.

Macierz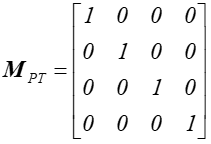

jest macierzą przekształcenia tożsamościowego tzn. takiego, że P' = P . Zmieniając znaki przed współczynnikami (jedynkami) tej macierzy można uzyskać macierze symetrii środkowej względem początku układu współrzędnych, symetrii osiowych względem osi układu współrzędnych i symetrii płaszczyznowych względem płaszczyzn wyznaczonych przez osie układu.

Symetrie osiowe.

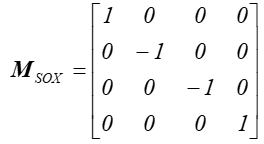
Rys.4.11 Symetria osiowa względem osi OX.

Podobnie macierze opisujące symetrie osiowe względem pozostałych dwóch osi (OY i OZ) mają analogiczną postać ze zmienionymi znakami.

Symetrie płaszczyznowe.

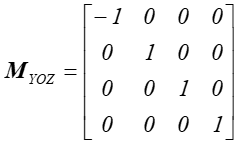
Rys.4.12 Symetria płaszczyznowa względem YOZ.

Macierze opisujące symetrie płaszczyznowe względem pozostałych dwóch płaszczyzn (XOY i YOZ) mają analogiczną postać ze zmienionym znakiem przy 1 w odpowiedniej kolumnie. Warto natomiast zwrócić uwagę na symetrię względem XOY gdyż z punktu widzenia układu współrzędnych przekształcenie to zmienia skrętność układu (rys.4.13).

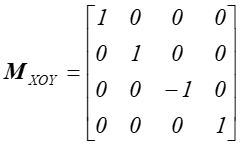
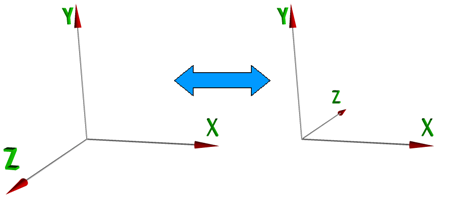
Rys.4.13 Symetria płaszczyznowa względem XOY.
Zmiana skrętności układu współrzędnych.

Symetria środkowa.

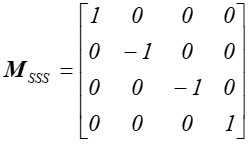
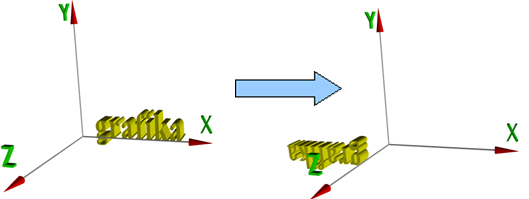
Rys.4.14 Symetria środkowa.

Przesunięcie (translacja).

Rys.4.15 Przesunięcie o wektor T[Tx,Ty,Tz] .

Obroty wokół osi układu współrzędnych.

W układzie współrzędnych kartezjańskich trójwymiarowych zdefiniowanie obrotów wokół osi układu wymaga przyjęcia reguł uznawania obrotów za dodatnie. Najczęściej przyjmuje się konwencję, według której dodatnie obroty są zdefiniowane zgodnie z rysunkiem 4.16.

Rys.4.16. Definicja dodatnich obrotów w prawoskrętnym układzie współrzędnych.

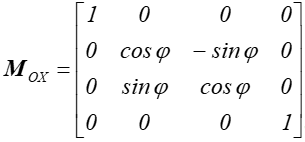
Rys.4.17 Obrót o kąt wokół osi 0X. Obiekt na rysunku został obrócony o kat - 45^o.

Rys.4.18 Obrót o kąt wokół osi 0Y. Obiekt na rysunku został obrócony o kat 45^o.

Rys.4.19 Obrót o kąt wokół osi 0X. Obiekt na rysunku został obrócony o kat 45^o.

Skalowanie.

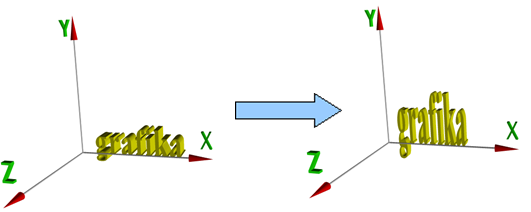
Rys.4.20 Skalowanie obiektu .

gdzie , są współczynnikami skali w odpowiednich osiach.

Skalowanie jest przykładem przekształcenia nieizometrycznego (niezachowującego odległości punktów).

Warto zwrócić uwagę na fakt, że jeśli to skalowanie można opisać macierzą:

wtedy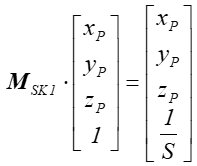

Ale wynik tej operacji nie jest znormalizowany. Zgodnie z przyjętymi wcześniej zasadami posługiwania się współrzędnymi jednorodnymi taka operacja jest w tym przypadku niezbędna.

Zatem co odpowiada skalowaniu ze współczynnikiem S.

Pochylenie 3D.

Rys.4.21 Przykład pochylenia przy zachowaniu kształtu przekroju w płaszczyźnie równoległej do XOY.

Pochylenie jest przykładem przekształcenia nieizometrycznego. Analogicznie można zaproponować przekształcenia i macierze je opisujące dla pochylenia w dwóch pozostałych płaszczyznach.