Podręcznik Grafika komputerowa i wizualizacja

12.5. Całkowanie Monte Carlo

Rozwiązanie analityczne równania renderingu praktycznie nie ma sensu. Autorzy publikacji dotyczących tego tematu czasami sugerują możliwość rozwiązania analitycznego dla wybranego; wydzielonego i wyizolowanego problemu obejmującego na przykład pojedyncze elementy odbijające i jedno źródło światła o prostym opisie geometrycznym. Dla bardziej skomplikowanych scen trudności pojawiają się już na etapie opisu wzajemnego zasłaniania i kształtu jednego elementu widzianego z powierzchni drugiego.

Dobrym rozwiązanie w takiej sytuacji – rozwiązaniem uniwersalnym jest zastosowanie całkowania Monte Carlo. Na przykład dla problemu pojedynczego powierzchniowego źródła światła można wygenerować zbiór promieni biegnących w kierunku odwrotnym od obserwatora do powierzchni i dalej odbijających się zgodnie z pewnym prawdopodobieństwem zależnym od właściwości odbiciowych powierzchni. Promienie odbite trafią (lub nie) w określony punkt powierzchni źródła, z którym to punktem będzie związana określona luminancja i barwa. Jeśli na podstawie analizy zachowania się takich promieni wyznaczymy wartość luminancji postrzeganej przez obserwatora to zadanie jest rozwiązane. Taką właśnie możliwość daje w tym przypadku całkowanie Monte Carlo.

 

W najprostszym przypadku jednowymiarowym, jeśli chcemy obliczyć całkę

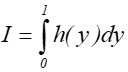
to możemy skorzystać z N liczb losowych o rozkładzie równomiernym   x₁, x₂, ,,,x_N ,   stanowiących pewną realizację zmiennej losowej X. Wtedy

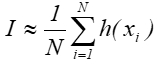
Oczywiście takie proste całkowanie nie byłoby przydatne, gdyż w praktyce problem zachodzi w pewnym przedziale   S   i jednocześnie wymagane jest losowanie próbek o rozkładzie innym niż równomierny.

 

Jak wyznaczyć całkę    ?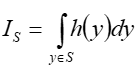

Niech    gdzie     jest gęstością prawdopodobieństwa     .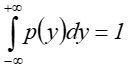

Należy wygenerować N próbek x_i zgodnie z     .

Wartość oczekiwana wyniesie:

               

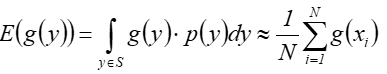
więc

               

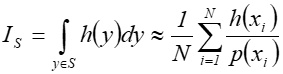
Warto zwrócić uwagę na zależności dotyczące błędu estymacji całki metodą Monte Carlo. Można pokazać, że wariancja estymacji jest proporcjonalna do     natomiast odchylenie standardowe do    .    W związku z tym, jeśli chcemy zmniejszyć błąd o połowę to N musi wzrosnąć czterokrotnie.

 

Generowanie próbek

Zastosowanie całkowania Monte Carlo wymaga wygenerowania próbek o określonym rozkładzie i w zdefiniowanym obszarze. Niestety programy biblioteczne najczęściej pozwalają uzyskać ciąg próbek pseudolosowych o rozkładzie równomiernym w obszarze prostokątnym jednostkowym.

 

Jak wygenerować N próbek x_i zgodnie z,   gdzie jest gęstością prawdopodobieństwa.  .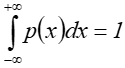

Generowanie wartości losowych zgodnie z zadanym rozkładem gęstości prawdopodobieństwa może być zrealizowane jedną ze znanych metod. Najczęściej stosuje się metodę funkcji odwrotnej do dystrybuanty lub metodę eliminacji próbek niepasujących.

 

Metoda funkcji odwrotnej do dystrybuanty

Metoda ta wymaga analitycznego wyznaczenia dystrybuanty   D(x)   na podstawie funkcji gęstości prawdopodobieństwa, a następnie wyznaczenia funkcji odwrotnej. Uzyskana funkcja przelicza próbki o rozkładzie równomiernym na próbki o zadanym rozkładzie.

    Niech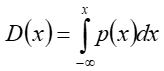   

1. Wygenerować N próbek     o rozkładzie równomiernym,   takich że    .
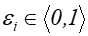2. Wyznaczyć 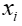   takie że    .  

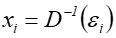  są poszukiwanymi próbkami.

 

Metoda ta jest bardzo efektywna, ale nie zawsze możliwe jest wyznaczenie odpowiedniej funkcji odwrotnej.

Dobrym przykładem wykorzystania metody funkcji odwrotnej do dystrybuanty jest wygenerowanie próbek o rozkładzie równomiernym w kole o zadanym promieniu R.

Wydawać by się mogło, że najprostszym rozwiązaniem takiego zadania będzie wygenerowanie próbek w prostokącie jednostkowym a następnie przeliczenie ich współrzędnych do współrzędnych biegunowych. Takie rozwiązanie nie daje rozkładu równomiernego w kole.

Można to natomiast osiągnąć stosując metodę funkcji odwrotnej do dystrybuanty.

Niech dane będą próbki     o rozkładzie równomiernym, takie że  . 

               

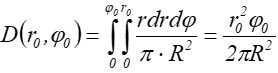
stąd próbki w układzie biegunowym:

                         

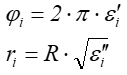
Podane wzory pokazują przeliczenie współrzędnych z układu prostokątnego (gdzie są wygenerowane próbki pseudolosowe o rozkładzie równomiernym w prostokącie jednostkowym) na układ biegunowy koła. Takie przeliczenie zapewnia równomierność rozkładu próbek w kole.

 

Metoda eliminacji próbek (niepasujących)

1. Określić najmniejszy obszar prostokątny obejmujący zadany obszar.
2. Wygenerować próbki o rozkładzie równomiernym w prostokącie.
3. Odrzucić próbki niepasujące – (te, które należą do prostokąta ale nie  należą do zadanego obszaru).

 

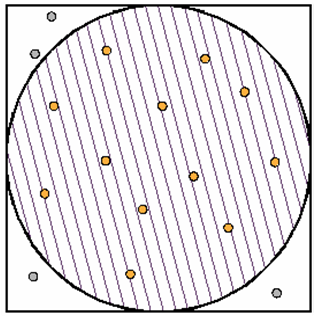
Rys.12.6. Zastosowanie metody usuwania próbek niepasujących do generowania próbek wewnątrz koła.

Metoda ta wymaga zdefiniowania prostokąta obejmującego zadany obszar i wygenerowania próbek o rozkładzie równomiernym. Oczywiście część z nich będzie poza zadanym obszarem – należy je odrzucić. Metoda ta może być praktycznie zawsze zastosowana – nie ma żadnych ograniczeń ani problemów analitycznych. Nie jest ona jednak efektywna, gdyż wymaga generowania dużej liczby próbek, które nie są potem wykorzystywane.

Na rysunek 12.6 pokazano zastosowanie tej metody do generowania próbek w kole, część próbek leżących poza obszarem koła zostaje odrzucona.