Podręcznik Grafika komputerowa i wizualizacja

12.12. Metody przyspieszające śledzenie promieni

Barwa każdego piksela obrazu jest wyznaczana w podobny sposób przez analizę odpowiedniego drzewa przecięć. Liczba operacji z tym związanych rzutuje na czas obliczeń całości. Z drugiej strony można wskazać operacje, które pojawiają się najczęściej – są to z reguły operacje związane z szukaniem przecięcia promienia z powierzchnią obiektu. Stąd algorytmy przyspieszające metodę śledzenia próbują zredukować koszty obliczeń albo przez przyspieszenie wyznaczania przecięć, albo przez zmniejszenie nakładu pracy związanej z analizą drzewa.

 

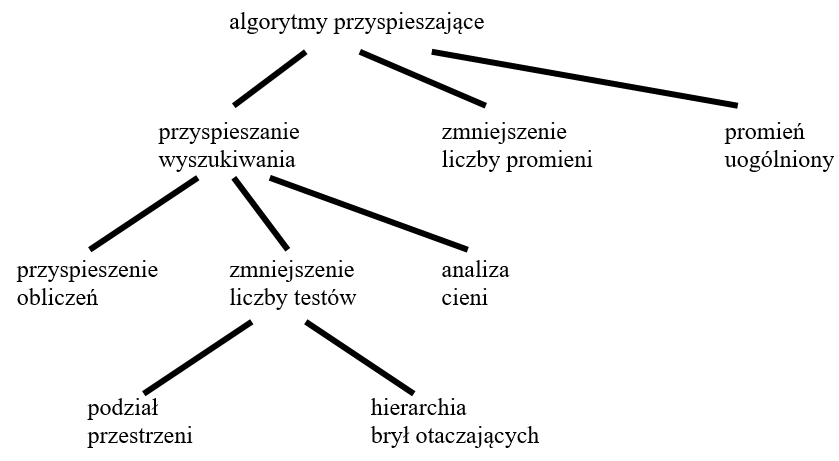
Rys.12.12. Wybrane algorytmy przyspieszania.

 

Zmniejszenie kosztów obliczeń przecięć promieni z powierzchniami

Metody te koncentrują się z jednej strony na operacjach numerycznych, a z drugiej na technice wyboru promieni do analizy.  Stąd najczęściej wymienia się następujące grupy metod:

Stosowane operacje matematyczne i uproszczenia opisu mają na celu wyłącznie zmniejszenie powtarzanych obliczeń. Odbywa się to przez wyznaczenie wartości pewnych wyrażeń (wybierane są takie wyrażenia, których wartości są niezależne od równania promienia) w preprocesingu przed analizą biegu promienia. Wyniki tych obliczeń są później wykorzystywane w trakcie śledzenia promieni. Dzięki temu unika się wielokrotnego powtarzania tych samych operacji matematycznych. Oczywiście możliwość optymalizacji tą drogą wymaga dość żmudnej analizy równań powierzchni, a efektywność przyspieszenia bardzo ściśle zależy od opisu powierzchni. Nie prowadzi to natomiast do przybliżenia ani zmiany wartości obliczeń końcowych.

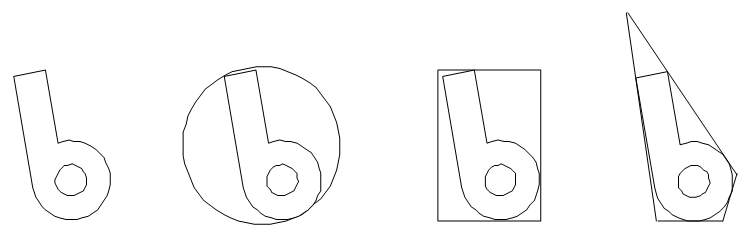
Rys.12.13. Przykłady różnych brył otaczających. Kula daje możliwość
szybszego wyznaczenia przecięcia ale gorzej przylega do obiektu.
Wielościan może ciasno przylegać do obiektu ale trudniej wyznaczyć przecięcie z promieniem.

 

Zmniejszenie liczby testów

Stwierdzenie czy promień przecina dany obiekt jest zadaniem trudnym. Zastosowanie odpowiedniej techniki wyboru promieni, które mają szansę na przecięcie, pozwala wyeliminować zbędne przypadki, dla których nie trzeba przeprowadzać długiej i kosztownej, pełnej analizy biegu promienia.

Techniki wyboru promieni (techniki zmierzające do zmniejszenia liczby testów) można podzielić na dwie grupy: zastosowanie brył otaczających i podział przestrzeni.

Hierarchia brył otaczających

Zanim rozpocznie się wyznaczanie przecięcia promienia z powierzchnią obiektu, można wykorzystując hierarchię brył otaczających spróbować wyznaczyć przecięcie z bryłą otaczającą obiekt. Jeśli promień nie przecina takiej bryły, to analiza przecięcia z obiektem nie jest konieczna. Oczywiście aby w takiej sytuacji można było mówić o przyspieszeniu obliczeń powinny być spełnione dwa warunki. Bryła powinna „ściśle” (ciasno) otaczać obiekt oraz wyznaczenie przecięcia promienia z bryłą powinno być wielokrotnie prostsze (i szybsze) niż przecięcia z obiektem. Często te warunki są sprzeczne. Najczęściej stosuje się kule, wielościany lub „pasy” równoległych płaszczyzn jako bryły otaczające. Kula jest obiektem, dla której najszybciej można stwierdzić, czy jest przecięta prostą czy nie. Wystarczy znaleźć odległość prostej od środka kuli i porównać z promieniem. Jest to szybsze niż sprawdzanie przecięcia prostej z prostopadłościanem. Wadą kuli jako obiektu otaczającego jest najczęściej niezbyt ciasne obejmowanie obiektu. Warto zwrócić uwagę na przecięcia z obiektami typu AABB (ang. Axis-Aligned Bounding Box - prostopadłościan o krawędziach wyznaczonych przez proste równoległe do osi układu współrzędnych) i OBB (ang. Oriented Bounding Box - prostopadłościan dowolnie zorientowany)  Aby zwiększyć efektywność działania metody można skonstruować hierarchię brył otaczających.

Podział przestrzeni

Niejako odwrotne podejście do problemu w stosunku do hierarchii brył otaczających stanowi podział przestrzeni. W tym przypadku całą przestrzeń sceny dzieli się na prostopadłościenne sektory. Następnie zamiast otaczać obiekt przyporządkowuje się mu odpowiedni sektor (sektory), w którym obiekt się znajduje. Dzięki temu analizując drogę promienia przez kolejne fragmenty przestrzeni można sprawnie wybrać obiekty, które w nich się znajdują. Stosuje się podział równomierny lub nierównomierny. W tym drugim przypadku jest podział hierarchiczny: drzewo ósemkowe lub binarne.

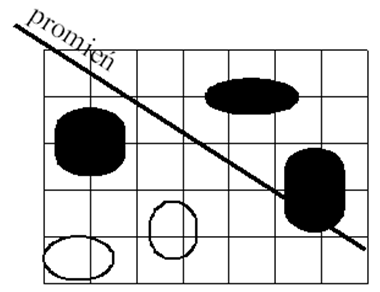
Rys.12.14. Równomierny podział przestrzeni.

Zmniejszenie liczby promieni

Wyróżnia się dwa przypadki. Zmniejszenie liczby promieni pierwotnych i/lub zmniejszenie liczby promieni wtórnych.

W pierwszym przypadku zakłada się, że barwy sąsiednich pikseli są zbliżone. Można więc przeprowadzić dokładne obliczenia dla mniejszej rozdzielczości rastra niż w rzeczywistości (np. dla co czwartego piksela), natomiast pozostałe piksele wyznaczyć dokonując interpolacji. Oczywiście warto zastosować mechanizm adaptacyjny. Przyjąć maksymalną różnicę wartości, która dopuszcza interpolację – przekroczenie jej spowoduje wyznaczenie wartości piksela po przeprowadzeniu dokładnych obliczeń, a nie w wyniku interpolacji.

W drugim przypadku dla każdego piksela zmniejsza się głębokość drzewa kolejnych przecięć lub odbić, dzięki czemu nie są brane pod uwagę kolejne promienie.

Pominięcie niektórych pikseli lub zmniejszenie rozdzielczości rastra oznacza po prostu zmniejszenie dokładności wyznaczenia rozkładu oświetlenia. Podobny problem powstanie w przypadku nadpróbkowania. Jeśli jest ono stosowane, to liczba próbek na piksel wynika z założonej dokładności obliczeń i rezygnacja nawet adaptacyjna z pewnej liczby próbek pogarsza tę dokładność. Przy wykorzystaniu metody adaptacyjnej redukcji promieni pierwotnych w typowych zastosowaniach metody śledzenia często oprócz wspomnianego warunku wartości progowej uwzględnia się kilka innych wymaganych do skorzystania z interpolacji.:

Metoda jest bardzo atrakcyjna obliczeniowo, jednak może pogarszać jakość końcową. Dobór właściwie zastosowanych kryteriów korzystania z interpolacji powinien zapewnić kompromis dający niewidoczne spadki jakości przy zauważalnej redukcji czasu obliczeń.

Zmniejszenie kosztów wyznaczania cieni

Metody te można podzielić na podgrupy:

Metody analizy gęstości zakładają, że jeśli promień trafi, na drodze do źródła światła, w obszar w którym znajduje się odpowiednio duża liczba obiektów („gęstość” powyżej pewnego progu), to zostanie on zatrzymany i do tego źródła nie dotrze. Można tak przyjąć z dużym prawdopodobieństwem, bez analizy przecięć z konkretnymi obiektami z tego obszaru. Takie postępowanie czasami prowadzi do błędów, które wprawdzie nie przeszkadzają w odbiorze filmów czy reklam, ale mogą zafałszować obraz rozkładu oświetlenia. Problemu tego nie stwarzają metody zmniejszające głębokość drzewa promieni wtórnych po znalezieniu obiektu zasłaniającego źródło światła. Przy analizie oświetlenia złożonych elementów, przy dużej liczbie obiektów i jednocześnie dużej liczbie źródeł światła powstaną strefy cienia dające możliwość redukcji obliczeń tą metodą.

Przetwarzanie równoległe

Proces obliczeniowy dla pojedynczego piksela jest praktycznie niezależny od obliczeń związanych z sąsiednimi pikselami. Teoretycznie więc, każdy piksel mógłby być liczony przez niezależny komputer, a potem z gotowych pikseli można byłoby złożyć obraz. W praktyce bardzo rzadko zdarza się możliwość dysponowania tak dużą liczbą jednostek obliczeniowych. Można więc, podzielić obraz na dowolne fragmenty i rozdzielić je pomiędzy jednostki obliczeniowe maszyny równoległej.

Podczas produkcji filmów wykorzystuje się możliwość niezależnego, równoległego wyznaczania całych obrazów, np. kolejnych klatek filmu lub możliwość innego rozłożenia filmu na obrazu lub fragmenty do równoległej obróbki. Wymaga to oczywiście udziału wielu komputerów lub specjalizowanego sprzętu wieloprocesorowego

Promienie uogólnione

Analizowana jest wiązka promieni w postaci stożka lub walca.
Technika ta jest stosunkowo rzadko wykorzystywana. Chociaż analiza wiązek promieni może być zgodna z oczekiwaniem wyznaczenia kierunków, z jakich cały obiekt jest oświetlony przez dane źródło. A zatem teoretycznie byłoby to pomocne np. gdy na scenie znajduje się wiele przedmiotów i oświetlone są one kilkoma źródłami światła. Jednak teoretyczne korzyści metody wiążą się niestety z wieloma problemami pojawiającymi się w praktycznych zastosowaniach.

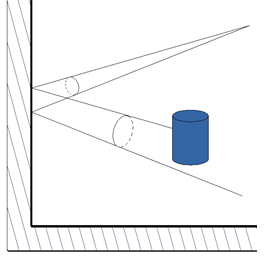
Rys.12.15. Przecięcie promienia uogólnionego z obiektem.