Podręcznik Grafika komputerowa i wizualizacja

11.7. Interpolacja odbicia - cieniowanie

Wyznaczenie barwy związanej z modelem oświetlenia dla każdego punktu/piksela jest zadaniem kosztownym. Można zatem rozpatrywać interpolację, która pozwoli wypełnić barwą wielokąty w sposób uproszczony. Stosuje się trzy warianty takiego wypełnienia – trzy warianty interpolacji (cieniowania).

 

Cieniowanie płaskie jest zgodne z rzeczywistością, gdy obserwator lub źródło światła znajduje się w nieskończoności. Może być także stosowane, gdy wielokąt reprezentuje rzeczywiście powierzchnię modelowaną – mamy wtedy do czynienia z rzeczywistą powierzchnią wielościenną.

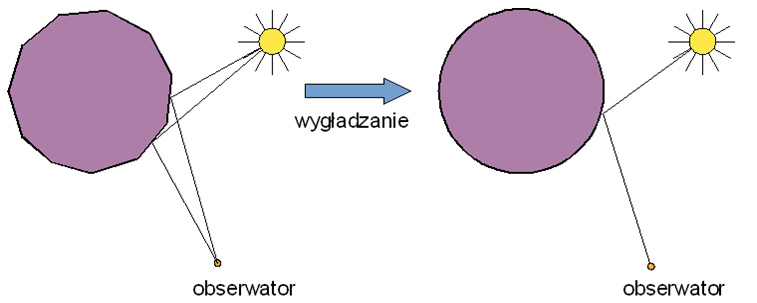
Rys.11.11. Wygładzanie wielościennego obiektu. W praktyce nie ma możliwości zmiany
kształtu powierzchni obiektu. Nie ma zatem możliwości wygładzenia kształtu.
Można jednak ten sam efekt uzyskać zmieniając rozkład barw  na powierzchni.

Jeżeli jednak złożony kształt powierzchni obiektu jest przybliżony wielościanem, to można za pomocą cieniowania wygładzić (pozornie – rysunek 11.11) obiekt niwelując wielościenny charakter.

 

Cieniowanie Gouraud

Cieniowanie Gouraud pozwala wypełnić wielokąty przez liniową interpolację barwy, jest procesem dwuetapowym:

W pierwszym etapie jest wyznaczana (hipotetyczna) barwa w wierzchołkach wielościanu. W tym celu wyznaczamy hipotetyczny wektor normalny jako średnią arytmetyczną wektorów normalnych wszystkich ścian, do których ten wierzchołek należy. Następnie na podstawie wektora normalnego wyznaczamy barwę wierzchołka korzystając z wybranego modelu odbicia światła.

W drugim etapie dokonywana jest liniowa interpolacja barwy zgodnie z zaprezentowanymi wzorami na rysunku 11.12.

 

Rys.11.12. Cieniowanie Gouraud. Poszukujemy barwy w punkcie E.

 

11.6.2 Cieniowanie Phonga

Cieniowanie Phonga polega na analogicznej interpolacji jak w cieniowaniu Gouraud, tylko że interpolowana jest nie barwa ale wektor normalny.

W pierwszym etapie wyznaczamy wektor normalny w wierzchołkach w ten sam sposób jak w cieniowaniu Gouraud.

W drugim etapie wyznaczamy interpolowany wektor normalny dla każdego piksela (to znaczy dla punktu powierzchni odpowiadającego pikselowi) – rysunek 11.13. Następnie wyznaczamy barwę piksela, na podstawie interpolowanego wektora normalnego korzystając z wybranego modelu odbicia światła.

 

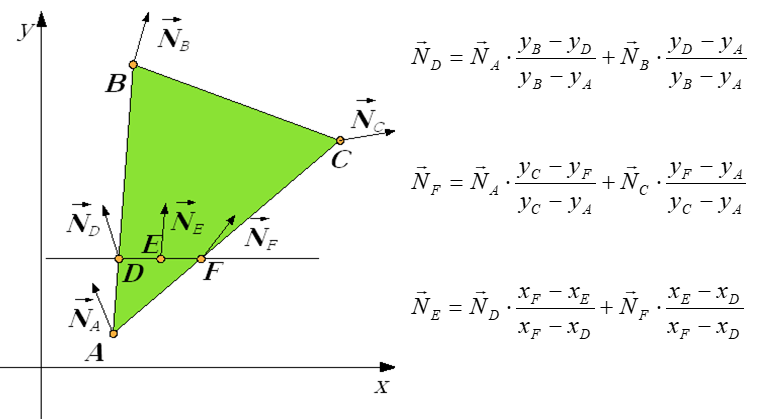
Rys.11.13. Cieniowanie Phonga. Poszukujemy wektora normalnego w punkcie E.
Na jego podstawie wyznaczana jest barwa w punkcie E.

 Cieniowanie – porównanie interpolacji

 Porównując cieniowanie Gouraud i Phonga (rys.11.14) można wskazać właściwości każdego z nich.

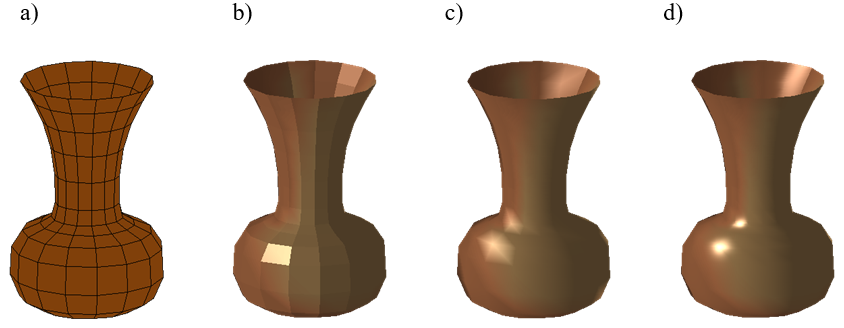
Rys.11.14. a) Model nieoświetlony, b) Cieniowanie płaskie,  c) Cieniowanie Gouraud, d) Cieniowanie Phonga.

 Problemy cieniowania

Obie przedstawione tutaj metody przybliżają rzeczywisty rozkład barw. W specyficznych sytuacjach powoduje to, powstawanie błędów.  Obie metody są wrażliwe na orientację cieniowanego obiektu. Jeśli obiekt ma różne barwy w wierzchołkach i zostanie obrócony, to interpolacja da różne efekty w zależności od położenia obiektu. 

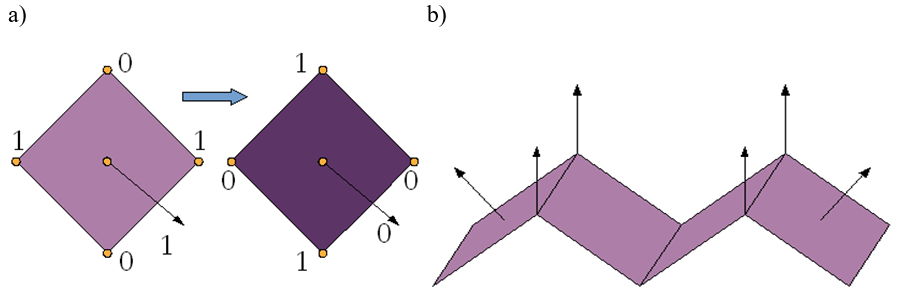
Rys.11.15. Powstawanie błędów cieniowania. a) Obrót obiektu. b) Problem z interpolowanymi wektorami normalnymi.

Rozpatrzmy kwadrat, który ma różne barwy wierzchołków (rysunek 11.15 a). Niech wartości luminancji dla kolejnych wierzchołków wyniosą odpowiednio 0, 1, 0, 1. Jeśli dla takiego kwadratu luminancja środka kwadratu będzie liczona z zastosowaniem interpolacji liniowej, to uzyskana wartość będzie zależała od położenia wierzchołków kwadratu względem kierunku interpolacji. Obrócenie kwadratu zmienia efekt interpolacji – rysunek 11.15 a).

W obu metodach liczy się hipotetyczne wektory normalne w wierzchołku wielościanu na podstawie średniej arytmetycznej wektorów normalnych sąsiadujących ścian. Może to spowodować powstanie błędnie skierowanych wektorów interpolowanych. Na rysunku 11.15 b) wektory interpolowane wewnętrznych ścian będą inaczej skierowane niż rzeczywiste wektory normalne. Dodatkowo powstaje nieoczekiwany wpływ ścian sąsiednich. Ruch jednaj ściany zewnętrznej spowoduje zmianę hipotetycznego wektora normalnego w wierzchołku (przez wpływ na średnią), a w konsekwencji tego zmianę wektora interpolowanego ściany wewnętrznej.