Podręcznik Grafika komputerowa i wizualizacja
Rozdział 5. RZUTOWANIE I WIRTUALNA KAMERA
5.3. Opis macierzowy rzutowania
Rzutowanie może być opisane macierzowo, analogicznie do opisu operacji geometrycznych zaprezentowanych wcześniej.
Rozpatrzmy rzutowanie
perspektywiczne w przestrzeni obserwatora. Współrzędne opisują położenie w
lewoskrętnym układzie współrzędnych obserwatora 0XYZ. Niech obserwator (środek
rzutowania) znajduje się w początku układu współrzędnych, a rzut jest dokonywany
na płaszczyznę z = d dla d>0 (rys.5.5). Rzutem
punktu P o współrzędnych (xp,yp,zp) będzie punkt P' o współrzędnych (x'p,y'p,z'p) , który zgodnie z definicją rzutu perspektywicznego będzie
należał do płaszczyzny rzutni i jednocześnie do prostej przechodzącej przez
środek rzutowania i punkt P .
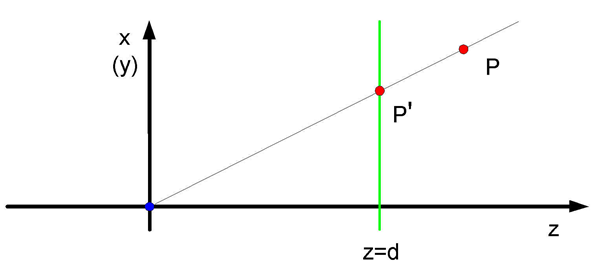
Rys.5.5. Rzut perspektywiczny. Rzutnia o
równaniu z = d ,
środek rzutowania (niebieski punkt) o współrzędnych (0,0,0)
, d>0 .
Uwzględniając proste zależności geometryczne można pokazać, że macierz opisująca tak zdefiniowane rzutowanie perspektywiczne ma postać:
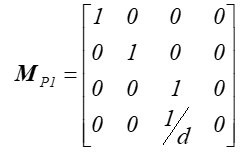
Warto zwrócić uwagę na to, że macierz ta definiuje operację wymagającą normalizacji, bowiem zależność między współrzędnymi punktu i jego rzutu ma postać:
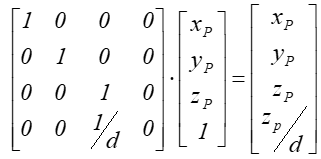 po normalizacji
po normalizacji 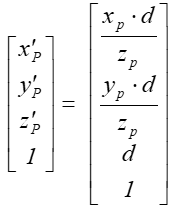
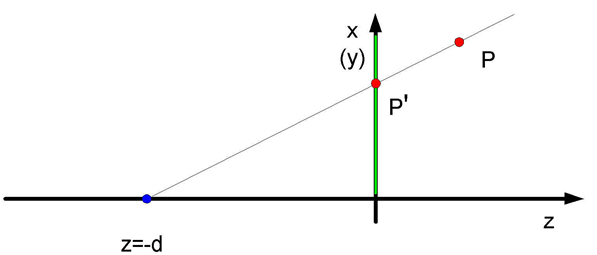
Rys.5.6. Rzut
perspektywiczny (wersja druga). Rzutnia o równaniu z = 0 ,
środek rzutowania (niebieski
punkt) o współrzędnych (0,0,-d) , d>0 .
Rzutowanie perspektywiczne można również prosto zdefiniować w nieco inny sposób (rys. 5.6.). Niech w analogicznym układzie współrzędnych obserwator (środek rzutowania) znajduje się w punkcie (0,0,-d) dla d>0 , a płaszczyzna rzutni ma równanie z = 0 (rys.5.6). Macierz rzutowania będzie wtedy miała postać:
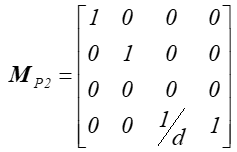
Zaś zależność między współrzędnymi punktu i jego rzutu ma teraz postać.:
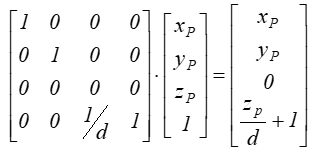 po normalizacji
po normalizacji 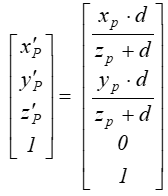
Oba warianty definicji rzutowania perspektywicznego mogą być stosowane zamiennie zależnie od sytuacji.
Jeżeli w drugim
przypadku przyjmiemy, że d →![]() to promienie rzutujące
zamiast pęku prostych utworzą proste równoległe i uzyskamy rzutowanie
równoległe prostokątne (rys.5.7).
to promienie rzutujące
zamiast pęku prostych utworzą proste równoległe i uzyskamy rzutowanie
równoległe prostokątne (rys.5.7).
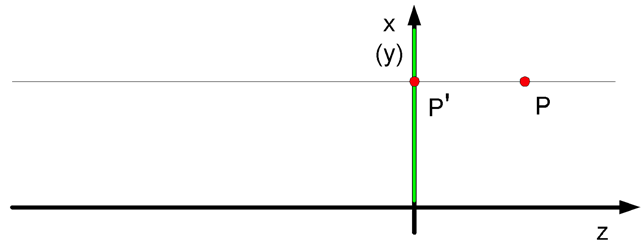
Rys.5.7. Rzut równoległy. Rzutnia o równaniu z = 0 .
O rzutowaniu równoległym można powiedzieć, że jest szczególnym przypadkiem rzutowania perspektywicznego, gdy środek rzutowania znajduje się w nieskończoności. Macierz opisująca ten przypadek będzie miała postać:
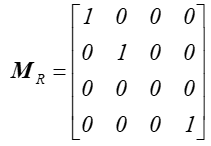
a zależność między współrzędnymi:
g 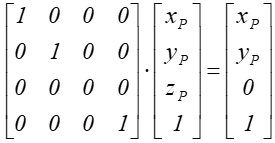 czyli
czyli 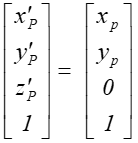
Operacja ta nie wymaga normalizacji.