Podręcznik Grafika komputerowa i wizualizacja

5.4. Ostrosłup widzenia, wirtualna kamera

W dotychczasowych rozważaniach o rzutowaniu nie zwróciliśmy w ogóle uwagi na to, które obiekty (lub ich fragmenty) – które punkty przestrzeni zostaną zrzutowane. A przecież każdy użytkownik aparatu fotograficznego wie, że tylko wybrany przez niego fragment przestrzeni zostanie utrwalony na zdjęciu. To znaczy, że operacje matematyczne wynikające z rzutowania powinny zostać zrealizowane tylko w odniesieniu do określonego zbioru punktów (określonych obiektów). Jeżeli przyjmiemy, że dokonujemy rzutowania perspektywicznego na płaszczyznę i interesuje nas prostokąt obrazu jako część rzutni, to środek rzutowania i prostokąt obrazu wyznaczą pewien fragment przestrzeni, który może zostać „utrwalony”. Jeżeli do tego dodamy dwie płaszczyzny równoległe do rzutni, które ograniczą wybrany fragment z przodu i z tyłu (rys.5.8.), to powstanie figura będąca ostrosłupem ściętym o podstawie prostokątnej nazywana ostrosłupem widzenia lub piramidą widzenia. Zatem po zdefiniowaniu położenia obserwatora (środka rzutowania), rzutni i ostrosłupa widzenia, należy wydzielić te obiekty i punkty przestrzeni, które będą rzutowane. Powstaje problem obcinania w przestrzeni trójwymiarowej. Algorytmy Cohena-Sutherlanda i Cyrusa-Becka można rozszerzyć o możliwość obcinania trójwymiarowego.

 

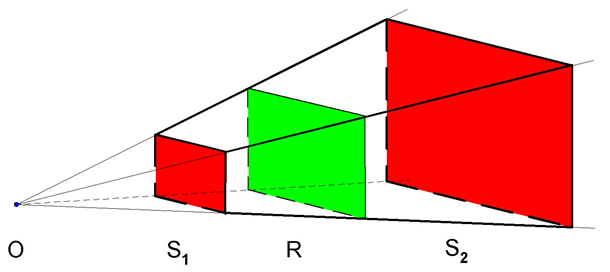
Rys.5.8. Ostrosłup widzenia. R – rzutnia, O – środek rzutowania,
S₁ – przednia płaszczyzna obcinająca, S₂ – tylna płaszczyzna obcinająca.

Dla rzutowania równoległego odpowiednia bryła widzenia zdefiniowana analogicznymi parametrami będzie prostopadłościanem.

      Rzutnia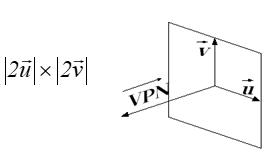 

                                                     

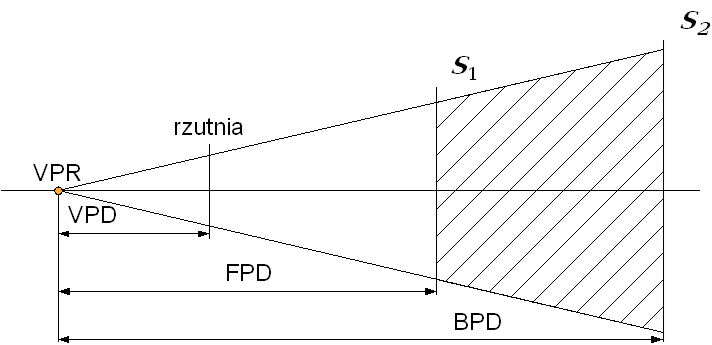
 Rys. 5.9. Opis parametrów rzutu.

Realizacja rzutowania perspektywicznego wymaga definicji parametrów tak, aby jednoznacznie określić bryłę widzenia – rys.5.9. Najczęściej używa się do definicji trójki wektorów  .  Wektordefiniuje oś widzenia (kierunek patrzenia prostopadły do płaszczyzny rzutni). Jednocześnie długość tego wektora określa wysokość ostrosłupa widzenia. Stosowane są dwa podejścia do określenia zwrotu tego wektora. Przyjęty wariant na rysunku powoduje, że kierunek patrzenia wzdłuż osi optycznej jest przeciwny do wektora   . Wektory     definiują płaszczyznę rzutni, a także prostokąt rzutni gdzie będzie powstawał obraz (poprzez długości tych wektorów). Jednocześnie kierunki wektorów określają obrót rzutni wokół osi optycznej. Zestaw wektorów    definiuje jednoznacznie ostrosłup prawidłowy o podstawie prostokąta. Daje to możliwość określenia kąta patrzenia w rzutowaniu perspektywicznym. Komplet parametrów rzutowania wymaga definicji: środka rzutowania (punkt VPR) oraz trzech odległości wzdłuż osi optycznej względem środka rzutowania. Pierwszą jest odległość do płaszczyzny rzutni (VPD). Dwie pozostałe (FPD i BPD) definiują położenie dwóch płaszczyzn (przedniej S₁ i tylnej S₂), które określają ostrosłup ścięty - wyznaczają fragment przestrzeni, która będzie rzutowana.

Patrząc na rzutowanie poprzez analogię do aparatu fotograficznego warto zwrócić uwagę na parametry decydujące o obrazie, który powstanie. Fotograf, wybierając temat do zdjęcia, określa położenie aparatu i kierunek fotografowania. Określa także ogniskową obiektywu (funkcja zoom) czyli kąt „widzenia” aparatu – rys.5.10. Warto przy tym pamiętać, że zdjęcie wykonane obiektywem szerokokątnym z bliskiej odległości jest inne niż obiektywem wąskokątnym (teleobiektywem) z dużej odległości, pomimo pozornego podobieństwa wybranych fragmentów (rys.5.10). Zmiana położenie obserwatora (translacja) powoduje zmiany wzajemnych relacji między punktami obiektu i obserwatorem. Natomiast zmiana ogniskowej obiektywu – kata widzenia (zoom) nie zmienia położenia obserwatora a tym samym nie zmienia wzajemnych relacji między punktami obiektu i obserwatorem. Dobranie właściwego ostrosłupa widzenia jest szczególnie istotne w grach komputerowych i zastosowaniach filmowych grafiki komputerowej.

Rys.5.10. Zdjęcia Gmachu Głównego Politechniki wykonane z różnych miejsc, przy różnych
ostrosłupach widzenia zdefiniowanych za pomocą ogniskowej obiektywu.

Przekładając parametry ruchu aparatu (fotografa) na parametry rzutowania definiujemy wirtualną kamerę. Jaki jest minimalny zestaw operacji,  zapewniający pełną swobodę manipulacji taką kamerą?

Związanie definicji kształtu ostrosłupa widzenia i obrotów z własnym układem współrzędnych wirtualnej kamery zapewnia wygodę manipulacji oraz zgodność symulacji z rzeczywistością.

 Jeśli opisywane dotychczas parametry rzutowania odniesiemy do powstawania obrazu w fotografii, to praktycznie jedynym parametrem aparatu fotograficznego, o którym nie było dotychczas mowy, jest ostrość. Parametr ten nie daje się w prosty sposób przenieść na opis rzutowania. Ostrość zdjęcia jest wynikiem zależności między właściwościami optycznymi obiektywu, a odległością obiektu od obiektywu. Rzutowanie natomiast odwzorowuje wszystkie obiekty w sposób ostry. Niestety, nie jest to zaletą wirtualnej kamery, jeśli obraz ma być zgodny z naszym widzeniem, gdyż akomodacja oka powoduje powstanie widocznych sfer ostrości. Szczególnie jest to niekorzystne w sytuacji wykorzystywania grafiki komputerowej w kinematografii, gdzie nieostrość danego obiektu może być zamierzonym efektem reżysera.

 Rzeczywisty obiektyw aparatu daje ostry obraz punktu w dokładnie określonym miejscu – na płaszczyźnie powstawania obrazu. Zarówno bliżej jak i dalej obrazem punktu jest plamka rozproszenia (rozmyte koło) – stąd nieostry obraz. Analizę zjawiska przeprowadził E. Lommel w końcu XIX wieku. Zaproponował on pewne uproszczenia, stosowane w opisie ostrości do dzisiaj.:

 Pierwsze próby symulacji głębi ostrości na potrzeby grafiki komputerowej zostały podjęte przez M.Potmesila i I.Charkravarty’ego w 1981 roku [3]. Najczęściej stosowanym rozwiązaniem jest dzisiaj sztuczne rozmycie symulujące nieostrość w wybranych fragmentach obrazu. Dokonuje się tego albo stosując bufor akumulacji albo odpowiednie filtrowanie. Więcej na ten temat zainteresowani mogą przeczytać w pracy P.Rokity [4]