Podręcznik Grafika komputerowa i wizualizacja

6.6. Podział przestrzeni

Podział przestrzeni jest sposobem opisu polegającym na rozkładzie obiektu na elementy składowe,  prostsze.

Woksel (voxel) jest najmniejszym elementem przestrzeni 3D (analogicznym do piksela na płaszczyźnie). Wokselowi można przypisać właściwości obiektu/powierzchni:

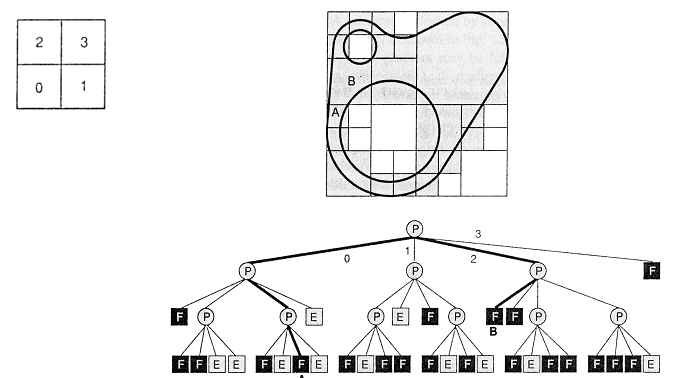
  Rys.6.12. Wskazanie przynależności fragmentów przestrzeni do obiektu   
na płaszczyźnie za pomocą hierarchii 2D :  każdy element w drzewie może być: 
F = full (należy całkowicie),   P = partially full (należy częściowo),
E = empty (nie należy).   Rysunki na podstawie [1].

Można zdefiniować obiekt wskazując, które woksele on zajmuje: reprezentacja przez wskazanie (enumerated representation). Taka reprezentacja jest dekompozycją na komórki, które tworzą regularną siatkę w przestrzeni. Podstawową cechą reprezentacji tego typu jest aproksymacja kształtu z zadaną rozdzielczością. Struktura danych opisująca tak dekomponowaną bryłę będzie listą zajętych komórek.

Podobny efekt można uzyskać strukturą hierarchiczną – drzewem ósemkowym (rys.6.13) wskazując w przestrzeni kolejne prostopadłościenne elementy będące wielokrotnością woksela. W tym przypadku jednak struktura danych (drzewo ósemkowe) da efektywniejszy sposób zapisu (mniejszy koszt pamięciowy). Natomiast aproksymacja kształtu z zadaną rozdzielczością wokselową będzie identyczna. Porównanie różnych podziałów dla tego samego obiektu 2D przedstawiono na rysunku 6.14.

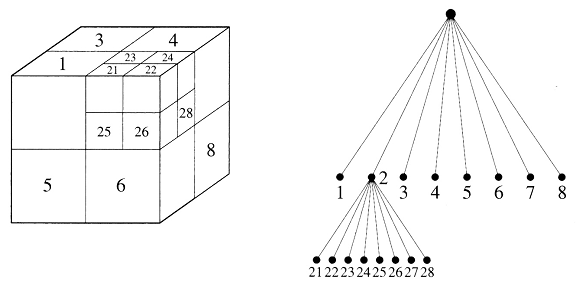
Rys.6.13. Przestrzenne drzewo przynależności:   Hierarchia 3D.

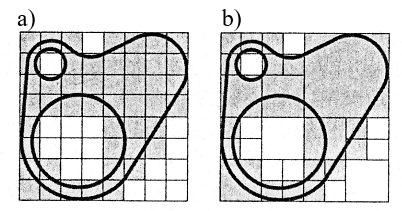
Rys.6.14. Realizacja dwóch różnych podziałów przestrzeni dla tego samego obiektu 2D:
a) podział równomierny (reprezentacja przez wskazanie,
b) hierarchia 2D – drzewo czwórkowe.  Rysunki na podstawie [1].

Alternatywą dla drzewa ósemkowego mogłoby być drzewo podziału binarnego (ang. BSP tree – binary space partitioning tree), w którym  na każdym etapie podziału można wskazać którą półprzestrzeń reprezentuje dany fragment obiektu. Drzewa tego typu nie są jednak stosowane jako samodzielne systemy modelowania. Są natomiast wykorzystywane w algorytmach eliminacji elementów zasłoniętych.

Przechowywanie informacji o budowie obiektu w reprezentacji typu podział przestrzeni prowadzi do problemów zajętości pamięci. Dla podziału N x N x N uzyskujemy złożoność pamięciowa O(N³). Podział 1000x1000x1000  prowadzi do zapamiętania informacji o 1 miliardzie wokseli, a dla każdego może być potrzebna informacja o jego właściwościach.

Warto zwrócić uwagę na aproksymację kształtu obiektu, która zawsze ma miejsce w reprezentacjach realizowanych podziałem przestrzeni (w reprezentacjach wokselowych). Oczywiście błędy aproksymacji maleją ze zmniejszaniem rozmiarów wokseli ale pociąga to za sobą wzrost liczby elementów (lub zwiększanie głębokości drzewa podziału), a tym samym wzrost zajętości pamięci.

Podział przestrzeni daje możliwość stosunkowo prostej realizacji operacji boolowskich. W przypadku reprezentacji przez wskazanie (enumerated representation) należy porównać położenie i zrealizować operację boolowską na poziomie Voxel  –  Voxel. W przypadku hierarchii (drzewa ósemkowego) należy porównać położenie i zrealizować operację na poziomie region  –  region. Warto podkreślić, że podczas realizacji operacji boolowskich dla podziału przestrzeni nie występuje problem regularyzacji.

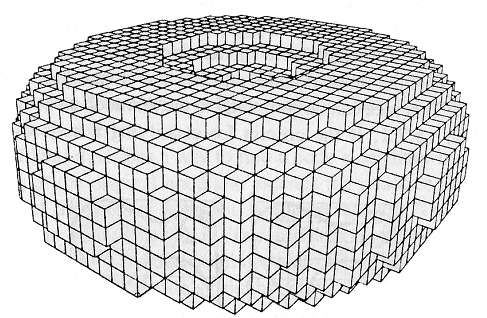
Rys.6.15. Torus reprezentowany przez podział przestrzeni.
Rysunek na podstawie artykułu A.Christensena SIGGRAPH 80.

Podstawowe właściwości podziału przestrzeni można scharakteryzować w następujący sposób.