Podręcznik Grafika komputerowa i wizualizacja

Rozdział 7. MODELOWANIE KRZYWYCH I POWIERZCHNI

7.6. Modelowanie powierzchni

Powierzchnię określa się jako produkt iloczynu tensorowego. Rodzaj powierzchni i jej właściwości będą zależały od tego jaka baza funkcji zostanie wykorzystania.

Jeśli jako funkcje bazowe przyjmiemy wielomiany Bernsteina, to otrzymamy powierzchnie Béziera.

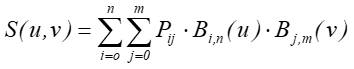
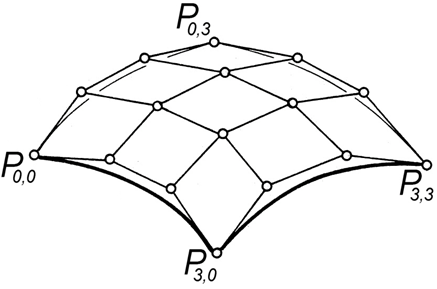
Rys.7.10. Siatka punktów kontrolnych opisująca powierzchnię Beziera. Rysunek na podstawie [1].

Jeśli jako funkcje bazowe przyjmiemy funkcje sklejane, to otrzymamy powierzchnie B-sklejane.

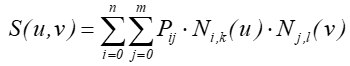
Właściwości powierzchni są analogiczne do właściwości krzywych konstruowanych z wykorzystaniem tych samych funkcji bazowych. Z drugiej strony przyjmując stałość jednego parametru (u lub v) otrzymujemy krzywą (rodzinę krzywych dla różnych wartości parametru

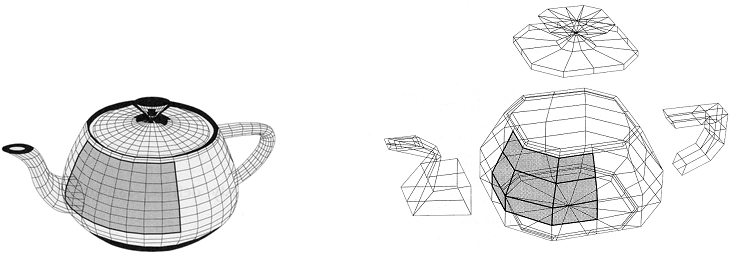
Rys.7.11. Czajnik z Utah i siatka punktów kontrolnych. Obiekt jest modelowany jako zbiór 32 płatów Béziera.
Kształt przykładowego ciemniejszego fragmentu (płata) jest kontrolowany
przez zaznaczony fragment siatki węzłów. Na podstawie [7].

Podczas modelowania powierzchni warto zwrócić uwagę na zalety możliwości lokalnej kontroli kształtu. Zarówno przy wykorzystaniu powierzchni B-sklejanych (gdzie lokalna kontrola jest jedną z podstawowych cech reprezentacji), jak i przy składaniu powierzchni całego obiektu z płatów (np. Beziera jak na rys.7.11).