Drukuj ten rozdziałDrukuj ten rozdział

Podręcznik Grafika komputerowa i wizualizacja

Rozdział 7. MODELOWANIE KRZYWYCH I POWIERZCHNI

7.4. Krzywe Béziera

Krzywe Béziera są zdefiniowane w bazie wielomianów Bernsteina. Ich właściwości mają decydujący wpływ na właściwości krzywych.

Wielomiany Bernsteina są zdefiniowane w następujący sposób:

 

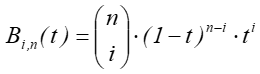                            dla      

 

Podstawowe właściwości:

                       

   

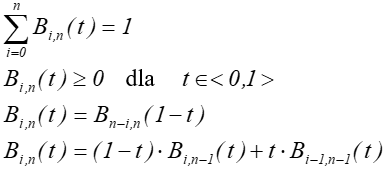
Rys. 7.4. Wykresy wielomianów Bernsteina 2, 3, 4 i 5 stopnia.

 

Ostatnia właściwość (zależność rekurencyjna) prowadzi do algorytmu wyznaczania punktów na krzywej bazującej na wielomianach Bernsteina.

 Najczęściej mamy do czynienia z wielomianami stopnia 3. W tym przypadku:

 

 

Krzywą Béziera opisuje następujące równanie parametryczne:                     
                        punkty Beziera 

 

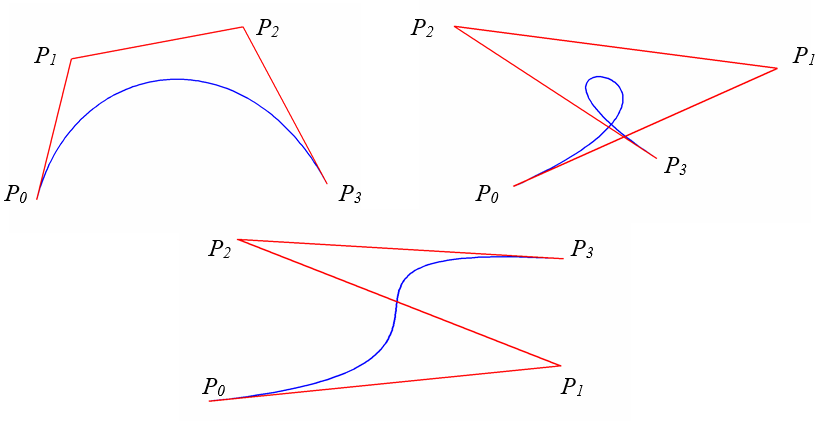
 Rys. 7.5. Przykłady krzywych Béziera

 

Krzywa Béziera zawdzięcza swą nazwę Pierre’owi Bézierowi, warto jednak pamiętać, że rozwiązanie to miało dwóch niezależnych twórców. Drugim był P. de Casteljau. Jego nazwiskiem został opatrzony podstawowy algorytm wyznaczania punktu krzywej.

Krzywa Béziera stopnia n jest definiowana przez n+1 punktów P0, P1, P2,…Pn  w bazie wielomianów Bernsteina. Jest to krzywa gładka, której kształt zależy od położenia punktów kontrolnych. Najczęściej stosowane są krzywe stopnia 3. Użytkownicy komputerów spotykają się z nimi na co dzień w postaci fontów, których kształt jest najczęściej projektowany właśnie z  wykorzystaniem krzywych Béziera stopnia 3.


Właściwości krzywych Béziera

  • Końcowe wierzchołki łamanej P0 i Pn są jednocześnie końcowymi punktami krzywej.
  • Odcinki łamanej 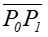  i 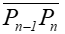  są styczne do krzywej.

  • Krzywa Béziera zawiera się całkowicie w wielościanie wypukłym (wypukłej skorupce), którego wierzchołkami są wierzchołki łamanej.

  • Zmiana numeracji wierzchołków łamanej (od n do 0 zamiast od 0 do n) nie spowoduje zmiany kształtu krzywej.

 Krzywa Béziera interpoluje dwa końcowe punkty kontrolne i aproksymuje pozostałe. Oznacza to, że dla krzywej stopnia 3 , jeśli ustalone są punkty końcowe (a tak jest najczęściej), to dwa pozostałe punkty decydują o kształcie.

Wady krzywych Béziera

  • Brak możliwości reprezentacji krzywych stożkowych.
  • Zmiana reprezentacji krzywej po rzutowaniu perspektywicznym.

Korzystając z właściwości rekurencyjnej wielomianów Bernsteina można wyznaczyć punkty krzywej Béziera algorytmem de Casteljau

 

Algorytm de Casteljau (rys. 7.6)

Wyznaczanie punktu leżącego na krzywej Béziera na podstawie ciągu punktów kontrolnych P0, P1, P2,…Pn

 

    for i:= 0 to n do Pi,0 = Pi;

    for j:=1 to n do

                for i:=j to n  do

                            Pi,j := (1-t).Pi-1,j-1 + t.Pi,j-1;

 

Rys. 7.6. Algorytm de Casteljau. Wyznaczanie punktu leżącego na krzywej Béziera


Jeśli zadaniem jest wyznaczenie dużej liczby punktów leżących na krzywej Béziera to tańszym obliczeniowo rozwiązaniem będzie przejście w wielomianach Bernsteina do postaci naturalnej wielomianu i obliczanie jego wartości algorytmem Hornera.

Łączenie krzywych Béziera

Łączenie segmentów krzywej wymaga zwrócenia uwagi na problem ciągłości. Można wyróżnić różne rodzaje ciągłości łączenia segmentów oraz kryteria z tym związane:

  • Ciągłość geometryczna:   definiowana na podstawie właściwości kierunku (tylko !) wektora stycznego :

    •   G0: początek jednego segmentu końcem drugiego,

    •    G1: zgodne kierunki wektorów stycznych.

  • Ciągłość parametryczna:     definiowana na podstawie ciągłości pochodnej odpowiedniego rzędu.     (Cn – pochodna rzędu n). W praktyce najczęściej:

    •   C0: początek jednego segmentu końcem drugiego,

    •   C1: („prędkość”) zgodne kierunki wektorów stycznych,

    •   C2: („przyspieszenie”) zgodność kierunków i długości wektorów stycznych.


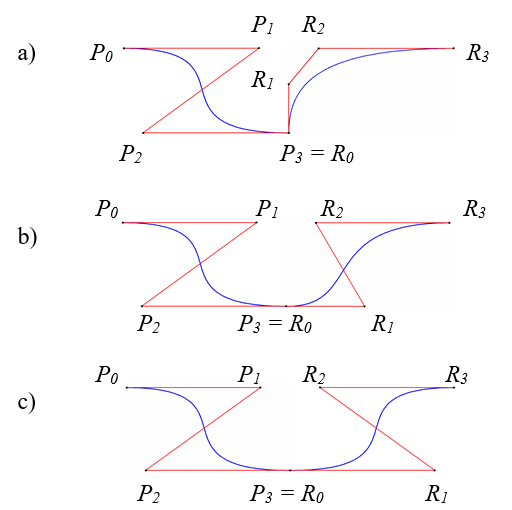
Rys.7.7. Łączenie krzywych Béziera: a) bez zachowania ciągłości, b) z zachowaniem
ciągłości geometrycznej, c) z zachowaniem ciągłości parametrycznej.

W praktyce rzadko kiedy używa się krzywych Béziera wysokiego stopnia. Ponieważ każdy punkt krzywej Béziera zależy od wszystkich punktów kontrolnych, więc w takiej sytuacji trudno byłoby kontrolować kształt krzywej. O wiele prościej jest złożyć całą krzywą z fragmentów, każdy niskiego stopnia.

 Rozpatrzmy dwa segmenty krzywych (rys.7.7)  P0 , P1  , P2 , P3  i  R0 , R1 , R2 , R3 , połączone w punkcie P3 = R0 . 

Jeżeli punkty P2 , P3 = R0 , R1 są współliniowe mówimy o ciągłości geometrycznej G1 krzywej (rysunek 7.7 b).

Jeżeli punkty P2 , P3 = R0 , R1 są współliniowe i sąsiednie odcinki łamanej są równej długości
odległość ( P2 , P3) = odległość (R0 , R1) to mówimy o ciągłości parametrycznej C1 krzywej (rysunek 7.7 c). 

Wymierne krzywe Béziera

Wymierna Krzywa Beziera opisana jest w sposób następujący:

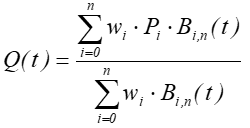 dla 

gdzie    Pi   punkty Beziera  natomiast wi wagi tych punktów. Wartość wagi wpływa na kształt krzywej niezależnie od położenia punktu kontrolnego.

Krzywe wymierne Béziera opisane są w przestrzeni jednorodnej. Oznacza to, że analogicznie do przekształceń geometrycznych opisanych macierzowo w przestrzeni jednorodnej, krzywe płaskie będą opisane w R3, natomiast krzywe trójwymiarowe będą opisane w przestrzeni R4.   

Krzywa taka ma następujące cechy:

  • Dana krzywa może mieć nieskończenie wiele reprezentacji we współrzędnych jednorodnych. Pomnożenie wszystkich wag przez tę samą stałą różną od zera nie zmienia krzywej.
  • Krzywa wymierna jest uogólnieniem krzywej wielomianowej. Dla równej wartości wszystkich wag otrzymujemy krzywą wielomianową Béziera.
  • Jeśli wszystkie wagi są tego samego znaku (wszystkie dodatnie lub wszystkie ujemne), to punkty krzywej leżą w wypukłej otoczce zbioru punktów kontrolnych.
  • Jeśli w0 ≠ 0  to P(0)=P0  oraz jeśli wn ≠ 0  to P(1)=Pn  .
  • Konstrukcja krzywej wymiernej jest niezmiennicza afinicznie. Krzywa wyznaczona na podstawie ciągu punktów kontrolnych jest taka sama jak krzywa wyznaczona na podstawie ciągu punktów kontrolnych poddanych przekształceniom afinicznym.
  • Zmieniając odpowiednio wagi można uzyskać wszystkie krzywe stożkowe. Ta cecha była nieosiągalna w przypadku krzywych wielomianowych Béziera.

 Analogicznie do zwykłej krzywej Béziera, dla krzywej wymiernej istnieje wymierny algorytm de Casteljau wyznaczania punktu na krzywej. Opis algorytmu można znaleźć w książce P.Kiciaka [5].

Dla trzech niewspółliniowych punktów P0 , P1 , P2  jeśli w0=w2=1 , to waga w1 określa rodzaj krzywej stożkowej :

w1 >1                -  łuk hiperboli
w1 =1                -  łuk paraboli (krzywa wielomianowa)
0<w1 <1           -  krótszy łuk elipsy (lub okręgu)
w1 =0                -  odcinek    (sparametryzowany  ze zmienną prędkością)
-1 <w1 <0         -  dłuższy łuk elipsy (lub okręgu)


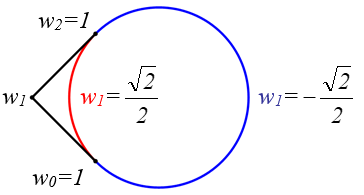
Rys. 7.8. Okrąg reprezentowany w postaci dwóch krzywych wymiernych Béziera.