Podręcznik Grafika komputerowa i wizualizacja
Rozdział 8. MODELOWANIE OBIEKTÓW NATURALNYCH. MODELOWANIE FRAKTALNE I WOLUMETRYCZNE
8.3. Modelowanie fraktalne
Definicja fraktala zaproponowana przez Mandelbrota:
Fraktal to obiekt geometryczny, który:
- Ma cechę samopodobieństwa.
- Jest definiowany rekurencyjnie.
- Ma strukturę trudną do opisania (najczęściej) w ramach geometrii euklidesowej np. wzorem analitycznym.
- Ma (najczęściej) wymiar niebędący liczbą całkowitą.
Twórcą geometrii fraktalnej i samego pojęcia fraktal jest B.Mandelbrot - francuski matematyk polskiego pochodzenia. Przykładem najprostszym iteracyjnie generowanego fraktala jest tak zwana Śnieżynka Kocha zaproponowana przez H. von Kocha w 1904 roku. W każdym kroku iteracji każdy odcinek jest dzielony na trzy części (segmenty) po czym w miejsce jednego segmentu (środkowego) są wstawiane dwa segmenty tworząc z podstawą trójkąt równoboczny. Przy liczbie iteracji dążącej do nieskończoności otrzymuje się figurę, której każdy fragment jest zbudowany dokładnie na tej samej zasadzie (samopodobieństwo) i jednocześnie tak uzyskana krzywa ma nieskończoną długość oraz nie ma stycznej w żadnym punkcie.
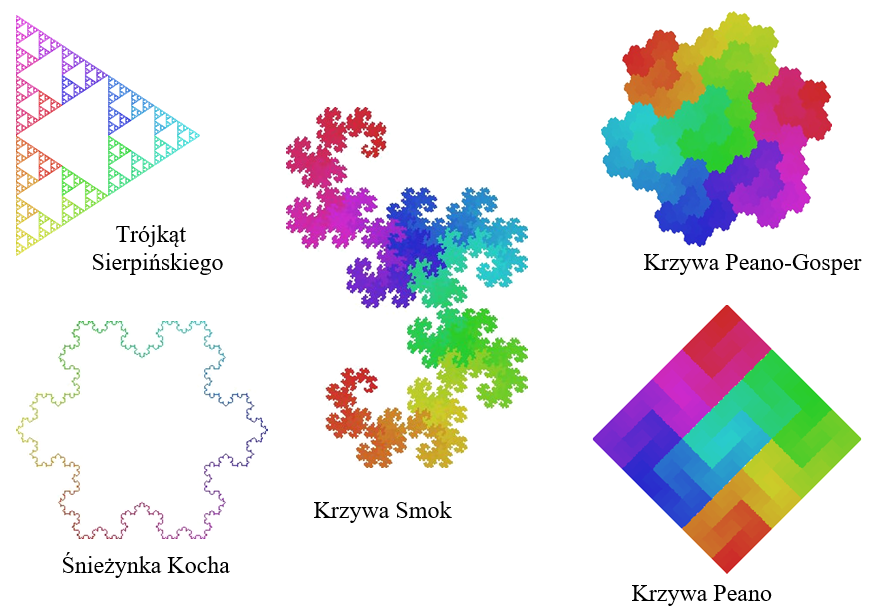
Rys.8.2. Przykłady fraktali definiowanych na płaszczyźnie. Rysunki M.Paterczyka © publikowane za zgodą Autora.
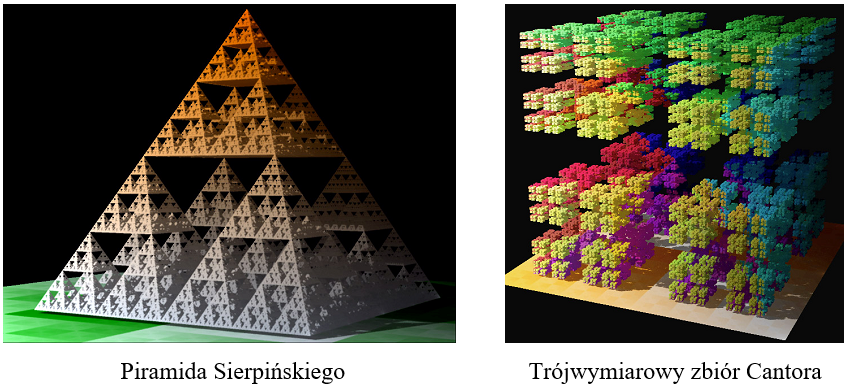
Rys.8.3. Przykłady fraktali definiowanych w przestrzeni
3D.
Rysunki: Solkoll udostępnione w Wikimedii jako public domain.
Problemem pozostaje wymiar takiej krzywej. Dla fraktali określa się wymiar Hausdorffa. F.Hausdorff – matematyk niemiecki zaproponował pojęcie wymiaru jako miarę wzrostu liczby kul (lub kół na płaszczyźnie) o promieniu e potrzebnych do pokrycia danego zbioru przy e dążącym do zera. Wymiar Hausdorffa nigdy nie jest mniejszy niż wymiar topologiczny danego zbioru. Dla fraktali jest liczbą ułamkową. Śnieżynka Kocha (rys.8.2) ma wymiar d=ln4/ln3=1,2618…
Układ funkcji iterowanych
Metryka Hausdorffa określa odległości między zbiorami.
Jeśli rozpatrzymy dwa zbiory A i B, to odległością d(a,B) punktu a ze zbioru A od zbioru B jest najmniejsza odległość spośród odległości tego punktu od wszystkich punktów zbioru B. Odległością d(A,B) zbioru A od zbioru B jest to największa odległość spośród odległości punktu zbioru A od zbioru B.
Metryka Hausdorffa h(A,B) jest określona wyrażeniem: h(A,B)=max(d(A,B), d(B,A))
Atraktory rozpatrywane są w przestrzeni metrycznej zupełnej, w której obowiązuje metryka Hausdorffa.
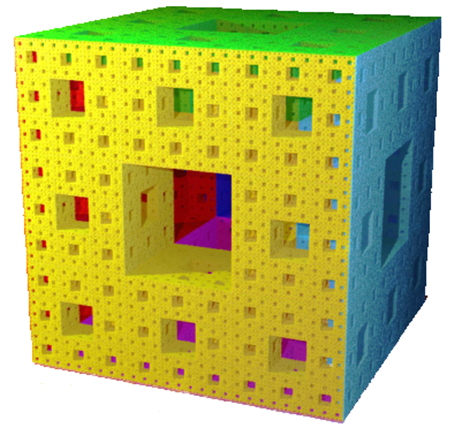
Rys.8.4. Kostka Mengera – przykład atraktora IFS.
Rysunek: Solkoll udostępniony w Wikimedii jako public domain
Bardzo trudno byłoby klasycznymi metodami modelowania (np. CSG lub reprezentacja powierzchniowa) wygenerować obrazy roślin – gałęzi, liści itp. Elementy roślin zachowują samopodobieństwo i podlegają pewnym regułom związanym z rozwojem - wzrostem rośliny. A.Lindenmayer zaproponował w 1969 roku sposób opisu wzrostu oparty na prostych regułach gramatycznych. Taki sposób opisu został nazwany L-systemem lub L-układem. System ten był później rozwijany, między innymi przez A.R.Smitha i P.Prusinkiewicza.
L-systemy służą, przede wszystkim, do opisu wzrostu roślin, kreowania elementów roślinnych, „drzewopodobnych”, korzeni, liści itp. Jest to metoda oparta o aksjomat (pewien ciąg wyjściowy; początkowy) oraz regułę produkcji, która opisuje sposób postępowania w każdej iteracji. Paprotka Barnsleya jest chyba najbardziej znanym przykładem wykorzystania gramatyk do modelowania roślin.

Rys.8.5. Paprotka Barnsleya.
Kolejne kroki budowy obiektu definiowane są zgodnie z zestawem operacji elementarnych. Podstawowy zestaw wprowadzony przez P. Prusinkiewicza wraz z przykładem notacji rozszerzonej przedstawiono w Tabeli 8.1. Na tej samej zasadzie można opisać grafikę żółwia rozkładając ruch pióra na proste reguły sterowania.

(*)Paterczyk M.,
Sawicki D.: Grammar systems for 3d
objects modeling,
Monograph „Computer
Applications in Electrical Engineering”, Politechnika Poznańska 2008, ss.24-31.
W opisie reguł produkcji można także wykorzystać takie atrybuty jak długość i szerokość odcinka czy barwę. Pozwala to dość swobodnie definiować reguły wzrostu.
Warto zwrócić uwagą na fakt, że również fraktale takie jak śnieżynka Kocha czy dywan Sierpińskiego można wygenerować za pomocą L-systemu.
Na przykład dla śnieżynki Kocha z rysunku 8.6 (dla pojedynczego boku startowego trójkąta !)
reguła produkcji: F -> F-F++F-F
gdzie F oznacza ruch do przodu z rysowaniem, - oznacza obrót w lewo o zadany kąt α , + oznacza obrót w prawo o zadany kąt a. Dla śnieżynki Kocha a wynosi 60 stopni.
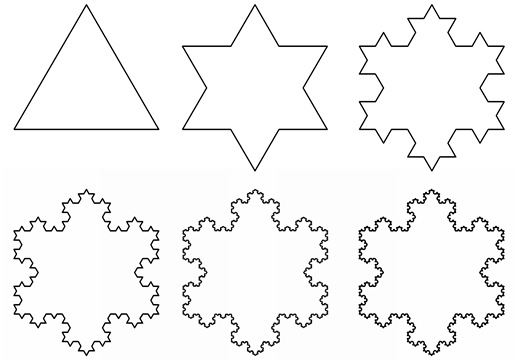
Rys.8.6. Śnieżynka Kocha. Kolejne iteracje.
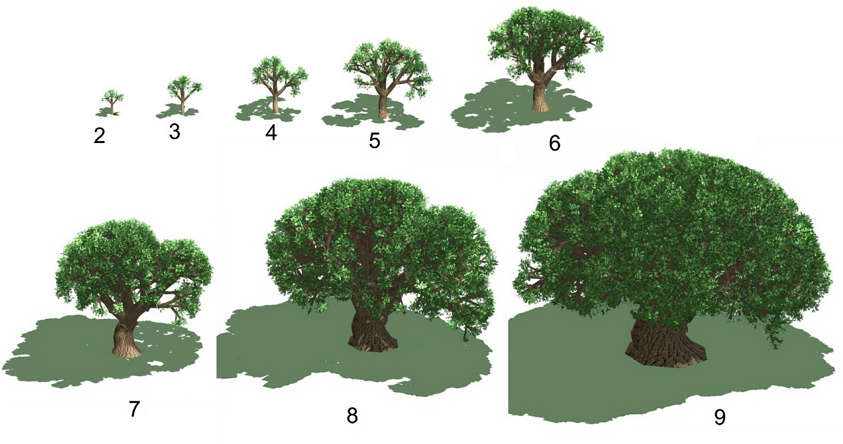
Rys.8.7. Kolejne etapy wzrostu dębu. Rysunki M.Paterczyk © rysunki publikowane za zgodą Autora.
Powstanie L-Systemów związane było z badaniami nad rozwojem organizmów. Tak budowane fraktale znakomicie nadają się do symulacji wzrostu roślin. Rysunek 8.7. pokazuje przykład modelowania wzrostu drzewa: kolejne iteracje odpowiadające kolejnym etapom wzrostu. Warto zwrócić uwagę na fakt, że taki sposób modelowania nie daje możliwości symulacji ciągłego wzrostu (przyrostu) roślin – wzrost jest ściśle związany z kolejnymi iteracjami. A to daje możliwość pokazania określonych stanów rozwoju.
L-system można niezależnie uzupełnić o dodatkowe zasady „obowiązujące” roślinę w trakcie wzrostu. Pozwala to symulować naturalne zjawiska takie jak tropizm (naturalne kierowanie się rośliny w kierunku słońca) i geotropizm (reakcja wzrostowa roślin na siłę ciężkości) – rysunek 8.8.b.
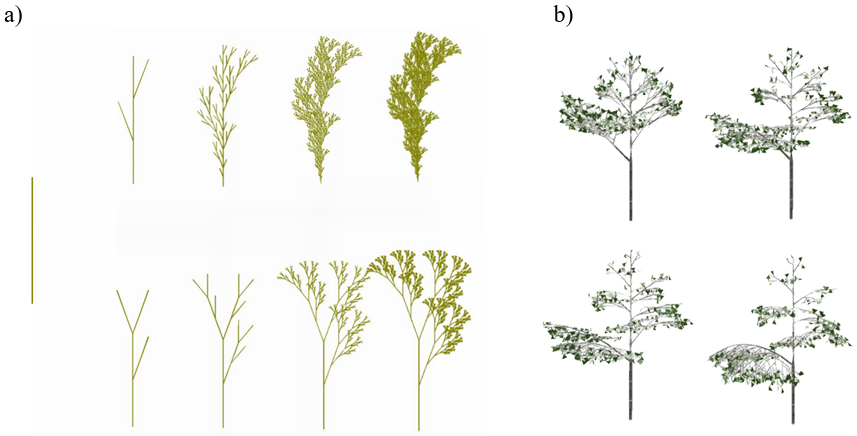
Rys.8.8. Przykład modelowania z wykorzystaniem gramatyk.
a)
Modelowanie gałązki żywotnika – ten sam aksjomat ale różne reguły produkcji.
b)
Wpływ geotropizmu na wzrost i wygląd roślin.
Rysunki Agnieszka Ziemianek ©
rysunki za publikowane za zgodą Autorki.
Pierwotne języki równoległych gramatyk grafowych zostały przez Lindenmayera rozszerzone o dodanie nawiasów (różnych, co daje możliwość rozróżnienia operacji) pozwalających na zagnieżdżanie operacji z wykorzystaniem stosu. L-System odpowiada formalnie gramatyce bezkontekstowej w hierarchii Chomsky’ego. Podstawowa różnica między L-Systemem a gramatyką Chomsky’ego: w L-Systemie produkcja jest stosowana „równolegle” (np. jednocześnie zamienia wszystkie odpowiednie odcinki na krótsze), a nie sekwencyjnie.