Podręcznik Grafika komputerowa i wizualizacja

9.5. Algorytm skaningowy

Algorytm skaningowy (przeglądania liniami poziomymi) jest przykładem algorytmu pracującego w przestrzeni rzutu (działającego z precyzją obrazową). Zasada pracy tego algorytmu oparta jest na założeniu, że w każdym kroku postępowania przeglądana jest jedna linia pozioma obrazu. Można wskazać dwa źródła takiego postępowania. Z jednej strony można bezpośrednio powiązać algorytm z urządzeniem wyświetlającym funkcjonującym na podobnej zasadzie. Przykładem może być monitor, na którym obraz jest powstaje przez generację kolejnych poziomych linii. Z drugiej strony jest to związane z algorytmem wypełniania wielokąta poziomymi liniami. Modyfikując taki algorytm wypełniania można zapewnić dodatkowo eliminację elementów zasłoniętych. Pierwsze artykuły opisujące algorytm tego typu ukazały się w 1967 roku. Autorzy algorytmu skaningowego to Wylie, Romney, Evans, Erdahl.

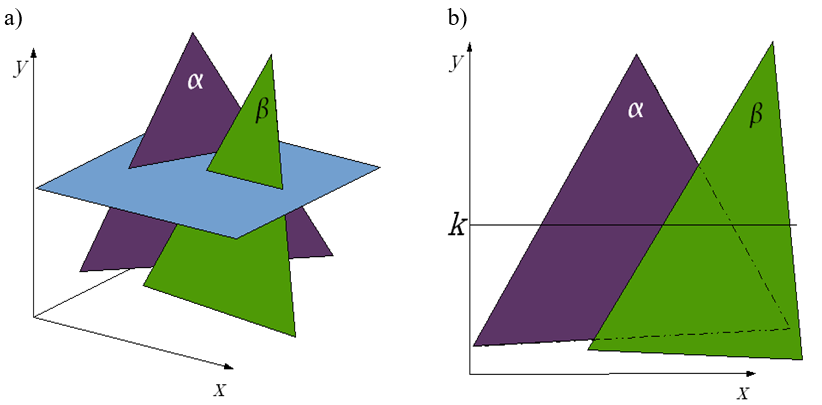
Rys.9.9. Płaszczyzna przecinająca i odpowiadająca jej k-ta linia przeglądanie.

Kolejne linie poziome obrazu można rozpatrywać jako przecięcie ekranu i pewnej płaszczyzny prostopadłej do ekranu – rysunek 9.9. Taka płaszczyzna przetnie wszystkie obiekty sceny. Każda linia obrazu może być rozpatrywana niezależnie. Problem rozstrzygania widoczności można zatem uprościć do niezależnej analizy każdej linii, przechodząc z analizy położenia wielokątów w przestrzeni trójwymiarowej do analizy położenia odcinków na płaszczyźnie.

 

ALGORYTM_SKANINGOWY

1. Posortuj wielokąty pod względem wzrostu max(y) ich rzutów.

2. Przeglądaj kolejne linie obrazu traktując każdą z nich niezależnie.

3. W ramach jednej linii określ dla kolejnych punktów przynależność do odpowiednich wielokątów.

4. W sytuacjach wątpliwych wybierz element najbliższy obserwatorowi.

 Złożoność algorytmu skaningowego O(nlogn), gdzie n — liczba wielokątów

Najczęściej zakłada się, że wielokąty sceny, które podlegają analizie nie przecinają się – chociaż możliwa jest analiza algorytmem skaningowym również i takich przypadków. Dla danej linii analizuje się tablicę krawędzi (przynależności do wielokąta). Tablica ta określa dla danego piksela do rzutu jakich wielokątów ten piksel należy. Najprościej taką tablicę uzyskać traktując linię przeglądania jako prosta przecinana przez krawędzie kolejnych rzutów wielokątów. Podobnie jak w algorytmie wypełniania istnieje problem krawędzi poziomych. Często zakłada się, że bez zmniejszania ogólności można przyjąć, że taki przypadek nie będzie zachodził. Prościej jednak przeanalizować ten przypadek podobnie jak w wypełnianiu wielokąta liniami poziomymi. Mianowicie przyjąć że odcinek poziomy nie tworzy przecięć z linią przeglądająca ale w całości należy do przecinanego wielokąta (rzutu). Natomiast końce odcinka definiują  początek i koniec tej przynależności.

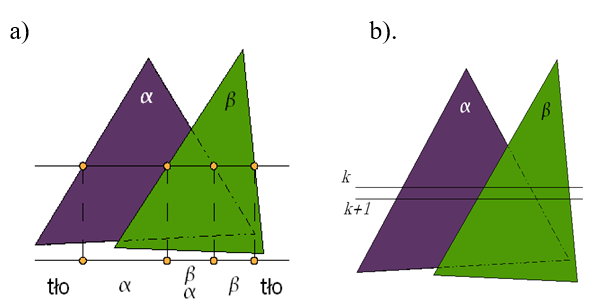
Rys.9.10. a) Analiza kolejnych odcinków linii przeglądania. Każdemu odcinkowi 
jest przypisywany element w przestrzeni,  który może wpływać na widoczność  tego odcinka.
b) Podobieństwo sąsiednich linii.

Analiza widoczności polega na analizie kolejnych odcinków między punktami przecięć w tablicy krawędzi (rys.9.10). Punkty takiego pojedynczego odcinka należą do pewnego zbioru rzutów wielokątów. 

Jeśli ten zbiór jest pusty, to odcinek ten (tzn. odpowiadające mu piksele urządzenia wyświetlającego) należy wypełnić barwą tła.

Jeśli zbiór jest jednoelementowy, to znaczy, że piksele tego odcinka należą dokładnie do jednego rzutu wielokąta. A to oznacza że nie zachodzi żadne zasłanianie i piksele odpowiadające temu odcinkowi należy wypełnić barwą rzutu danego wielokąta.

Jeśli zbiór rzutów jest dwu lub więcej elementowy, to do wypełniania należy użyć barwy tego wielokąta, który jest najbliżej obserwatora. Oczywiście w tym przypadku wybór elementu najbliższego jest bardzo prosty, gdyż rozpatrujemy przecięcia wielokątów i płaszczyzny tnącej, czyli zbiór odcinków na płaszczyźnie.

 Algorytm skaningowy był wielokrotnie usprawniany poprzez dodanie mechanizmów przyspieszających jego działanie. Najciekawszą modyfikacją jest uproszczona analiza sąsiednich linii. Można zauważyć, że najczęściej dla sąsiednich linii schemat przynależności kolejnych pikseli do odpowiednich rzutów nie zmienia się – rysunek 9.10.b. Oznacza to, że można raz zrobić pełną analizę widoczności, a następnie korzystać z niej przy kolejnych liniach przeglądających, dopóki schemat przynależności w tablicy krawędzi się nie zmieni.

Złożoność algorytmu jest taka jak sortowania i wynika z pierwszej fazy algorytmu. Modyfikacje usprawniające (takie jak na przykład uproszczona analiza sąsiednich linii) nie wpływają na złożoność asymptotyczną, ale mogą w określonych sytuacjach przyspieszyć działanie algorytmu.

Algorytm skaningowy rozwiązuje również problem zasłaniania cyklicznego. Ponieważ w pojedynczym kroku analizujemy jedną linię obrazową czyli jedno przecięcie płaszczyzną tnącą, to zasłanianie cykliczne nie stanowi problemu, gdyż na tej płaszczyźnie nie może zachodzić zasłanianie cykliczne odcinków – rysunek 9.11.

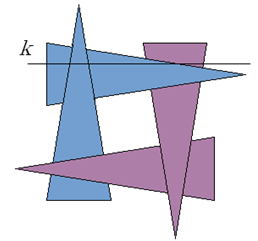
Rys.9.11. Algorytm skaningowy pracuje poprawnie także jeśli zachodzi zasłanianie cykliczne.

Podstawowe właściwości algorytmu skaningowego można scharakteryzować w następujący sposób:

• Zalety
  • Wykorzystuje zalety spójności aby przyspieszyć działanie.
  • Nie wymaga dodatkowej pamięci (poza bieżącą obróbką danych).
  • Jest niewrażliwy na typowe „pułapki” (zasłanianie cykliczne, przenikanie).
• Wady
  • Dość złożony algorytm (geometrycznie).
  • Wymaga analizy położenia wszystkich wielokątów (ich rzutów) przed rysowaniem.
  • Użyteczny w połączeniu ze sprzętem pracującym  w trybie przeglądania linii (skaningowym).