Podręcznik Grafika komputerowa i wizualizacja

9.4. Algorytm malarski

Algorytm malarski (algorytm sortowania ścian) należy do grupy algorytmów z listą priorytetów. Algorytmy te wykorzystują informacje zarówno z przestrzeni obiektu jak i z przestrzeni rzutu (łączą operacje z precyzją obiektową i operacje z precyzją obrazową). Algorytm malarski zaproponowany przez Newella, Newella i Sancha w 1972 roku. Jest jednym z najprostszych opisowo i jednocześnie efektywnym. Polega on na posortowaniu elementarnych fragmentów sceny (wielokątów) zależnie od odległości od obserwatora: od najdalszego do najbliższego. Fragmenty są następnie rysowane w tej kolejności. Zakłada się przy tym, że rysunek powstaje analogicznie do malowania obrazu olejnego (stąd nazwa algorytmu) – rysunek 9.7. Tzn. fragment później namalowany zasłania (zamalowuje) wszystko, co było dotychczas namalowane w tym miejscu. Oczywiście tę cechę ma każde urządzenie wyświetlające (monitor, wyświetlacz LCD), ale stosowanie tego algorytmu bezpośrednio na drukarce byłoby niemożliwe.

Rys.9.7. Powstawanie kolejnych planów na obrazie – idea algorytmu malarskiego eliminacji elementów zasłoniętych.

ALGORYTM_MALARSKI

1. Posortuj wielokąty w kolejności wynikającej z  głębokości (odległości od obserwatora).

2. Rozstrzygnij wszystkie niejednoznaczności.

3. Rysuj w kolejności od najdalszego.

 Złożoność obliczeniowa takiego algirytmu O(nlogn), gdzie n to liczba wielokątów.

Posortowanie  wielokątów jest zadaniem trudnym i może prowadzić do niejednoznaczności. Jeżeli rozpatrzymy dwa wielokąty dowolnie ustawione w przestrzeni, to podstawowym problemem jest ustalenie który z nich jest dalej od obserwatora. To znaczy,. który z nich będzie zasłonięty przez drugi wielokąt z punktu widzenia obserwatora. Żeby to określić stosuje się różne kryteria porównywania położenia. Najprostsze rozwiązanie polega na porównaniu współrzędnych z wielokątów. Jeżeli maksymalna współrzędna z jednego wielokąta jest mniejsza niż minimalna współrzędna z drugiego to pierwszy jest bliżej obserwatora. Oczywiście taki przypadek zachodzi rzadko, najczęściej zakresy współrzędnych wielokątów zazębiają się nie dając możliwości prawidłowego posortowania ich na podstawie takiego kryterium. Lepszym kryterium jest porównanie położenia środków ciężkości wielokątów – bliżej obserwatora znajduje się ten, którego środek ciężkości znajduje się bliżej. Niestety i to kryterium w pewnych sytuacjach zawodzi (czytelnik zechce przeanalizować położenia wielokątów kiedy sortowanie na podstawie położenia środków ciężkości dawałoby niepoprawne rysunki). O wiele lepszym kryterium (chociaż bardziej skomplikowanym obliczeniowo) jest analiza położenia jednego wielokąta względem płaszczyzny wyznaczonej przez drugi wielokąt .Jeżeli pierwszy z nich jest po tej samej stronie płaszczyzny co obserwator, to jest rzeczywiście bliżej obserwatora i nie może być zasłonięty przez drugi wielokąt.

Uwzględniając powyższe rozważania można zaproponować skuteczny algorytm analizy dla algorytmu malarskiego. Dla wielokątów Q i P które mogą się zasłaniać, przeprowadzić zestaw testów. Pierwsze spełnienie testu wyklucza zasłanianie, więc zakończyć testowanie:

TESTY_DLA_ALGORYTMU_MALARSKIEGO

Sprawdzić zasłanianie między wielokątami Q i P:
pierwsza odpowiedź pozytywna wyklucza zasłanianie i kończy test.

1. Czy są otoczenia prostokątne Q i P, które wykluczają zasłanianie ?

2.  Czy rzuty Q i P wykluczają zasłanianie ?

3. Czy P jest w całości po przeciwnej stronie niż obserwator względem płaszczyzny          wyznaczonej przez Q ? Przyjmując, że Q zasłania P !

4. Czy Q jest w całości po tej samej stronie co obserwator względem płaszczyzny wyznaczonej przez P ? Przyjmując, że Q zasłania P !

5. (!) Jeśli żaden z testów 1-4 nie dał pozytywnej odpowiedzi, zamienić wielokąty  rolami, przyjmując że P zasłania Q,  i powtórzyć kroki 3. i 4.

6. (!!) Jeśli również test 5. nie przyniósł rozwiązania, podzielić jeden z wielokątów i przeprowadzić testowanie od początku.

Jednak nawet kryterium wykorzystujące analizę położenia względem płaszczyzny nie radzi sobie w szczególnych przypadkach. Należą do nich: zasłanianie cykliczne i przecinanie się wielokątów (rys.9.8). Pierwszy z nich stanowi tak naprawdę problem w wielu algorytmach rozstrzygania widoczności. Co prawda w praktyce występuje niezmiernie rzadko, ale dobrze skonstruowany algorytm powinien również w takim przypadku pracować poprawnie. (Przykładem występowania zasłaniania cyklicznego może być przysłona obiektywu fotograficznego, której kolejne elementy zachodzą na siebie.) Oba problemy mogą zostać rozwiązanie przez przecięcie jednego z wielokątów na dwie części i potraktowanie każdej z tych części jako niezależnego wielokąta w przeprowadzanej analizie położenia.

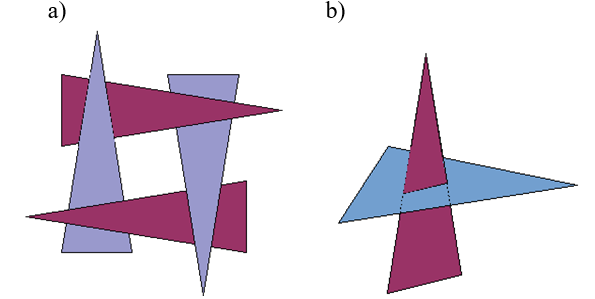
Rys.9.8. Problemy algorytmu malarskiego: 
a) zasłanianie cykliczne, b) przecinanie się wielokątów.

Podstawowe właściwości algorytmu malarskiego można scharakteryzować w sposób następujący:

• Zalety
  • Prosta i zwarta konstrukcja algorytmu.
  • Dość prosty algorytm sortowania.
• Wady
  • Skomplikowane kryteria sortowania aby uzyskać poprawny wynik.
  • Proste sortowanie nie zawsze daje poprawne wyniki (czasem jest to w ogóle niemożliwe ! )
  • Ze względu na skomplikowane kryteria i przypadki sortowanie może zajmować dużo czasu.
  • Konstrukcja algorytmu powoduje wielokrotne wypełnianie tego samego piksela (problemy ze sprzętem )