Podręcznik
1. Programowanie dynamiczne
Programowanie dynamiczne (PD) to metoda wyznaczania rozwiązania problemów optymalizacji dyskretnej dla zadań o specjalnej, dynamicznej, wieloetapowej/sekwencyjnej strukturze.
Bazą PD jest sformułowanie problemu w postaci równania Bellmana. Równanie to jest nazywane też funkcją optymalizacji Bellmana/ programowania dynamicznego. Równanie Bellmana rozwiązuje problem optymalizacji, jeżeli jest on dekomponowalny. Wtedy, rekurencyjnie przeprowadza się wielokrotne rozwiązywanie (dowolną metodą) równania Bellmana.
Nie ma ogólnej metody, procedury wyznaczenia równania Bellmana. Jednak sformułowanie zadania jako programowania dynamicznego jest dość naturalne, gdy wymagane jest wyznaczenie sekwencji decyzji.
Rozważmy prosty przykład, który posłuży nam do wprowadzenia najważniejszych koncepcji podejścia opartego na programowaniu dynamicznym do rozwiązywania problemów wieloetapowych. Poniższy rysunek przedstawia plan ulic łączących dwa punkty, A i L, powiedzmy parkingi w domu i w centrum miasta. Krawędzie odpowiadają ulicom, a węzły skrzyżowaniom.
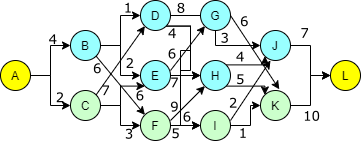
Znany jest czas przejazdu konkretną ulicą, zapisany na rysunku. Do tego znany jest też czas oczekiwania na każdym ze skrzyżowań: B - 5, C - 8, D - 3, E - 3, F - 6, G - 4, H - 2, I - 6, J - 5, K - 3. Naszym zadaniem jest wyznaczenie najkrótszej drogi przejazdu z A do L.
Naiwne podejście mogłoby polegać na wygenerowaniu wszystkich możliwych ścieżek i wybraniu najkrótszej z nich. PD pozwala na zmniejszenie liczby obliczeń, budując optymalne rozwiązanie w sposób systematyczny, sekwencyjnie dokładając kolejne elementy rozwiązania.
Zauważmy, że przejazd z A do L wymaga pokonania 5 ulic, dla każdego układu parametrów czasowych. Można więc powiedzieć, że podróż składa się z 5 etapów, gdzie ostatni etap to osiągnięcie zamierzonego celu. W każdym z wcześniejszych etapów należy podjąć decyzję o wyborze konkretnej ulicy, która doprowadzi nas do kolejnego etapu. Decyzja ta nie zależy od dotychczasowej, przebytej drogi.
Załóżmy, że analizujemy sieć przejazdu wstecz, czyli od ostatniego etapu. Znajdując się w czwartym etapie możemy być na skrzyżowaniu J lub K, przy czym nie mamy wpływu na sposób dostania się do L, bo prowadzi tam tylko jedna ulica. Wiemy natomiast ile czasu zajmie nam dotarcie do L jeżeli znajdziemy się na jednym z tych skrzyżowań: 12 minut jeśli droga biegnie przez J, albo 13 minut jeśli droga biegnie przez K.
Podobną analizę przeprowadzamy teraz w trzecim etapie, dla skrzyżowań G, H, I. Tym razem, znajdując się na konkretnym skrzyżowaniu musimy podjąć decyzję, którą drogę wybrać, aby przejść do następnego etapu, czyli znaleźć się na skrzyżowaniu J lub K. Przy wyborze kierujemy się nie tylko czasem potrzebnym na pokonanie konkretnej ulicy, ale też czasem potrzebnym na dotarcie do celu ze skrzyżowania do którego ta ulica prowadzi. Czyli np. dla skrzyżowania G jasne jest, że lepiej jest wybrać drogę prowadzącą do J, co da w sumie 15 minut do osiągnięcia celu, zamiast drogi do K, co wymagałoby 19 minut na osiągnięcie celu. Gdy doliczymy czas oczekiwania na skrzyżowaniu G to możemy stwierdzić, że droga biegnąca przez to skrzyżowanie będzie wymagać 19( = 15 + 4) minut na dojazd do L. Analogicznie, dla skrzyżowań H oraz I otrzymujemy optymalny czas dojazdu do celu równy: 18 dla H, oraz 20 dla I.
Powtarzamy obliczenia dla kolejnych etapów, aż znajdziemy się w punkcie wyjścia A, czyli niejako etapie zerowym. Można sprawdzić, że najkrótsza trasa wynosi 37 minut.

Znany jest czas przejazdu konkretną ulicą, zapisany na rysunku. Do tego znany jest też czas oczekiwania na każdym ze skrzyżowań: B - 5, C - 8, D - 3, E - 3, F - 6, G - 4, H - 2, I - 6, J - 5, K - 3. Naszym zadaniem jest wyznaczenie najkrótszej drogi przejazdu z A do L.
Naiwne podejście mogłoby polegać na wygenerowaniu wszystkich możliwych ścieżek i wybraniu najkrótszej z nich. PD pozwala na zmniejszenie liczby obliczeń, budując optymalne rozwiązanie w sposób systematyczny, sekwencyjnie dokładając kolejne elementy rozwiązania.
Zauważmy, że przejazd z A do L wymaga pokonania 5 ulic, dla każdego układu parametrów czasowych. Można więc powiedzieć, że podróż składa się z 5 etapów, gdzie ostatni etap to osiągnięcie zamierzonego celu. W każdym z wcześniejszych etapów należy podjąć decyzję o wyborze konkretnej ulicy, która doprowadzi nas do kolejnego etapu. Decyzja ta nie zależy od dotychczasowej, przebytej drogi.
Załóżmy, że analizujemy sieć przejazdu wstecz, czyli od ostatniego etapu. Znajdując się w czwartym etapie możemy być na skrzyżowaniu J lub K, przy czym nie mamy wpływu na sposób dostania się do L, bo prowadzi tam tylko jedna ulica. Wiemy natomiast ile czasu zajmie nam dotarcie do L jeżeli znajdziemy się na jednym z tych skrzyżowań: 12 minut jeśli droga biegnie przez J, albo 13 minut jeśli droga biegnie przez K.
Podobną analizę przeprowadzamy teraz w trzecim etapie, dla skrzyżowań G, H, I. Tym razem, znajdując się na konkretnym skrzyżowaniu musimy podjąć decyzję, którą drogę wybrać, aby przejść do następnego etapu, czyli znaleźć się na skrzyżowaniu J lub K. Przy wyborze kierujemy się nie tylko czasem potrzebnym na pokonanie konkretnej ulicy, ale też czasem potrzebnym na dotarcie do celu ze skrzyżowania do którego ta ulica prowadzi. Czyli np. dla skrzyżowania G jasne jest, że lepiej jest wybrać drogę prowadzącą do J, co da w sumie 15 minut do osiągnięcia celu, zamiast drogi do K, co wymagałoby 19 minut na osiągnięcie celu. Gdy doliczymy czas oczekiwania na skrzyżowaniu G to możemy stwierdzić, że droga biegnąca przez to skrzyżowanie będzie wymagać 19( = 15 + 4) minut na dojazd do L. Analogicznie, dla skrzyżowań H oraz I otrzymujemy optymalny czas dojazdu do celu równy: 18 dla H, oraz 20 dla I.
Powtarzamy obliczenia dla kolejnych etapów, aż znajdziemy się w punkcie wyjścia A, czyli niejako etapie zerowym. Można sprawdzić, że najkrótsza trasa wynosi 37 minut.
Przedstawiona w przykładzie procedura przebiegała sekwencyjnie, w każdym etapie obliczyliśmy optymalne częściowe rozwiązanie, wynikające ze znalezienia się w konkretnym stanie, czyli na konkretnym skrzyżowaniu. Koncepcje te sformalizujemy w następnym podrozdziale.