Podręcznik
1. Programowanie w ograniczeniach
1.1. Backtracking i propagacja
Programowanie w ograniczeniach bazuję na dwóch głównych koncepcjach:- propagacji oraz
- backtrakingu.
Backtracking ekploruje częściowe przypisania do momentu znalezienia kompletnego przypisania. Polega on na inkrementacyjnym budowaniu przypisań częściowych spełniających ograniczenia, zwanych dalej kandydatami na rozwiązanie, oraz odrzucaniu dotychchasowych przypisań częściowych, jeżeli tylko można wydedukować, że nie jest możliwe osiągnięcie rozwiązania (całkowitego przypisania spełniającego wszystkie ograniczenia) przez dalsze budowanie bieżącego kandydata na rozwiązanie. W takiej sytuacji następuje powrót do poprzedniego kandydata i podjęcie próby utworzenia z niego innego rozwiązania. Wnioskowanie o możliwości dalszego budowania rozwiązania jest oparte o propagację, która polega na eliminacji wartości z domen zmiennych, które nie mogą być przyjęte ze względu na ograniczenia przy bieżącym stanie kandydata. Rozważmy przykład problemu czterech hetmanów, których należy rozstawić na planszy o wymiarach 4x4, tak, aby w żadnym wierszu, kolumnie oraz przękątnych był doładnie jeden hetman.
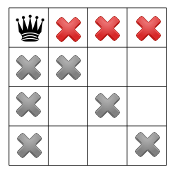
Załóżmy, że algorytm wybiera kolejne wolne miejsce, na przykład tak, jak ma to miejsce na poniższym rysunku:

co powoduje, że nie jest możliwe wstawienie czwartego hetmana, gdyż po wstawieniu trzeciego hetmana, domena dla zmiennej reprezentującej ustawienie czwartego hetmana stała się pusta.
Algorytm dokonuje teraz backtrakingu i wraca do sytuacji po pierwszym kroku, ale teraz już wie, że wstawienie drugiego hetmana w trzecim wierszu prowadzi do niedopuszczalności. Dlatego algorytm próbuje wstawić drugiego hetmana w czwartym wierszu.