Drukuj ten rozdziałDrukuj ten rozdział

Podręcznik

1. Podstawy programowania matematycznego

1.4. Wypukłość w optymalizacji

Wprowadzimy teraz serię podstawowych pojęć, w szczególności związanych z wypukłością, która jest niezmiernie ważna w problemach optymalizacji.

 

Problem decyzyjny – jest to problem, który odpowiada tak/nie na postawione pytanie, np. mając dwie liczby x i y, czy x jest dzielnikiem y?
 Problem funkcyjny – problem, w którym odpowiedź może być bardziej złożona i przyjmuje wartość pewnej funkcji, np. mając dwie liczby x i y, jaki jest wynik dzielenia y przez x?
 Problem optymalizacyjny – problem polegający na wyszukaniu najlepszej odpowiedzi, np. mając dwie liczby x i y, wyznaczyć największy wspólny dzielnik.

 Złożoność obliczeniową problemów definiujemy w ramach klas złożoności.

Klasa P – problemy rozwiązywalne w czasie wielomianowym (na maszynie Turinga)
Klasa NP – problemy weryfikowalne w czasie wielomianowym na maszynie Turing, a rozwiązywalne w czasie wielomianowym na niedeterministycznej maszynie Turinga (maszynie z wyrocznią)
Klasa NP-zupełnych – problemy z NP., takie, że dowolny problem z NP może być zredukowany do problemu w klasie NP-zupełnej w czasie wielomianowym.
NP-trudny – problem co najmniej tak trudny jak każdy problem z klasy NP (ale potencjalnie jeszcze trudniejszy)

 


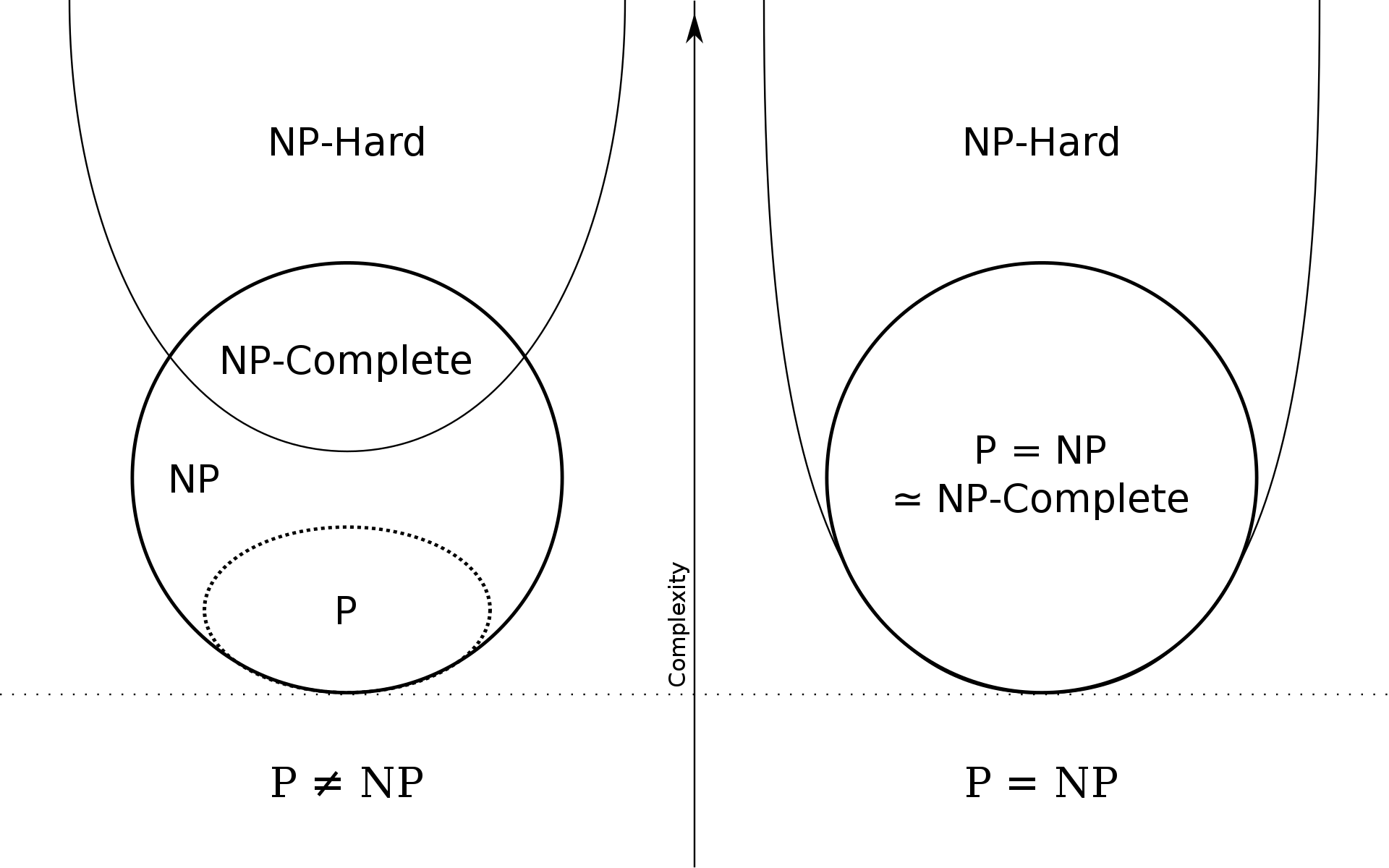
 źródło: wikipedia


Optymalizacja (programowanie matematyczne)
\min_x f(x)
p.o.
x \in \mathcal{F}

Skrót “p.o” należy czytać „przy ograniczeniach”. W modelu x \in \mathbb{R}^n to zmienne decyzyjne. Zmienne x mogą być ciągłe lub dyskretne.  \mathcal{F}  \subset \mathbb{R}^n to zbiór rozwiązań dopuszczalnych. Jego opis może przyjmować postać zbioru funkcji liniowych lub zbiór funkcji wypukłych. W niektórych sytuacjach może nie być podany jawnie, a np. być dostępny przez algorytm/symulacje. Funkcja celu to  f:\mathcal{F} \mapsto \mathbb{R}.

 Tak ogólnie postawiony problem może być trudny do rozwiązania, a czasem nawet znalezienia rozwiązania dopuszczalnego jest kłopotliwe. Dlatego szczególnie interesuje nas znajomość przynależności danego problemu/modelu do klasy problemów, które mogą być efektywnie rozwiązywane. Do problemów łatwych należy zaliczyć np. zadania programowania liniowego (ze zmiennymi ciągłymi) oraz modele sieci przepływowych. Są to przykłady problemów wypukłych (lub możliwych do uwypuklenia). Generalnie optymalizacja wypukła jest zadaniem, które można efektywnie rozwiązać. Stąd ważkość zagadnienia wypukłości, którą dalej poruszamy.

 

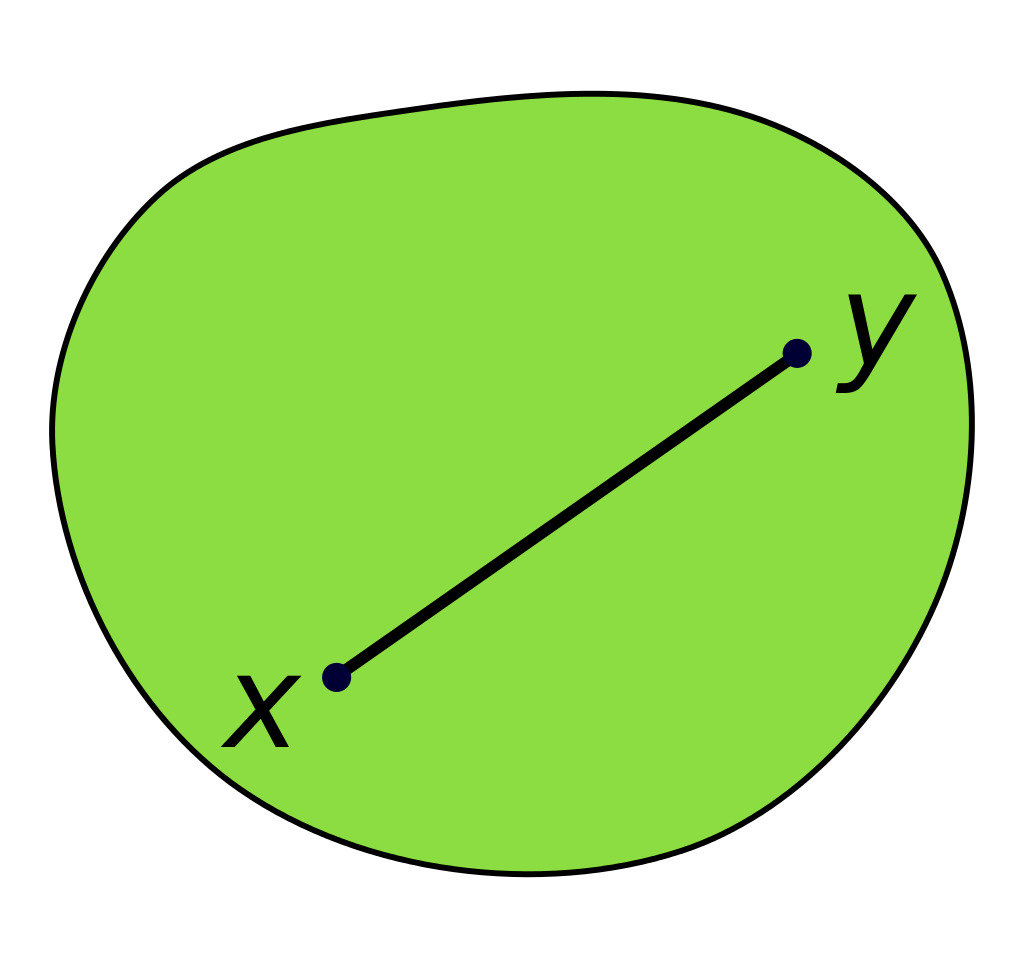
Zbiór wypukły – jeżeli dla dwóch dowolnych punktów zawartych w zbiorze, odcinek łączący te punkty również zawiera się w zbiorze.

Przyładowy zbiór wypukły:


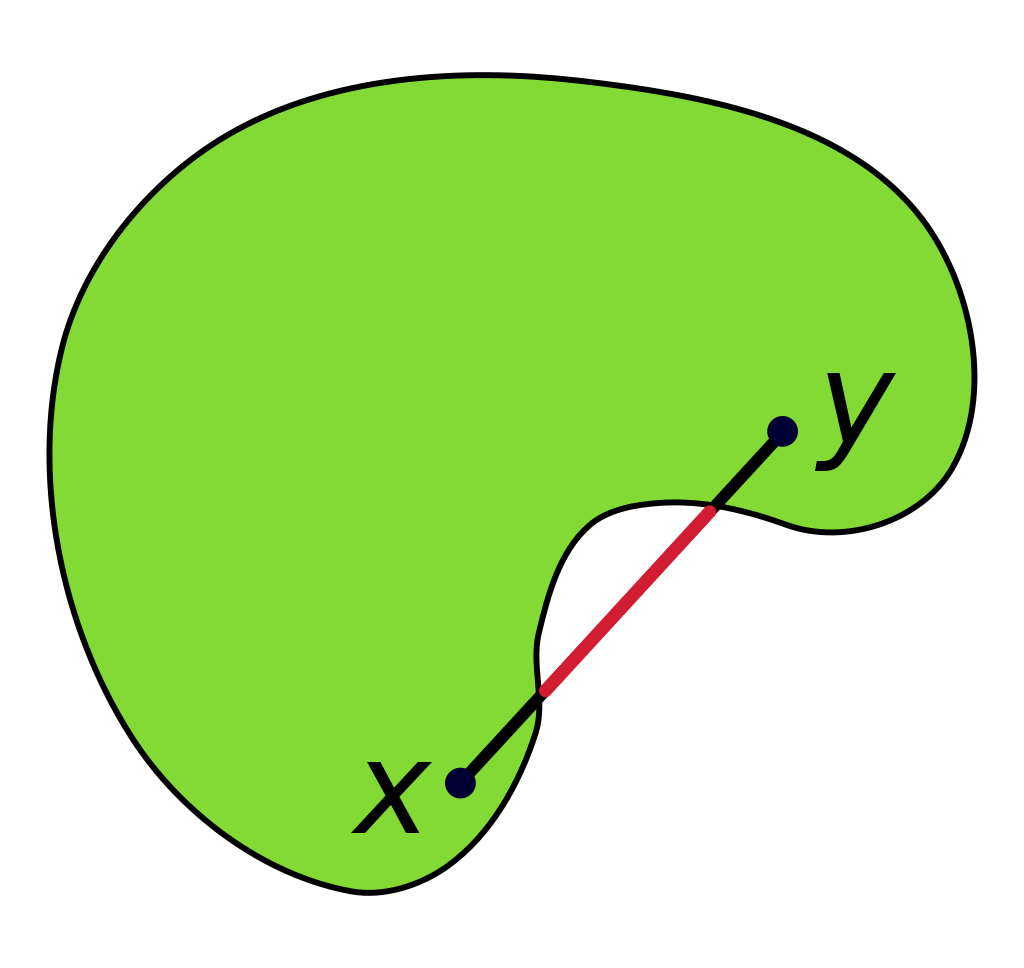
Oraz przykład zbioru niewypukłego:


 

Przykłady innych zbiorów wypukłych:

Odcinek


Prosta


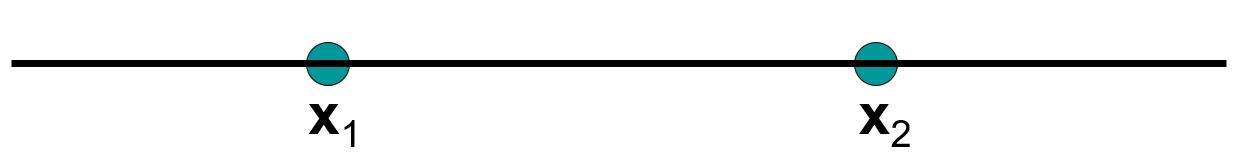
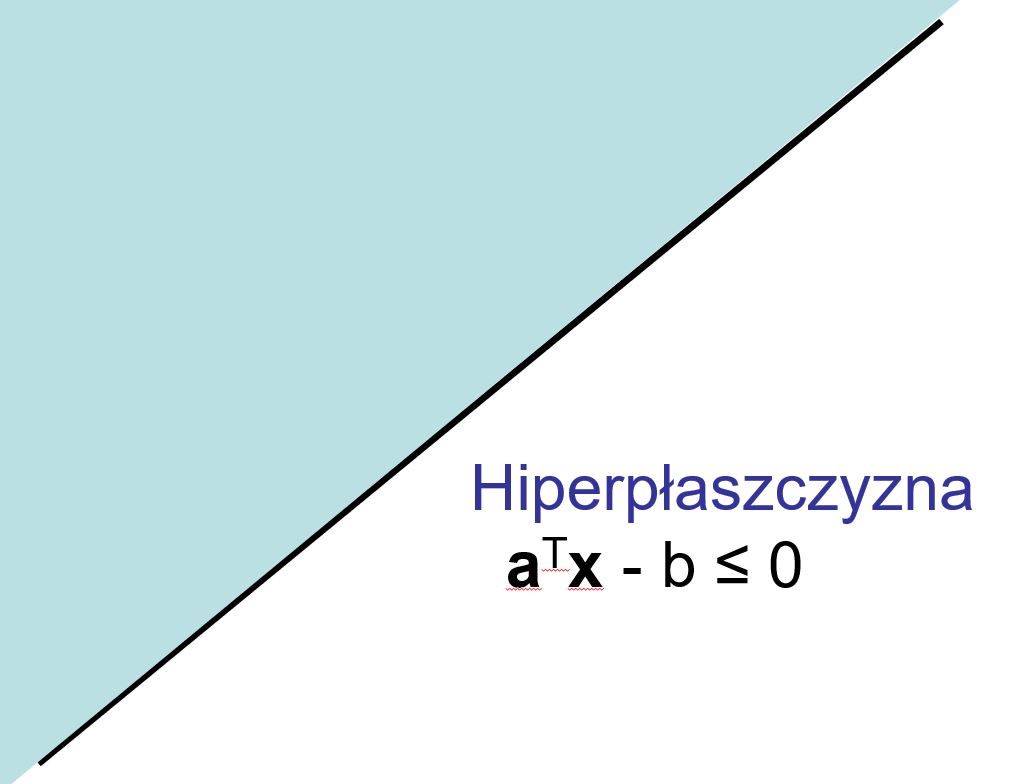
Hiperpłaszczyzna


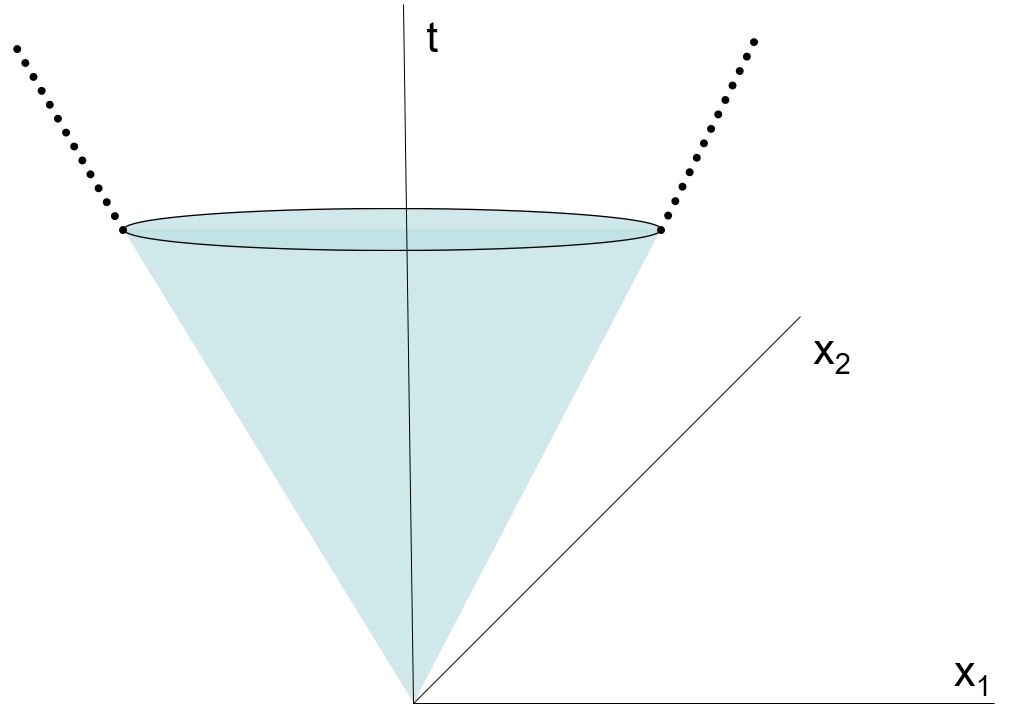
Stożek

 


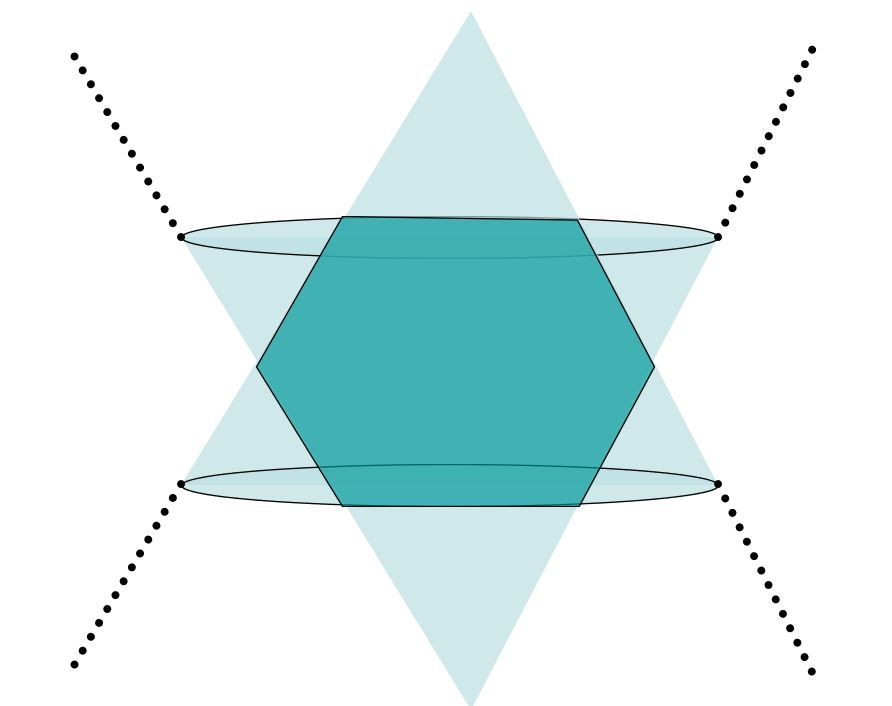
Niektóre operacja na zbiorach mogą zachowywać wypukłość. Przykładowe operacje zachowujące wypukłość:

Przecięcie zbiorów


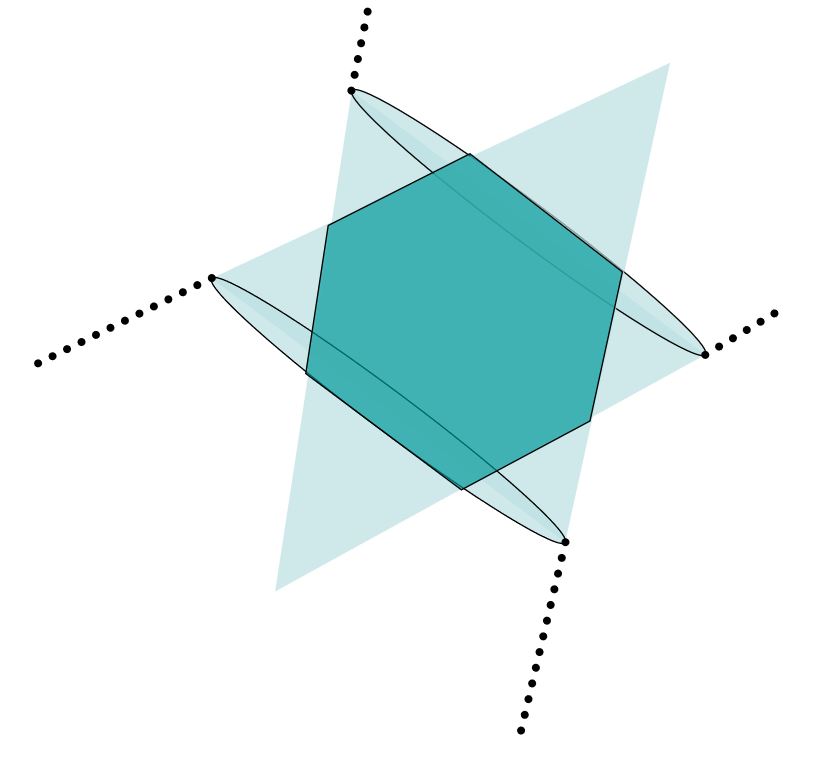
Przekształcenie afiniczne x \longmapsto Ax + b


 

Otoczka wypukła zbioru X to najmniejszy zbiór wypukły zawierający X.
\texttt{conv } X = \bigcap\{M: X\subset M \wedge M \texttt{ jest wypukły}\}

 Otoczka wypukła jest szczególnie ważna w przypadku zbiorów dyskretnych


 

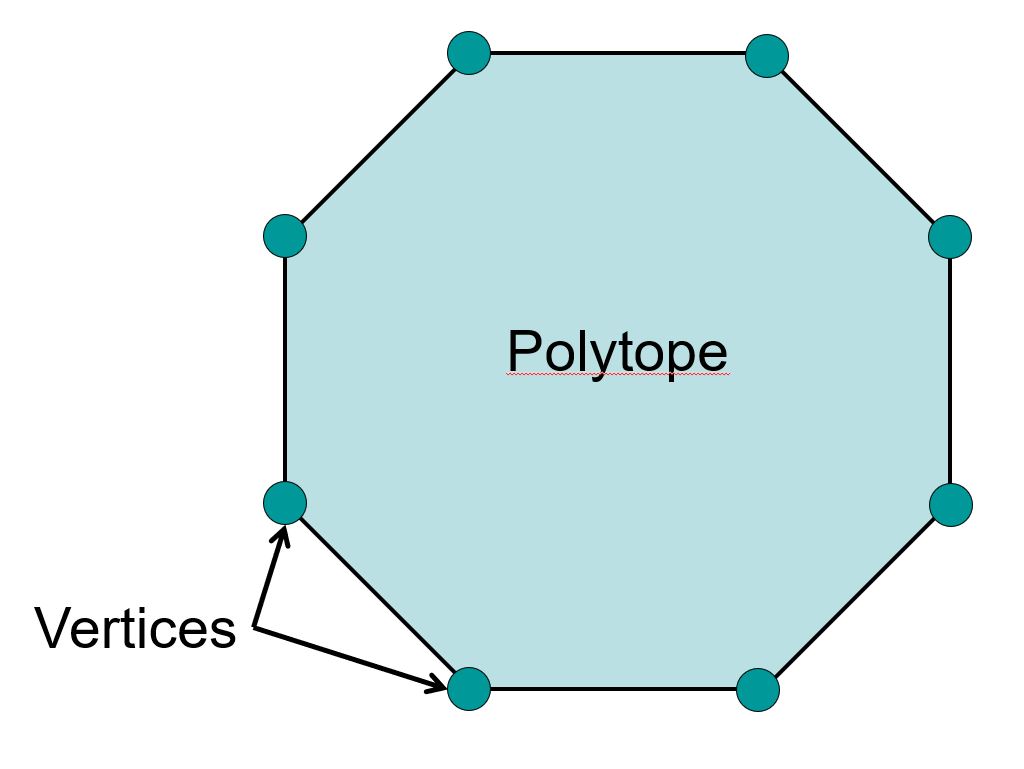
Funkcja g: X \longrightarrow \mathbb{R} określona na zbiorze wypukłym X jest wypukła, jeżeli dla każdego 0 \leq t \leq 1$ i $x_1, x_2 \in X spełniona jest nierówność

g(tx_1+(1-t)x_2) \leq tg(x_1)+(1-t)g(x_2), co obrazuje poniższy obrazek

 

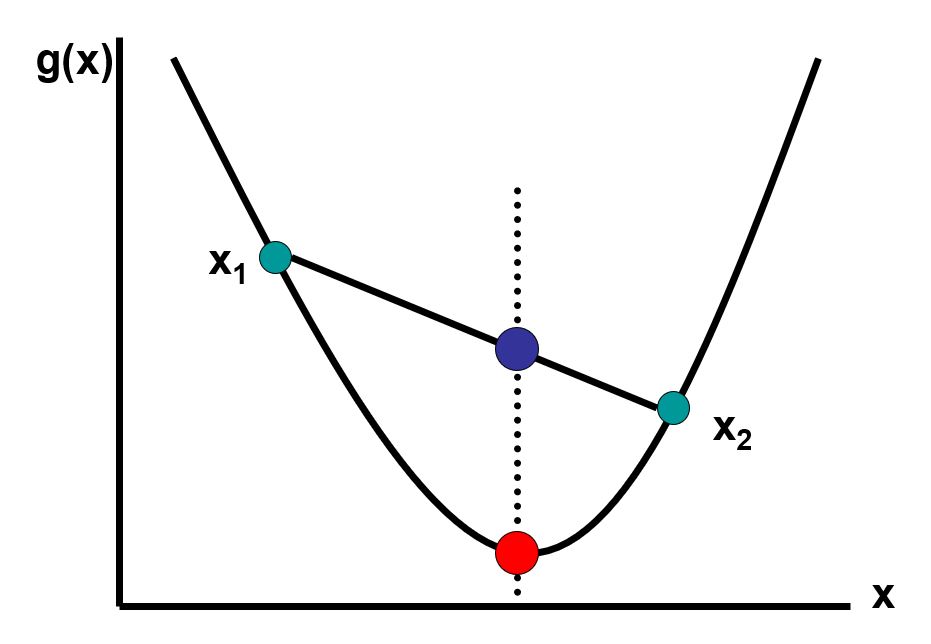
Funkcja jest wypukła, jeżeli jej nadgrafik jest zbiorem wypukłym:


 

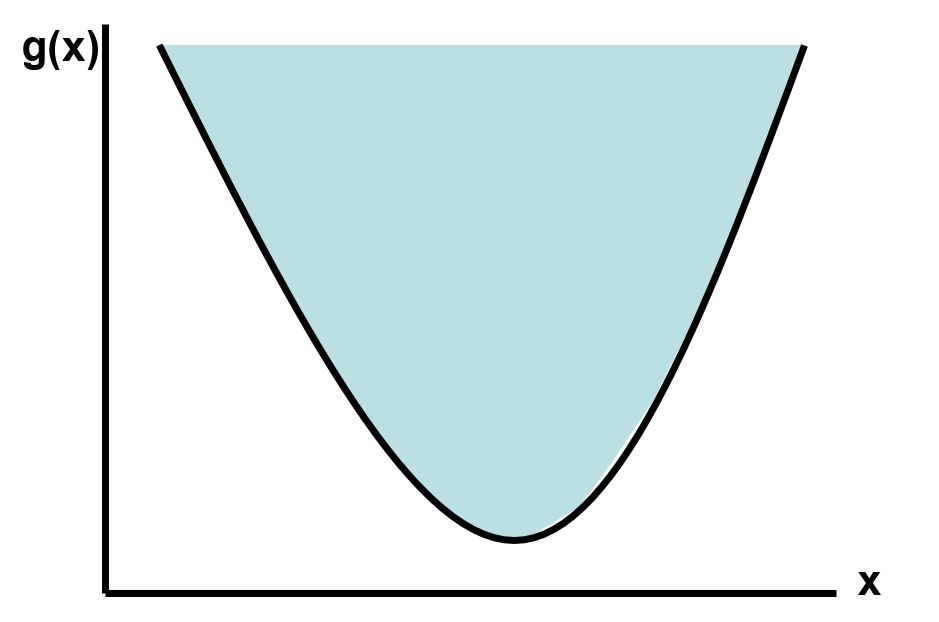
Równoważnie można powiedzieć, że funkcja jednokrotnie różniczkowalna jest wypukła jeżeli zachodzi poniższy warunek:


Zaś dla funkcji podwójnie różniczkowalnej musi zachodzić następujących warunek dla hesjanu:

H(x) \succeq 0

 

Istnieją operacje, które zachowują wypukłość.

Nieujemna suma ważona:


 

Maksimum funkcji


 

Optymalizacja wypukła
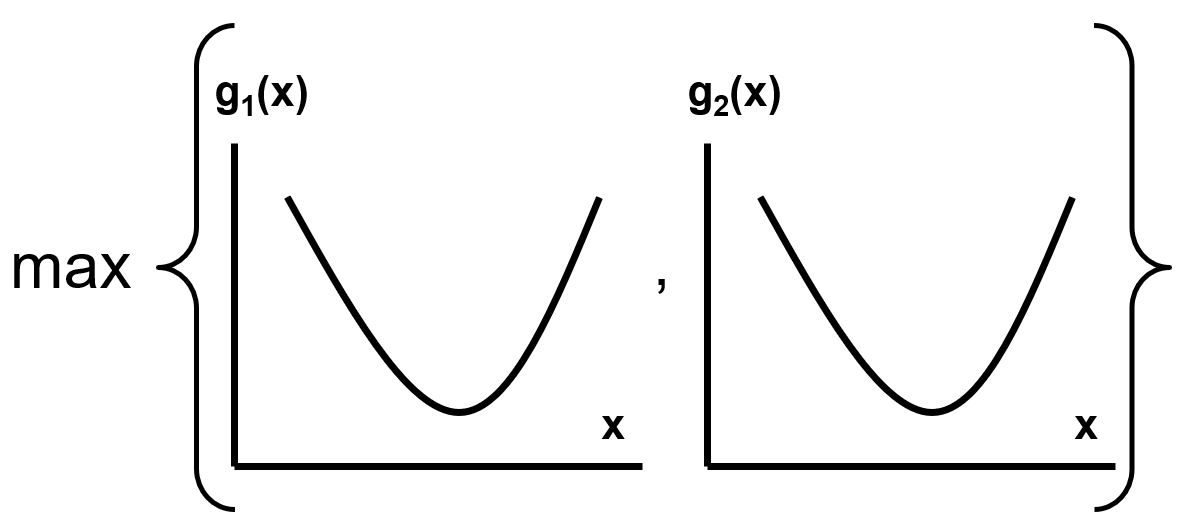
Funkcja celu wypukła i zbiór rozwiązań dopuszczalnych wypukły.
\min f_0(x)
p.o.
f_i(x) \leq 0, \qquad i=1,\ldots,m
a^T_ix=b_i, \qquad i=1, \ldots, p
gdzie f_0, f_1, \ldots, f_m$ są wypukłe, a ograniczenia równościowe afiniczne.

 Dla optymalizacji wypukłej lokalne optimum jest również optimum globalnym.