Podręcznik

2. Modelowanie zależności

2.10. Wypukłe i niewypukłe funkcje odcinkami liniowe

Rozważamy modelowanie funkcji jednej zmiennej, odcinkami liniowej.

Przykładowo, funkcja odcinkami liniowa może być aproksymacją funkcji nieliniowej, jak na poniższym rysunku: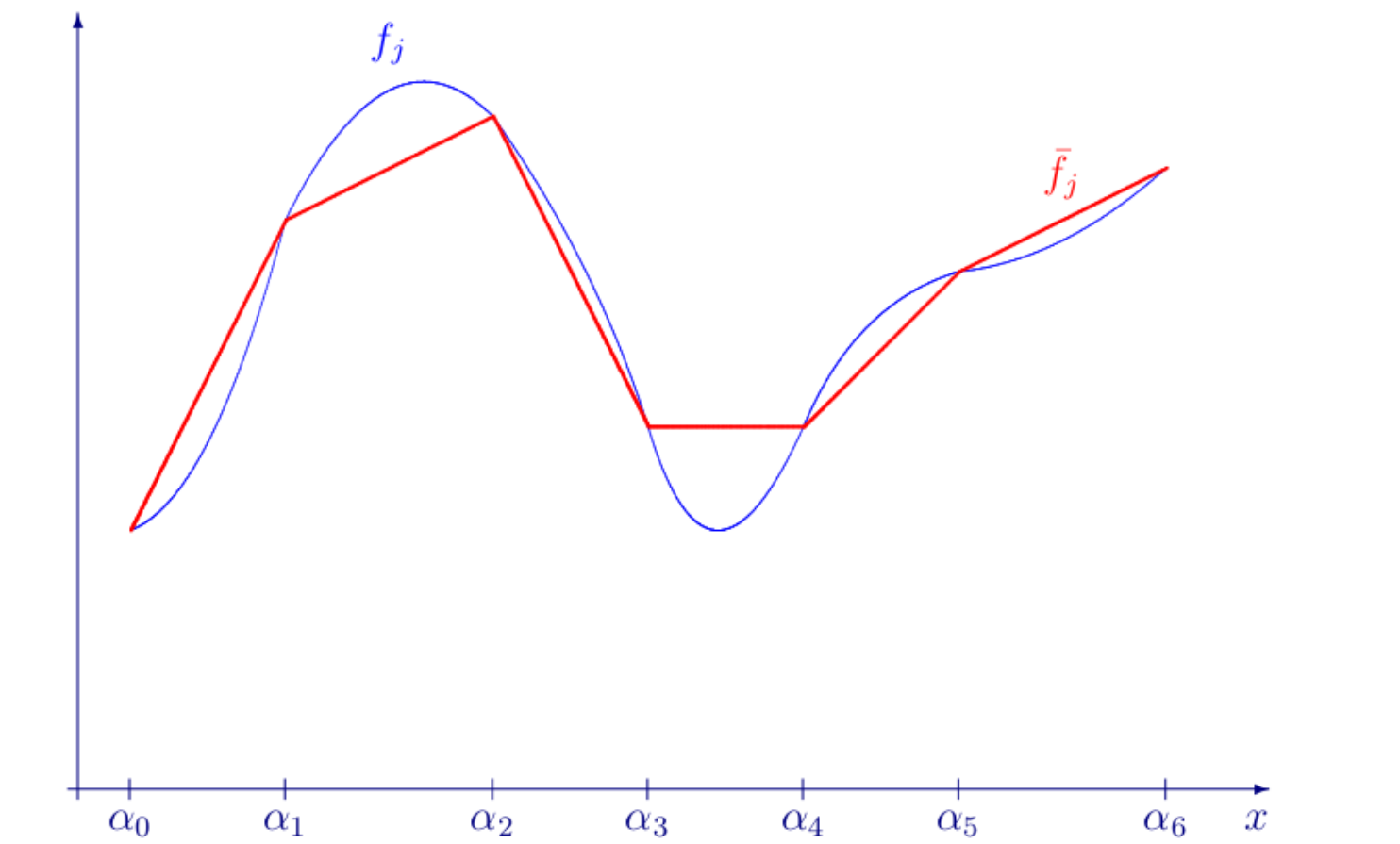

W ogólnym przypadku, model funkcji odcinkami liniowej jest liniowy całkowitoliczbowy. Jednak w niektórych przypadkach modelowanie odbywa się wyłącznie przy pomocy zależności linowych z ciągłymi zmiennymi. Dotyczy to sytuacji gdy maksymalizowana jest funkcja wklęsła lub minimalizowana funkcja wypukła.

Modele liniowe ciągłe

Niech funkcja przedziałami liniowa będzie opisana następującymi równaniami:

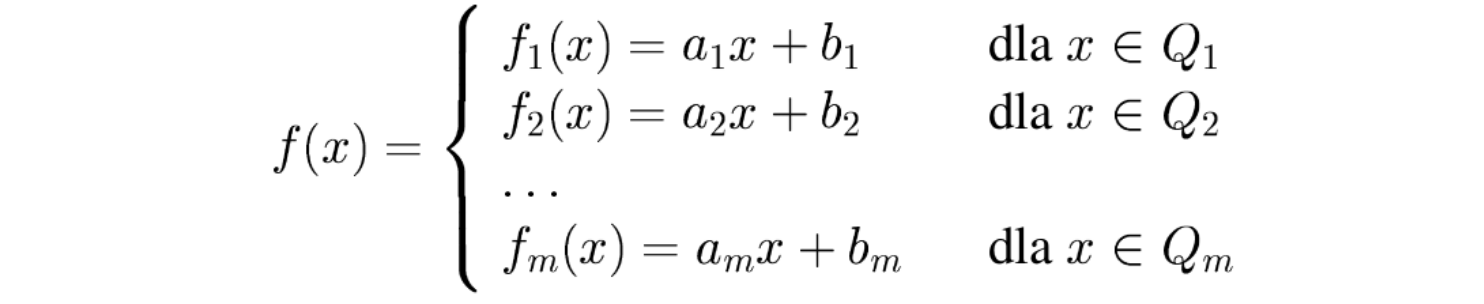
i funkcja

$f(x)$ jest wklęsła czyli:

Wtedy, dla zadania maksymalizacji, może być ona modelowana następująco:

Możliwe jest też wykorzystanie innego podejścia, tzw. przyrostowego, w którym pomocnicze zmienne $x_i$ oznaczają przyrost argumentu w i-tym przedziale. Wtedy funkcja odcinkami liniowe jest wyrażona następującymi zależnościami:

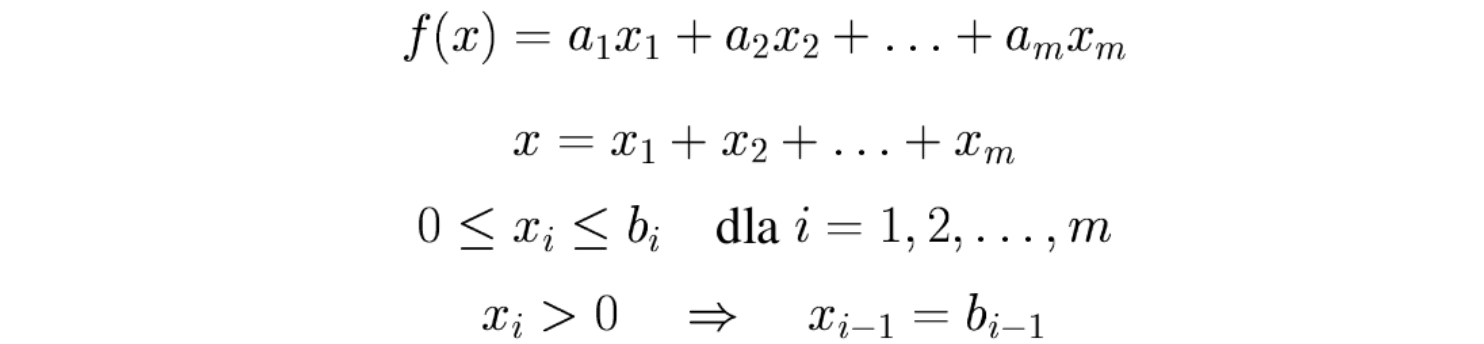
gdzie w przypadku wklęsłej funkcji $f(x)$ zachodzi następująca własność:

jak na poniższym rysunku:

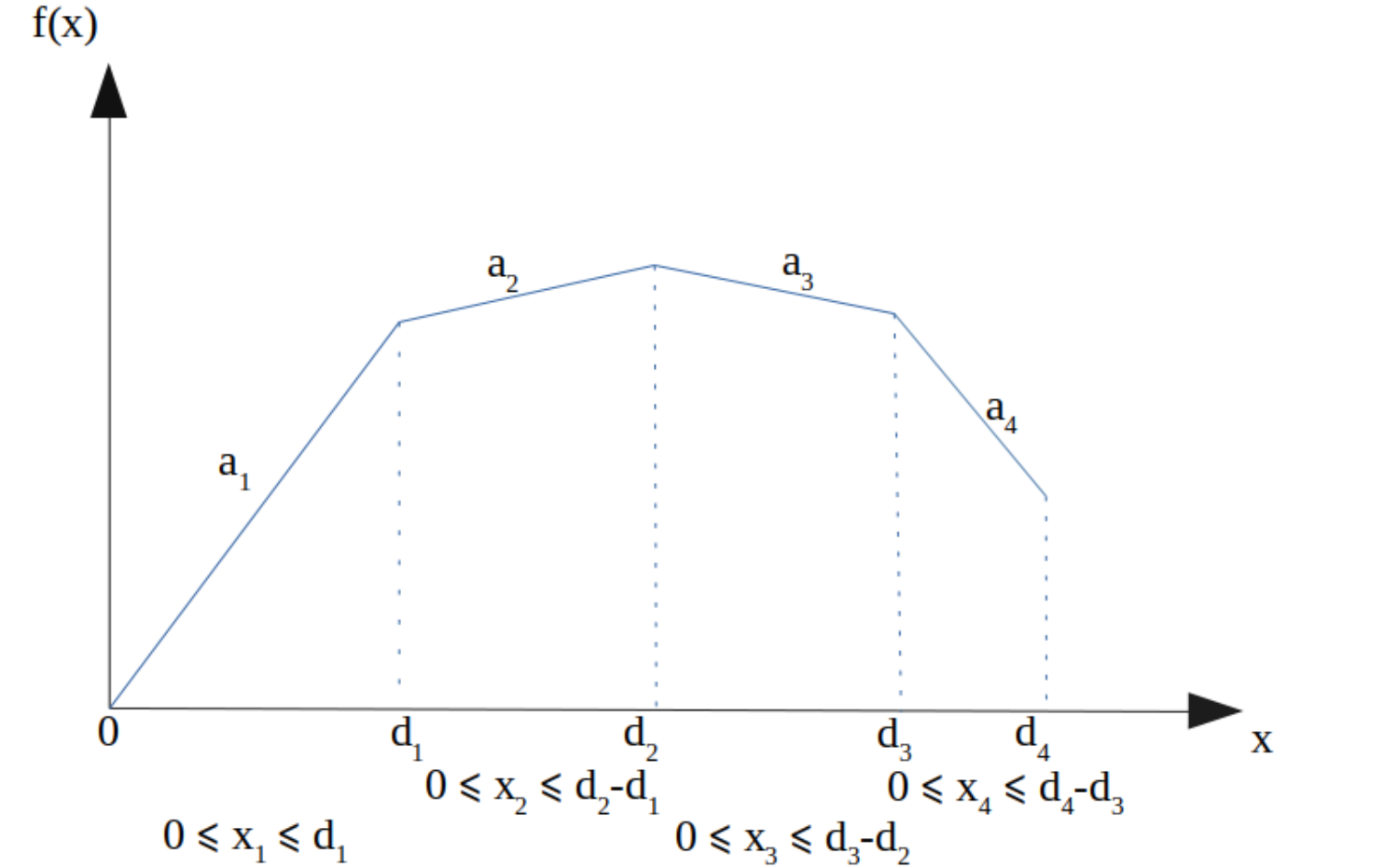
Wtedy funkcja $f(x)$ może być modelowana w następujący sposób:

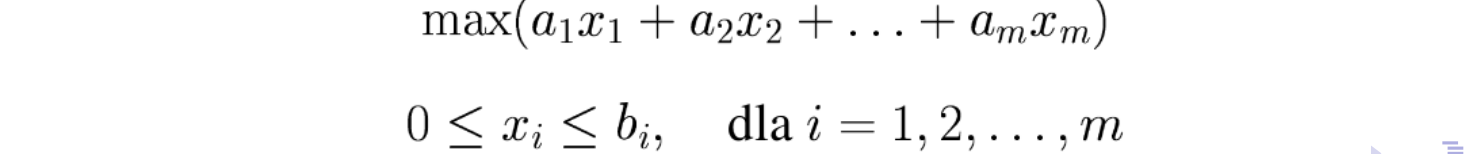
Modele liniowe całkowitoliczbowe

W sytuacji, gdy jest maksymalizowana funkcja wypukła lub minimalizowana funkcja wklęsła, konieczne jest zastosowanie modelu całkowitoliczbowego. Należy pamiętać, że modele całkowitoliczbowe są znacznie trudniejsze jeśli chodzi o ich rozwiązywanie, w związku z tym należy ich używać tylko w sytuacjach niezbędnych.

Rozważmy znowu funkcję przedziałami liniową:

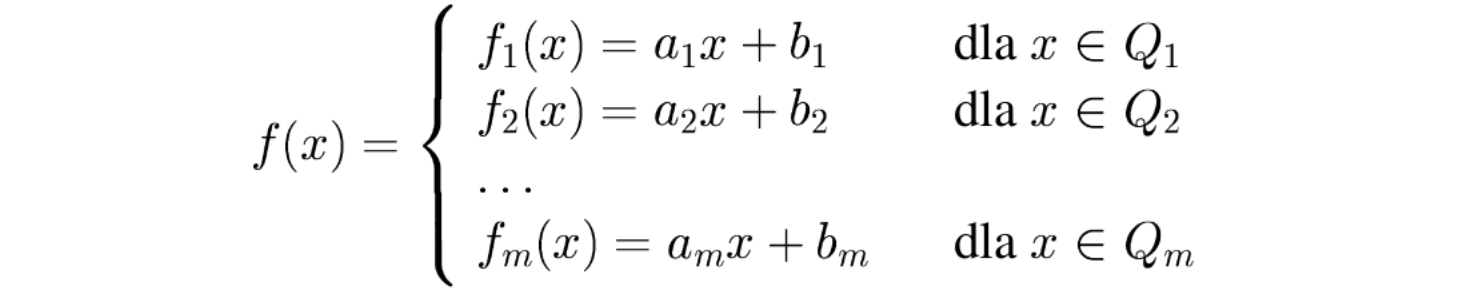
Tym razem jednak, jest ona wypukła, czyli:

Model programowania matematycznego tej funkcji zawiera już zmienne całkowite/binarne ( $y_i$ ) i może być przedstawiony następująco:

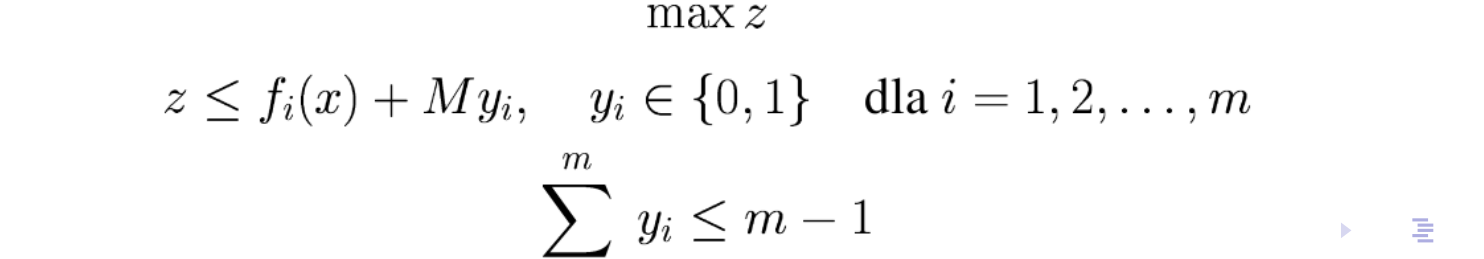
Wersja przyrostowa jest zbliżona do funkcji wklęsłej, ale zawiera dodatkowe zmienne binarne, wymuszające właściwą kolejność ustalania zmiennych reprezentujących przyrosty:

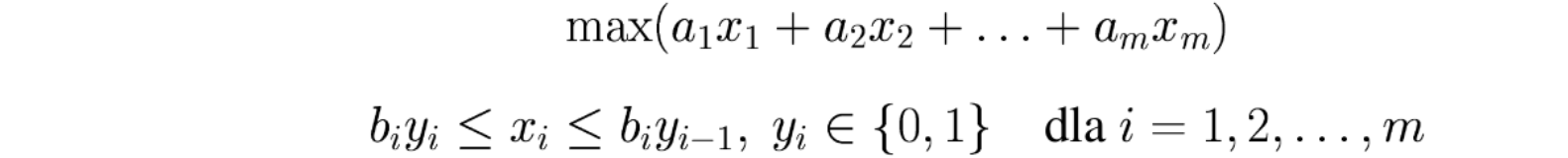
Zaletą modelu przyrostowego jest to, że może być użyty do dowolnej konfiguracji funkcji odcinkami liniowej, która miejscami jest wklęsła a miejscami wypukła. Nie jest to prawdą dla standardowej postaci, która działa prawidłowo tylko dla funkcji wypukłej.