Podręcznik

Zbiór rozmyty

Zbiór rozmyty \(A\) w przestrzeni rozważań \(\mathbb{X}=\{x\}\) (czyli zbiór rozmyty \(A\) w \(\mathbb{X}\)) jest zbiorem par:

$$

A = \{(\mu_A(x),x)\}

$$

Nośnik zbioru rozmytego (ang. support) $A$ w \(\mathbb{X}\) jest zdefiniowany jako zbiór nierozmyty ( \( \emptyset \subseteq supp A \subseteq \mathbb{X}\)):

$$

supp A = \{x \in \mathbb{X}: \mu_A(x) > 0\}

$$

\(\alpha\)- przekrój zbioru rozmytego \(A\) w \(\mathbb{X}\) jest zdefiniowany jako zbiór nierozmyty:

$$

A_{\alpha} = \{x \in \mathbb{X}: \mu_A(x) >  \alpha \}, \quad \alpha \in (0,1]

$$

Rodzaje funkcji przynależności:

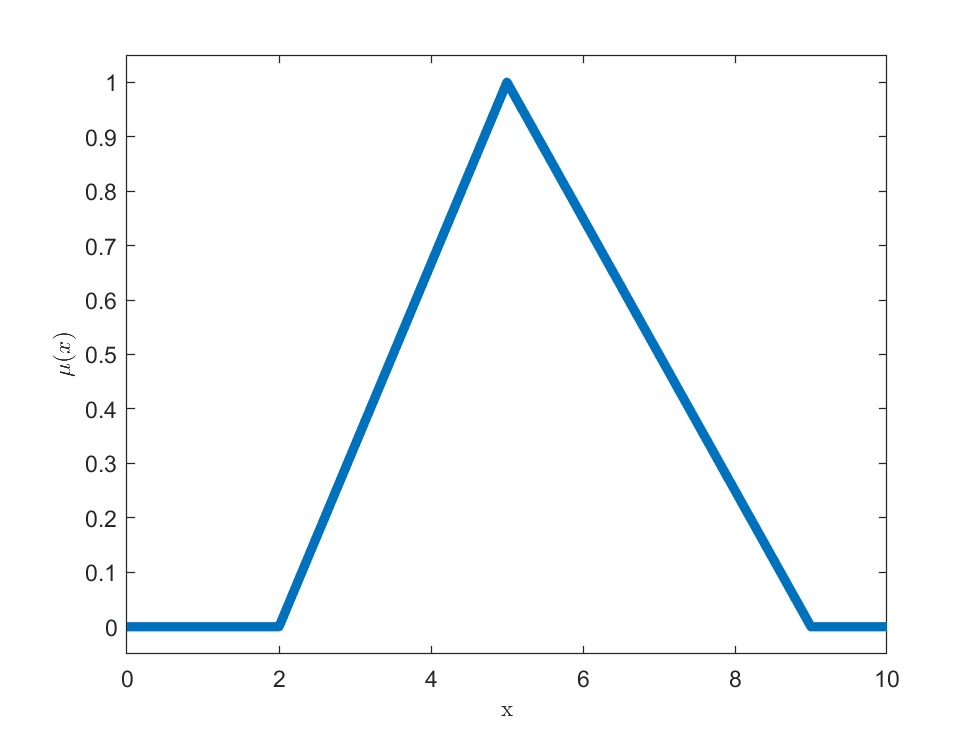
• Trójkątna funkcja przynależności
• Trapezoidalna funkcja przynależności
• Gausowska funkcja przynależności
• Dzwonowa funkcja przynależności
• Sigmoidalna funkcja przynależności

$$\mu_(x,a,b,c)=\left\{\begin{array}{rcl}

0&& x < a\\

\frac{x-a}{b-a}&& a \leq x \leq b\\

\frac{c-x}{c-b}&& b \leq x \leq c\\

0&& x > c

\end{array} \right.$$

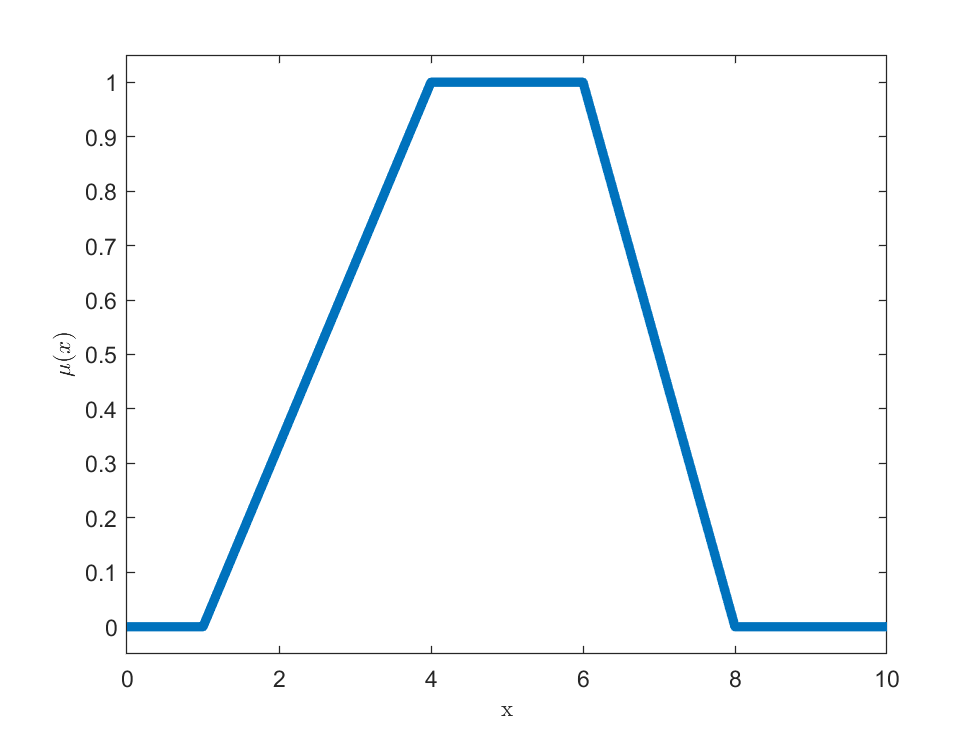
Trapezoidalna funkcja przynależności:

$$\mu_(x,a,b,c,d)=\left\{\begin{array}{rcl}

0&& x < a\\

\frac{x-a}{b-a}&& a \leq x \leq b\\

1&&b \leq x \leq c\\

\frac{d-x}{d-c}&& c \leq x \leq d\\

0&& x > d

\end{array} \right.$$

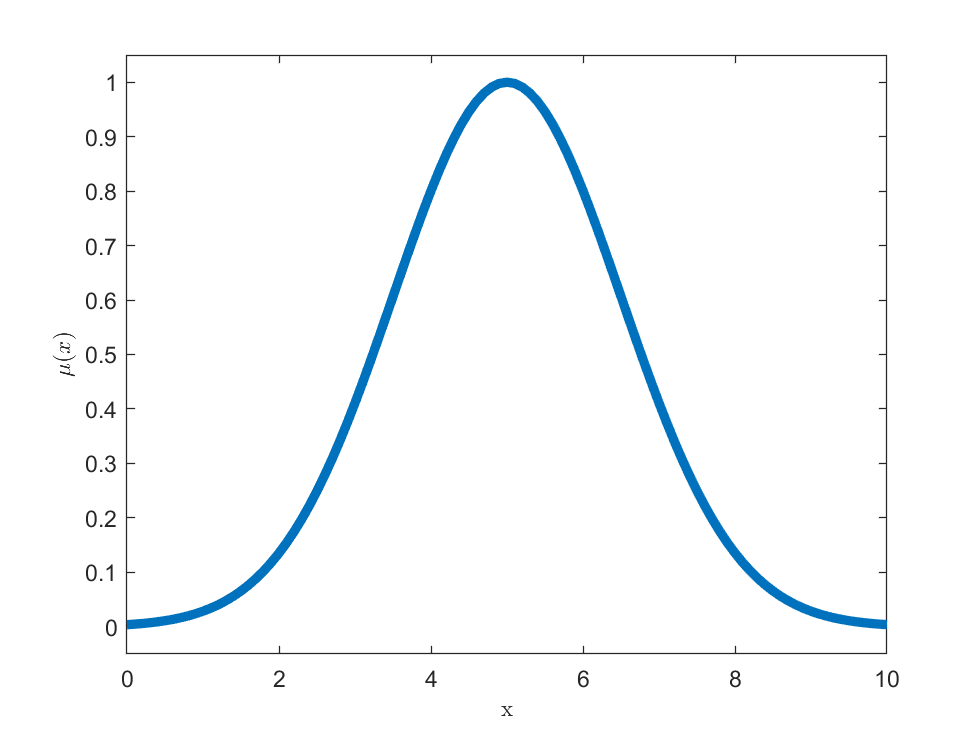
Gausowska funkcja przynależności

$$

\mu_(x,\sigma,c)= \exp(\frac{-(x-c)^2}{2 \sigma^2})

$$

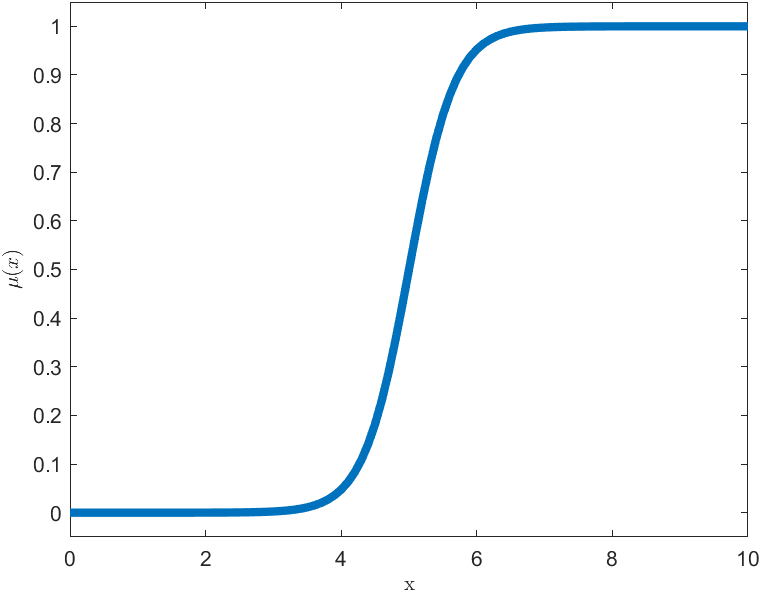
Funkcja sigmoidalna

$$

\mu(x,a,b) = \frac{1}{1+  e^{-a(x-b)}}

$$