Podręcznik

3. Stosy i kolejki jako elementarne struktury danych

Kolejka (ang. queue)jest bardzo prostą i intuicyjną strukturą, która odpowiada wielu sytuacjom z życia codziennego. Wyobraźcie sobie np. kolejkę do okienka w urzędzie, kolejkę do kasy w sklepie czy też kolejkę pasażerów wchodzących do autobusu. Zasada jest zawsze taka sama: osoby (elementy) dołączają na końcu kolejki, a obsługa odbywa się od początku.

Pod względem technicznym kolejka to struktura dynamiczna lub statyczna, która udostępnia dwa podstawowe operatory:

enqueue (dodanie elementu do kolejki, zwykle na końcu),
dequeue (usunięcie elementu z kolejki, czyli wyjęcie pierwszego elementu).

Czasami udostępnia się też operator peek (podgląd pierwszego elementu bez usuwania go), dzięki czemu można sprawdzić, jaki element będzie obsłużony jako następny.

Struktura FIFO znajduje zastosowanie w bardzo wielu algorytmach i systemach informatycznych. Przykładowo:

kolejki zadań w systemach operacyjnych,
buforowanie danych w transmisji sieciowej,
implementacja algorytmu przeszukiwania grafu (ang. BFS — Breadth-First Search),
obsługa zdarzeń w grach komputerowych lub w interfejsach użytkownika.

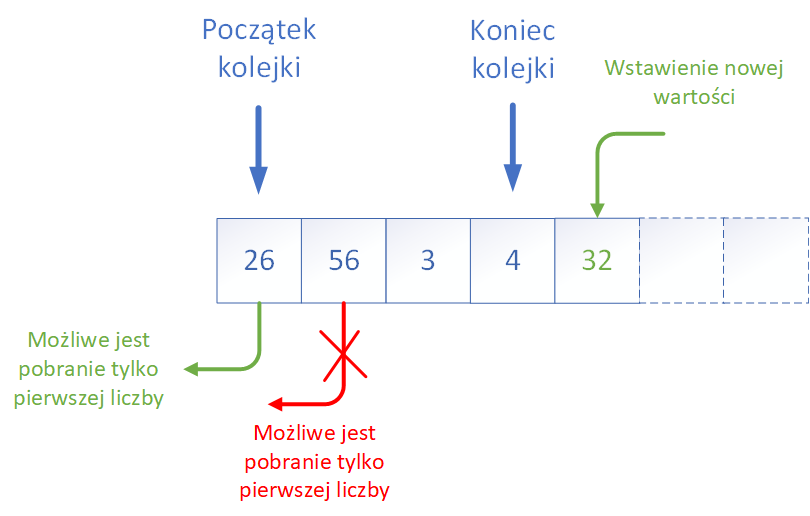
Na rysunku przedstawiono sposób umieszczenia elementów w klasycznej kolejce oraz ich pobierania. Pobieranie elementów możliwe jest tylko z początku kolejki, natomiast nie ma możliwości pobierania z innych indeksów struktury danych.

Kolejkę można zaimplementować na wiele sposobów:

jako tablicę z dwoma indeksami (początku i końca),
jako listę jednokierunkową, gdzie nowe elementy dodawane są na końcu, a usuwane z początku,
z wykorzystaniem gotowych struktur dostępnych w językach wysokiego poziomu (np. queue w C++, Queue w Javie czy collections.deque w Pythonie).

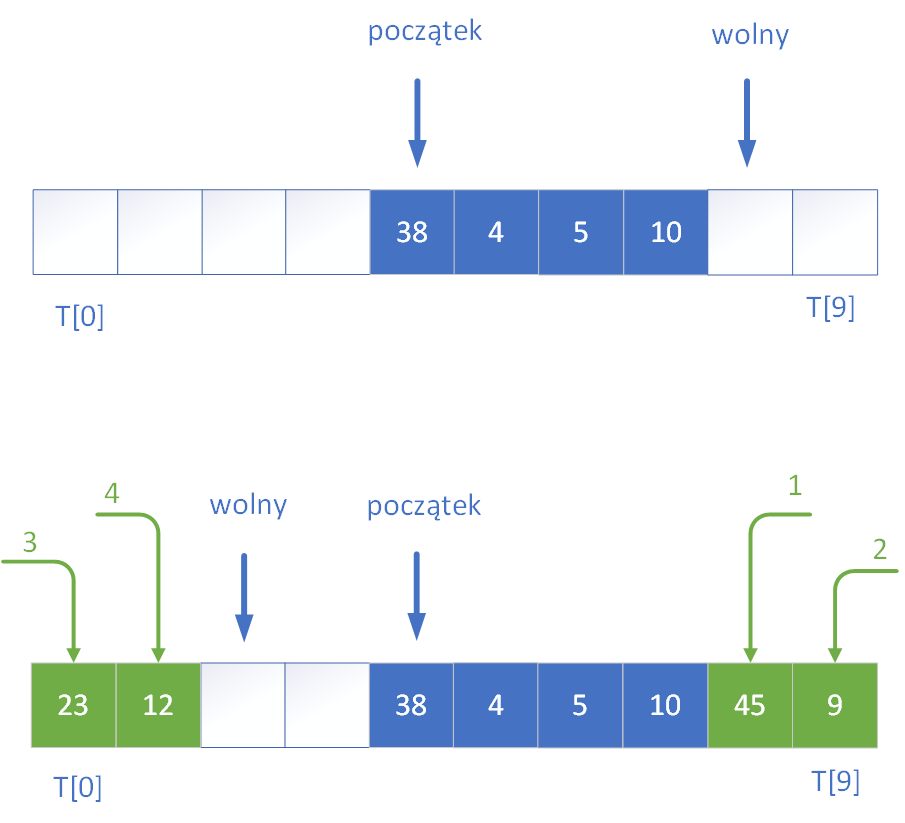
W podręczniku przedstawimy implementację w postaci tablicy z dwoma indeksami (początku i końca). Dodatkowo będzie to implementacja bufora cyklicznego. Jest to bardzo popularne podejście w tego typu rozwiązaniach. Ideę bufora cyklicznego wyjaśnia szczegółowo poniższy rysunek. Rysunek pokazuje operację wstawiania do bufora cyklicznego czterech wartości. Numerami pokazana jest kolejność zamieszczania poszczególnych elementów w tablicy. W tablicy o rozmiarze n można zaimplementować kolejkę o rozmiarze n-1. Kolejka jest pusta jeżeli początek=wolny oraz pełna gdy początek=wolny+1.

Kolejny przykład rysunkowy demonstruje w jaki sposób pobrać elementy z kolejki. W przykładzie pobierane są dwie wartości z kolejki.

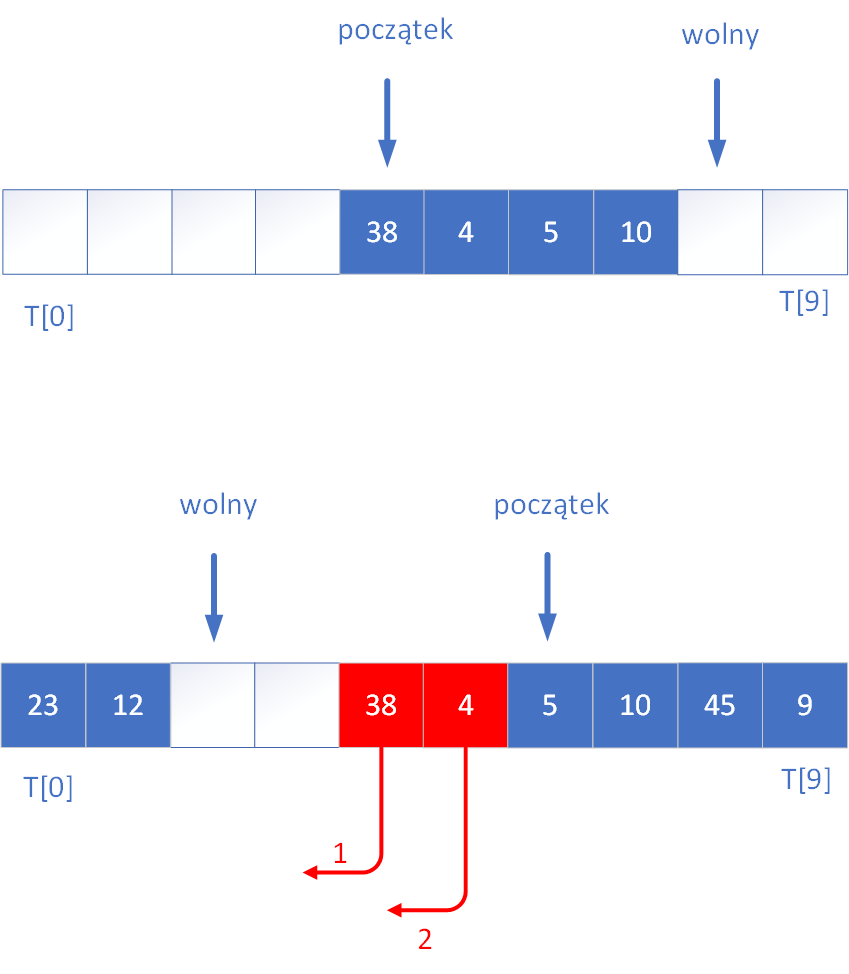
Zauważcie tylko przyglądając się rysunkowi, że w pełniącej rolę bufora cyklicznego tablicy, która ma miejsce na n elementów, zawsze jedno miejsce pozostaje nie wykorzystane, dzięki czemu możemy odróżnić stan, kiedy kolejka jest pusta (indeksy poczatek i wolny są sobie równe) od stanu jej zapełnienia (poczatek=wolny+1).

Struktura kolejki jest wykorzystywana w wielu algorytmach komputerowych, a jednym z najważniejszych zastosowań jest kolejkowanie procesów oczekujących na wykonanie na procesorze komputera.

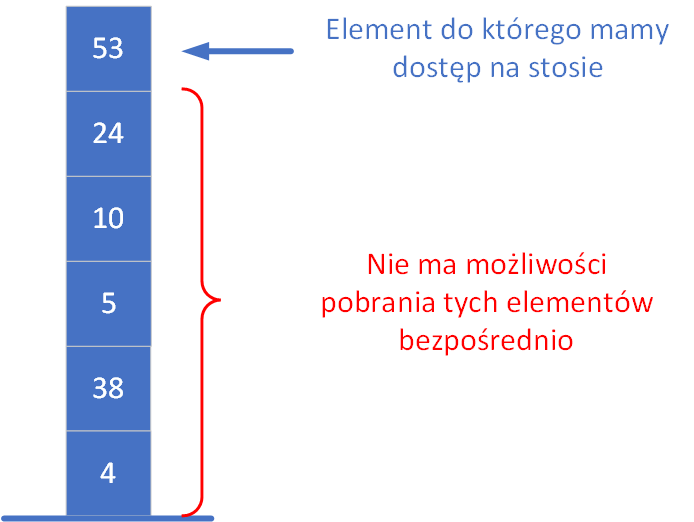
Stos (ang. stack) jest jedną z najważniejszych struktur danych używanych w algorytmach komputerowych. Podstawowe cechy można zawrzeć w stwierdzeniu "ostatni wchodzi - pierwszy wychodzi", czyli w skrócie LIFO (Last In – First Out).

Obsługa stosu polega na tym, że dostęp do danych możliwy jest wyłącznie z jednej strony – od góry stosu. Można to porównać do układania kart do gry jedna na drugiej. Nowe karty zawsze kładziemy na wierzchu, a jeśli chcemy sięgnąć po kartę znajdującą się niżej, musimy najpierw zdjąć wszystkie leżące nad nią. Aby dotrzeć do pierwszej z położonych kart, konieczne jest usunięcie kolejnych – aż odsłonimy tę, której szukamy. Oznacza to, że elementy są zdejmowane w odwrotnej kolejności niż zostały dodane.

Przy implementacji stosu zazwyczaj definiuje się dwie podstawowe operacje, które umożliwiają jego obsługę. Najczęściej nazywa się je:

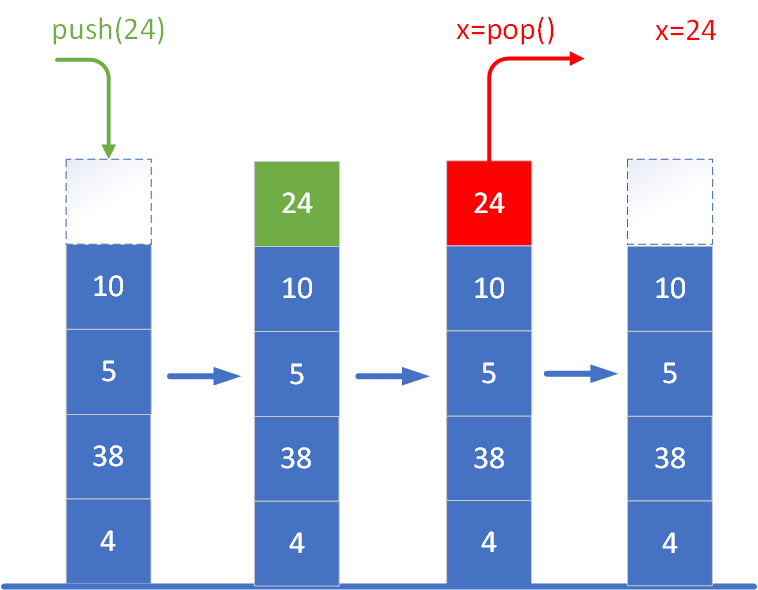
push(x) – dodaje element x na szczyt stosu. To tak, jakby położyć nową kartę na samą górę stosu. Operacja ta zwiększa rozmiar stosu o jeden i sprawia, że nowo dodany element staje się pierwszym do usunięcia.
pop() – usuwa element znajdujący się aktualnie na szczycie stosu i zwykle go zwraca. Jeśli stos jest pusty, próba wykonania tej operacji może zakończyć się błędem (w zależności od implementacji), ponieważ nie ma elementu do usunięcia.

Te dwie operacje w pełni definiują zachowanie stosu zgodnie z zasadą LIFO (Last In, First Out), co oznacza, że ostatni dodany element jest usuwany jako pierwszy. Na rysunku poniżej przedstawiono podstawowe operacje na stosie.

W praktycznych implementacjach stosu (np. w językach programowania takich jak Python, Java, C++) często dodaje się również dodatkowe metody pomocnicze, takie jak:

peek() lub top() – pozwala podejrzeć element znajdujący się na szczycie stosu bez jego usuwania,
isEmpty() – sprawdza, czy stos jest pusty,
size() – zwraca liczbę elementów znajdujących się aktualnie na stosie.

Stos jest jedną z podstawowych struktur danych i znajduje zastosowanie m.in. w analizie wyrażeń arytmetycznych, wywoływaniu funkcji (stos wywołań), przetwarzaniu nawiasów, czy przy realizacji algorytmów rekurencyjnych.

Stos jest taką strukturą danych, która skutecznie pomaga zwiększyć efektywność niektórych algorytmów. Pokażemy to na przykładzie obliczeń związanych z Odwrotną Notacją Polską (ONP). Odwrotna Notacja Polska (ONP), nazywana również notacją postfiksową, to sposób zapisu wyrażeń arytmetycznych, w którym operatory występują po operandach, a nie pomiędzy nimi – jak ma to miejsce w tradycyjnym zapisie infiksowym. Przykładowo, wyrażenie „2 + 3” w ONP przyjmuje postać „2 3 +”. Choć taki zapis może początkowo wydawać się mniej intuicyjny, niesie ze sobą liczne korzyści, szczególnie w kontekście przetwarzania wyrażeń przez komputer. Jedną z najważniejszych cech ONP jest to, że nie wymaga ona stosowania nawiasów. Kolejność wykonywania operacji wynika wprost z kolejności, w jakiej występują operatory i operandy. Dzięki temu unika się niejednoznaczności i konieczności stosowania dodatkowych zasad pierwszeństwa działań. W wyrażeniach ONP zawsze operujemy na dwóch ostatnich liczbach umieszczonych wcześniej w ciągu.

Wyrażenia zapisane w ONP są wyjątkowo łatwe do przetwarzania algorytmicznego, zwłaszcza przy użyciu stosu. Podczas obliczeń elementy (liczby) są kolejno umieszczane na stosie. Kiedy napotkamy operator, zdejmujemy ze stosu dwa ostatnie elementy, wykonujemy odpowiednią operację i wynik odkładamy z powrotem na stos. Proces ten powtarza się aż do momentu przetworzenia całego wyrażenia, a końcowy wynik znajduje się na szczycie stosu jako jedyny pozostały element.

Słowny opis algorytmu przetwarzania jednego znaku pobranego z wejścia można w skrócie przedstawić tak:

jeżeli znak odczytany z wejścia jest cyfrą, dodaj go do łańcucha wyjściowego
jeżeli odczytany znak jest operatorem, to:
- jeśli na szczycie stosu znajduje się operator o wyższym lub równym priorytecie względem priorytetu operatora odczytanego z wejścia, zdejmij ten "silniejszy" operator ze stosu i dodaj do kolejki wyjściowej - powtarzaj to aż do momentu, gdy na (nowym) szczycie stosu znajdzie się operator o niższym priorytecie, wtedy:
- odłóż odczytany z wejścia operator na stos – tak samo postąp, gdy stos będzie pusty (od razu bądź też po zdjęciu ze stosu innych operatorów)
jeżeli odczytany znak jest lewym nawiasem, to odłóż go na stos, natomiast
jeżeli oczytany znak jest prawym nawiasem, to zdejmuj po kolei operatory ze stosu i przekazuj na wyjście aż do momentu, gdy na szczycie stosu znajdzie się lewy nawias – wtedy zdejmij ten nawias ze stosu.

Algorytm przetwarzania zapisu infiksowego na ONP kończy się, jeżeli wszystkie znaki z wejścia zostały odczytane i przetworzone. W sytuacji, gdy stos jest niepusty, należy przekazać pozostałe znaki operatorów na wyjście.

Poniżej przedstawiono tabelę priorytetów dla czterech podstawowych operandów arytmetycznych.

Najlepiej zademonstrować działanie algorytmu na prostym przykładzie. Jako ciąg wejściowy wprowadzamy wyrażenie: (4+6)*(8-3)/2.

Symulacja konwersji na ONP

Wyrażenie: (4 + 6) * (8 - 3) / 2

Dla każdego tokena w wyrażeniu:
  jeśli to liczba → dodaj do wyjścia
  jeśli to '(' → połóż na stos
  jeśli to ')' → zdejmuj ze stosu do '('
  jeśli to operator → zdejmuj silniejsze operatory ze stosu, potem połóż
Po zakończeniu → zdejmij wszystko ze stosu

Stos operatorów:

Wyjście (ONP):

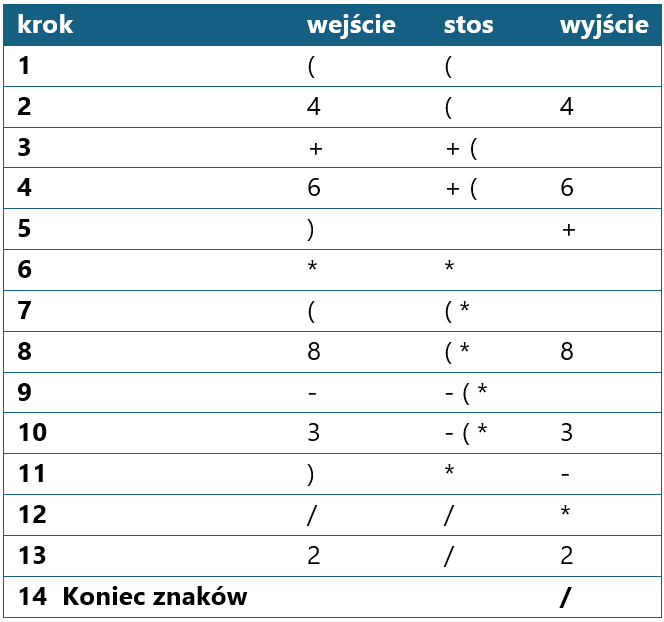
Przekład można przedsatwić także w formie tabelarycznej, która pokazuje wszystkie kroki działania algorytmu.

Ciąg znaków wyjściowych: 4 6 + 8 3 - * 2 /

Podczas implementacji należy pamiętać o tym, by po dopisaniu do łańcucha wyjściowego operatora bądź też ostatniej cyfry liczby umieścić znak biały ' ', dzięki któremu unikniemy „złączenia” się dwóch liczb w jedną (w naszym przykładzie musimy zapisać „4 6 + 8 3 - * 2 /”, a nie „46+83-*2/”).

Wiemy już, jak przetworzyć zapis w notacji konwencjonalnej do postaci ONP. Za chwilę dowiemy się, jak za pomocą stosu - tym razem liczbowego - w szybki sposób obliczać wartość wyrażenia przedstawionego właśnie w zapisie postfiksowym.

Okazuje się, że taki algorytm może być naprawdę prosty w zapisie, a przy tym efektywny. Tym razem jest nam potrzebny ciąg wejściowy będący zapisem wyrażenia w notacji ONP oraz stos pozwalający na przechowywanie liczb. Wynik wyrażenia jest zdejmowany ze stosu na samym końcu.

Kroki algorytmu są następujące:

jeżeli znak odczytany z wejścia jest cyfrą, to pobieraj kolejne znaki budując z nich liczbę, aż natrafisz na znak nie będący cyfrą - wtedy otrzymaną liczbę odłóż na stos
jeżeli znak jest operatorem, to
- zdejmij ze stosu dwie liczby (pierwszą zdjętą niech będzie x, drugą y)
- oblicz wartość wyrażenia y operator x
- odłóż obliczoną wartość na stos
gdy już skończą się znaki w ciągu wejściowym, zdejmij ze stosu końcowy wynik.

Symulacja obliczania wartości ONP

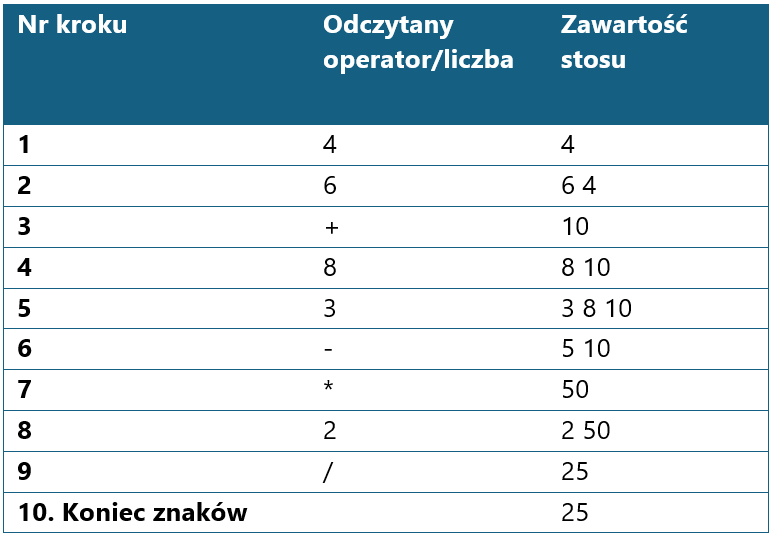
Wyrażenie ONP: 4 6 + 8 3 - * 2 /

Dla każdego tokena w wyrażeniu:
  jeśli to liczba → odłóż na stos
  jeśli to operator:
    zdejmij x i y ze stosu
    oblicz y operator x i odłóż wynik na stos
Na końcu zdejmij wynik ze stosu

Stos liczbowy:

Aktualny token:

Analogicznie jak poprzednio poszczególne kroki algorytmu można także przedstawić w formie tabelarycznej: