Podręcznik

5. Złożoność obliczeniowa

Zagadnienia złożoności obliczeniowej algorytmów stanowią fundament matematycznej analizy efektywności aplikacji komputerowych. Stanowią one istotny punkt wyjścia w nauce algorytmiki. Umożliwiają ocenę jakości danego rozwiązania niezależnie od konkretnego sprzętu, języka programowania czy implementacji. Głównym celem wyznaczania złożoności obliczeniowej jest efektywność działania algorytmu rozumiana jako ilość zasobów niezbędnych do jego wykonania, w szczególności czasu oraz pamięci. Wprowadzenie tych pojęć pozwala sformułować precyzyjne miary porównawcze dla różnych metod rozwiązania tego samego problemu.

Z matematycznego punktu widzenia, złożoność czasowa i pamięciowa algorytmu jest wyrażana jako funkcja zmiennej naturalnej $n$n, która opisuje rozmiar danych wejściowych. Interesuje nas przy tym przede wszystkim asymptotyczne zachowanie tej funkcji, czyli jak rośnie liczba operacji lub potrzebna pamięć, gdy $n\to \mathrm{\infty }$. Do zapisu tego wzrostu stosuje się tzw. notację dużego O – oznaczaną jako $O(f(n))$, gdzie $f(n)$ jest funkcją ograniczającą wzrost złożoności od góry. Przykładowo, jeśli algorytm wykonuje maksymalnie $3n^2+2n+1$3 operacji, to jego złożoność asymptotyczna to $O(n^2)$, ponieważ składnik kwadratowy dominuje dla dużych wartości $n$.

W praktyce często porównujemy algorytmy poprzez analizę ich złożoności w różnych przypadkach: najgorszym, średnim i najlepszym. Taka analiza pozwala przewidywać zachowanie algorytmu nie tylko w idealnych, ale i w rzeczywistych warunkach. Na przykład wyszukiwanie liniowe ma złożoność $O(n)$ w najgorszym przypadku, ale wyszukiwanie binarne – już tylko $O(\log n)$, co wprowadza jakościową różnicę przy dużych zbiorach danych.

W algorytmice nie chodzi jednak wyłącznie o zminimalizowanie złożoności. Równie istotna jest czytelność, poprawność i łatwość implementacji algorytmu. Czasem prostszy, choć teoretycznie wolniejszy algorytm, może okazać się lepszym wyborem, szczególnie w sytuacjach, gdy dane wejściowe mają niewielki rozmiar lub gdy istotna jest szybkość implementacji rozwiązania. Ważne jest także, by algorytm spełniał warunek stopu, czyli kończył działanie dla danych poprawnych w skończonym czasie – co formalnie oznacza, że musi on być funkcją totalną.

Wprowadzenie pojęcia złożoności pozwala zidentyfikować i poprawić nieefektywne fragmenty algorytmów. Na przykład, odczytanie głównej przekątnej macierzy $n\times n$ można wykonać w czasie $O(n)$, używając jednej pętli. Jednak początkujący mogą nieświadomie zastosować algorytm złożony z dwóch pętli z warunkiem $i==j$, co prowadzi do złożoności $O(n^2)$ – mimo że problem da się rozwiązać znacznie szybciej. W tym miejscu ujawnia się praktyczna wartość analizy złożoności: pozwala ona uniknąć niewidocznych gołym okiem nieefektywności.

Ostatecznie, złożoność obliczeniowa to narzędzie matematyczne, które służy nie tylko do porównywania algorytmów, lecz również do ich projektowania i optymalizacji. Dzięki niej jesteśmy w stanie zrozumieć granice obliczalności problemów, klasyfikować zadania według trudności (np. klasy P, NP, NP-zupełne) oraz podejmować świadome decyzje projektowe. Choć złożoność pamięciowa jest dziś mniej krytyczna z racji dużej dostępności RAM, nadal pozostaje istotna np. w systemach wbudowanych lub przy pracy na wielkich zbiorach danych. Jednak to złożoność czasowa pozostaje najczęściej analizowanym i najważniejszym aspektem efektywności algorytmicznej.

Notacja dużego O (czyli tzw. big-O notation) to kluczowe narzędzie matematyczne służące do opisu zachowania algorytmu przy dużych danych wejściowych. Zamiast analizować dokładną liczbę operacji, jakie wykonuje program, interesuje nas ogólny trend wzrostu tej liczby w zależności od rozmiaru wejścia. Umożliwia to ocenę i porównanie efektywności algorytmów niezależnie od konkretnej maszyny czy języka programowania.

Formalnie, mówimy, że funkcja $f(n)$ ma złożoność $O(g(n))$, jeśli istnieją stałe $c>0$ oraz $N\ge 0$, takie że dla wszystkich $n\ge N$ zachodzi nierówność:

$$f(n)\le c\cdot g(n)$$

Oznacza to, że dla dużych $n$n, funkcja $f(n)$ jest ograniczona z góry przez pewną wielokrotność funkcji $g(n)$. Intuicyjnie: nie rośnie szybciej niż $g(n)$, pomnożone przez jakąś stałą. Taka definicja opisuje asymptotyczny kres górny, czyli zachowanie algorytmu „na dłuższą metę” – ignorując drobne różnice dla małych wartości $n$n, a skupiając się na tym, jak zachowuje się on, gdy rozmiar danych rośnie do nieskończoności.

Na przykład, jeśli algorytm wykonuje $f(n)=3n^2+5n+7$ operacji, to mówi się, że ma on złożoność $O(n^2)$. Pomijamy tutaj współczynniki stałe (takie jak 3 czy 5), ponieważ interesuje nas jedynie kształt wzrostu funkcji. Z tego względu funkcje takie jak $10n^2+100n$ i $n^2\mathrm{}\mathrm{}$ również uznaje się za rzędu $O(n^2)$O( n2 ), mimo że ich wartości dla konkretnych $n$n mogą być różne.

Często spotykane klasy funkcji używanych w notacji dużego O to:

• $O(1)$ – stała złożoność (niezależna od rozmiaru wejścia),

• $O(\log n)$ – logarytmiczna (np. przeszukiwanie binarne),

• $O(n)$ – liniowa (np. przeglądanie tablicy),

• $O(n\log n)$ – liniowo-logarytmiczna (np. szybkie algorytmy sortowania),

• $O(n^2)$, $O(n^3)$– złożoności wielomianowe (np. sortowanie bąbelkowe, algorytmy dynamiczne),

• $O(2^n)$, $O(n!)$ – złożoności wykładnicze i silniowe (dla problemów trudnych obliczeniowo, np. w teorii grafów, NP-trudne zadania).

Z wykresu funkcji takich jak $\log n$, $n$, $n\log n$n, $n^2$, $2^n$ widać, jak drastycznie różni się ich tempo wzrostu. Funkcja $O(n\log n)$ – charakterystyczna dla szybkich algorytmów sortowania – leży pomiędzy funkcją liniową a kwadratową, ale rośnie znacznie wolniej niż ta druga. Tymczasem $O(2^n)$ wznosi się tak stromo, że dla nawet umiarkowanie dużych danych staje się praktycznie nieużyteczna.

W praktyce, kiedy szukamy najlepszego algorytmu, dążymy do tego, by jego złożoność była jak najmniejsza – np. zamiast algorytmu $O(n^2)$, warto znaleźć taki, który działa w $O(n\log n)$, a idealnie – w $O(n)$, jeśli to możliwe. Złożoność w notacji dużego O pozwala więc nie tylko na efektywne porównywanie algorytmów, ale także stanowi fundament teorii obliczalności i klasyfikacji problemów pod kątem ich trudności obliczeniowej.

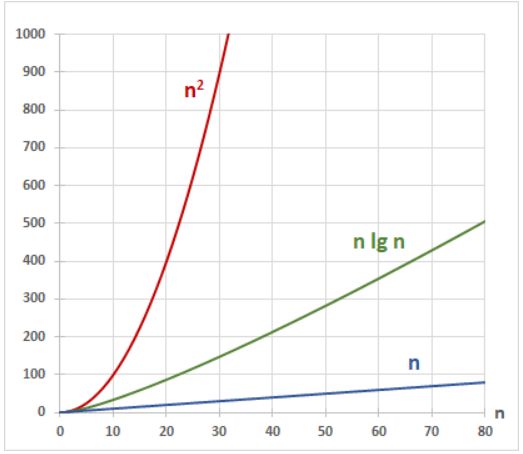
Na wykresie pokazano złożoność obliczeniową w zależności od liczby danych.