7. Problem skoczka szachowego

Problem skoczka szachowego (ang. Knight's Tour Problem) to klasyczny problem kombinatoryczny z teorii grafów i algorytmiki, który polega na znalezieniu takiej sekwencji ruchów skoczka szachowego, aby odwiedził on każde pole szachownicy dokładnie raz. Skoczek porusza się zgodnie z regułami gry w szachy – wykonuje ruch w kształcie litery „L”, czyli dwa pola w jednym kierunku (poziomo lub pionowo), a następnie jedno pole prostopadle. Celem jest zaplanowanie takiej trasy, która obejmuje wszystkie pola na szachownicy bez powtórzeń, czyli tzw. pełnej trasy.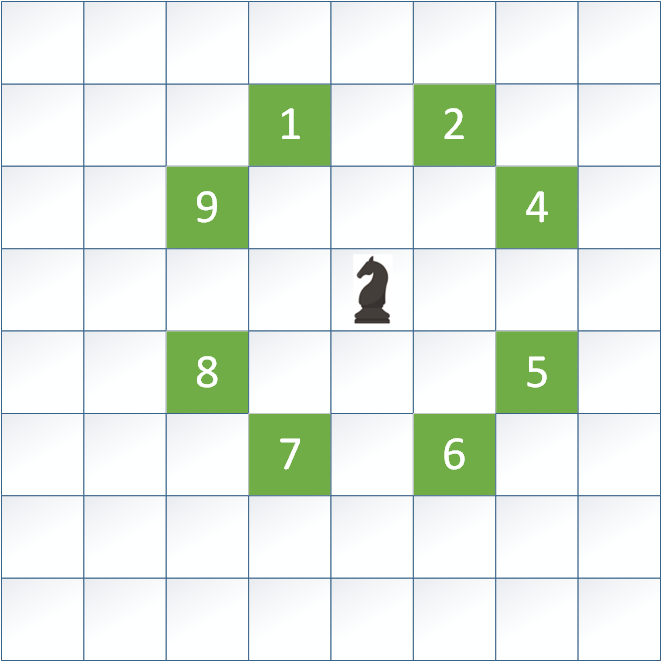


Problemem poruszania się konika po szachownicy zajmowało się w przeciągu ostatnich dwustu lat bardzo wielu wybitnych matematyków i naukowców. Dzisiaj wiemy na przykład, że w przypadku szachownicy o rozmiarze m x n, gdzie min(m,n) >= 5, zawsze istnieje ścieżka skoczka przechodząca przez wszystkie pola dokładnie raz. Dla naszego przypadku 8 istnieje pewność, że możliwe jest znalezienie rozwiązania. 

Poniżej przedstawiono kod umożliwiający rozwiązanie problemu skoczka przy pomocy algorytmu z powrotami (ang. backtracking). 

#include <iostream>
#include <iomanip>

const int N = 8;  // rozmiar szachownicy

// Możliwe ruchy skoczka (x, y)
int dx[8] = { 2, 1, -1, -2, -2, -1, 1, 2 };
int dy[8] = { 1, 2, 2, 1, -1, -2, -2, -1 };

// Funkcja do weryfikacji czy ruch jest możliwy
bool isSafe(int x, int y, int board[N][N]) {
    return (x >= 0 && x < N &&
            y >= 0 && y < N &&
            board[x][y] == -1);
}

// Funkcja do rekurencyjnego rozwiązania problemu skoczka
bool solveKnightTour(int x, int y, int moveCount, int board[N][N]) {
    if (moveCount == N * N) return true;

    for (int i = 0; i < 8; i++) {
        int nextX = x + dx[i];
        int nextY = y + dy[i];

        if (isSafe(nextX, nextY, board)) {
            board[nextX][nextY] = moveCount;
            if (solveKnightTour(nextX, nextY, moveCount + 1, board))
                return true;
            else
                board[nextX][nextY] = -1;
        }
    }
    return false;
}

// Funkcja uruchamiająca algorytm
void startKnightTour() {
    int board[N][N];

    // Inicjalizacja planszy
    for (int i = 0; i < N; i++)
        for (int j = 0; j < N; j++)
            board[i][j] = -1;

    int startX = 0, startY = 0; // punkt startowy
    board[startX][startY] = 0;  // pierwszy ruch

    if (solveKnightTour(startX, startY, 1, board)) {
        // Wyświetlenie rozwiązania
        for (int i = 0; i < N; i++) {
            for (int j = 0; j < N; j++)
                std::cout << std::setw(2) << board[i][j] << " ";
            std::cout << std::endl;
        }
    } else {
        std::cout << "Brak rozwiązania." << std::endl;
    }
}

int main() {
    startKnightTour();
    return 0;
}

Za pomocą kodu można samodzielnie sprawdzić działanie algorytmu dla dowolnej wielkości planszy oraz dowolnego punktu startowego. Poniżej pokazano kolejne kroki algorytmu dla przykładowego punktu startowego znajdującego się w górnym lewym rogu szachownicy.

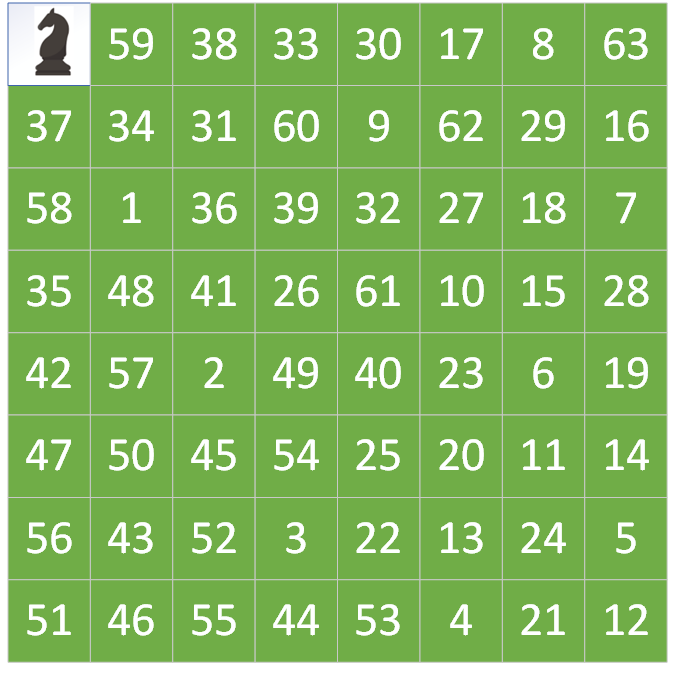
Można zaobserwować analizując poszczególne ruchy, że każde pole zostało odwiedzone tylko raz oraz że zostały odwiedzone wszystkie pola na szachownicy.

Poniżej macie symulator za pomocą którego możecie symulować działanie algorytmu z powrotami dla dowolnego punktu startowego oraz wielkości planszy <5;8>. Po każdym uruchomieniu za pomocą Start należy użyć Stop, aby było możliwe ponowne uruchomienie symulatora.

W symulatorze zaimplementowano także heurystykę Warnsdorffa w celu przyspieszenia obliczeń. Możecie sprawdzić jak szybko działa algorytm z powrtotami, a jak działa algorytm w oparciu o heurystykę. Heurystyka Warnsdorffa to efektywna metoda przyspieszająca rozwiązywanie problemu skoczka szachowego. Została opracowana w XIX wieku przez niemieckiego matematyka H. C. Warnsdorffa i do dziś stanowi jedną z najskuteczniejszych strategii dla tego typu zadań. Jej podstawową ideą jest wybieranie w każdym kroku takiego ruchu skoczka, który prowadzi do pola z najmniejszą liczbą dalszych dostępnych ruchów. Dzięki temu unika się sytuacji, w których skoczek mógłby zablokować sobie drogę i nie być w stanie odwiedzić wszystkich pól planszy. Zamiast przeszukiwać wiele potencjalnych ścieżek, jak robi to klasyczny algorytm z powrotami, heurystyka Warnsdorffa kieruje się prostą obserwacją: pola, z których można wykonać mało ruchów, są najbardziej „ryzykowne” i powinny zostać odwiedzone jak najwcześniej. Strategia ta pozwala więc skoczkowi poruszać się w sposób bardziej rozważny i minimalizuje ryzyko utknięcia w martwym punkcie planszy. W praktyce oznacza to, że z dostępnych w danym momencie opcji ruchu wybierana jest ta, która daje najmniejszą swobodę w kolejnych turach. W przypadku remisu – gdy kilka pól ma tę samą liczbę kontynuacji – można wybierać losowo lub według ustalonego porządku. Zaletą heurystyki Warnsdorffa jest jej bardzo wysoka wydajność. Pozwala rozwiązać problem skoczka niemal natychmiastowo nawet na planszach dużych rozmiarów, takich jak klasyczna szachownica 8×8. W wielu przypadkach prowadzi do poprawnego rozwiązania bez potrzeby cofania się i analizowania alternatywnych ścieżek. Nie gwarantuje jednak znalezienia rozwiązania w każdym możliwym układzie – jako heurystyka, nie zapewnia pełnej niezawodności. Może się zdarzyć, że dla nietypowego punktu startowego lub specyficznego rozmiaru planszy nie znajdzie trasy, choć taka istnieje.