Podręcznik

3. Sortowanie przez scalanie

Sortowanie przez scalanie (ang. MergeSort) to klasyczny algorytm oparty na metodzie „dziel i zwyciężaj”. Charakteryzuje się bardzo dobrą złożonością czasową O(n log n) niezależnie od charakteru danych wejściowych, dzięki czemu znajduje zastosowanie w sytuacjach, gdzie wymagana jest przewidywalność wydajności. Sortowanie przez scalanie działa stabilnie i nieprzerwanie oraz odgrywa ważną rolę w implementacjach systemowych oraz bibliotek standardowych wielu języków programowania. Algorytm ten opiera się na dzieleniu tablicy na coraz mniejsze części, aż do momentu, gdy każda z nich zawiera tylko jeden element. Taka jednoelementowa tablica jest już posortowana, więc może być poddana scaleniu z inną. Scalanie dwóch posortowanych tablic polega na porównywaniu ich elementów i dokładaniu ich w odpowiedniej kolejności do nowej tablicy wynikowej. Ten etap gwarantuje, że z dwóch uporządkowanych części powstaje nowa, również uporządkowana całość. Poniżej na rysunku przedstawiono działanie algorytmu przez scalanie.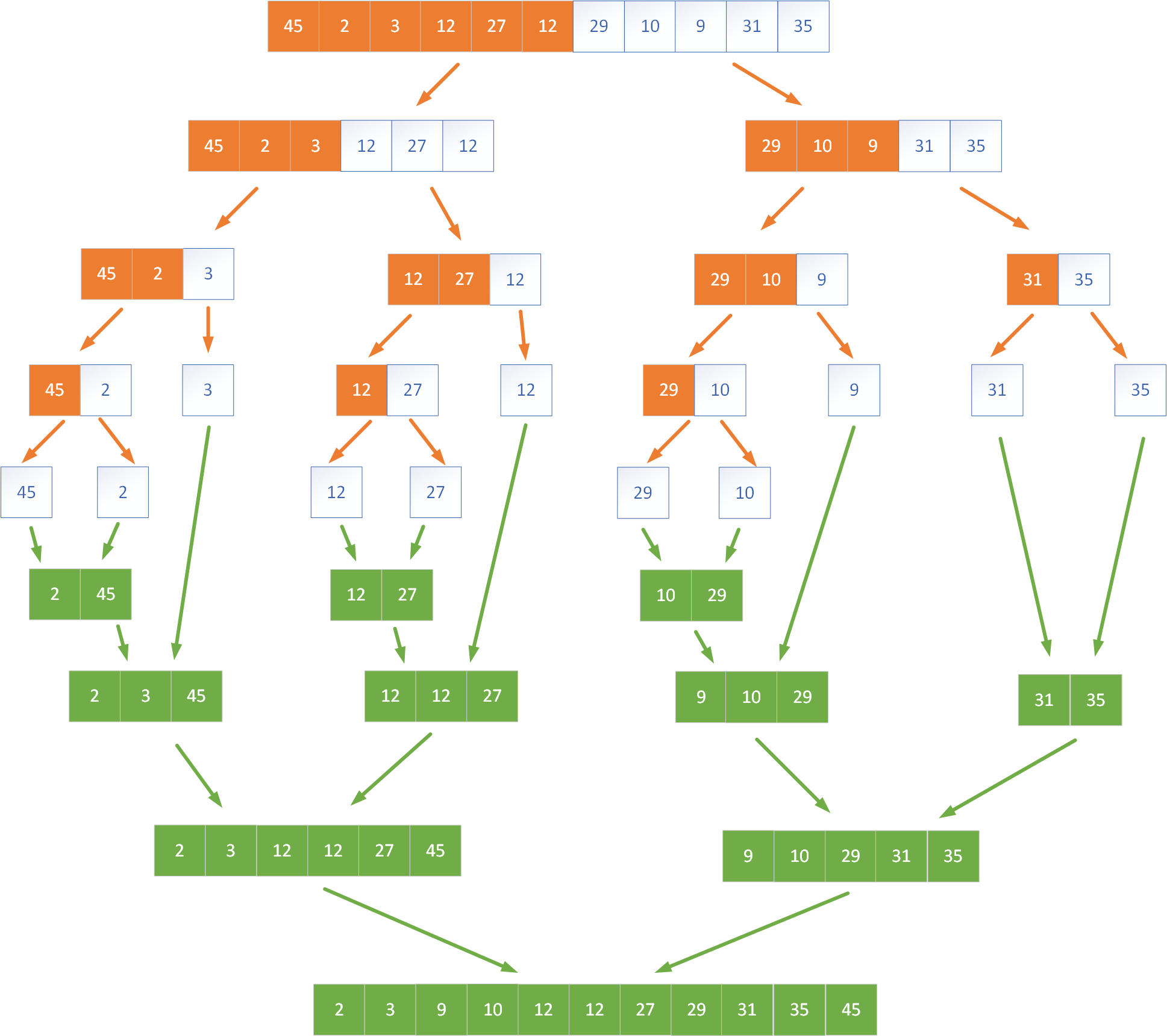


Scalenie podtablic odbywa się poprzez użycie funkcji, która w implementacjach najczęściej nosi nazwę Merge. Jej zadaniem jest przenoszenie danych z dwóch posortowanych podtablic do tablicy w taki sposób, aby otrzymać ciąg danych posortowanych. Metoda Merge tworzy pomocnice tablice, do których przepisywane są dwie podtablice, które należy scalić. Do źródłowej tablicy T przepisywane są z powrotem elementy tablic L i P – za każdym razem porównujemy ze sobą 2 najmniejsze elementy L i P, które jeszcze nie zostały przepisane do T. Wybieramy mniejszego z nich, którego należy umieścić w „dużej” tablicy, a następnie procedurę porównywania i przekazywania elementów prowadzimy do momentu „wyczerpania się” tablic L oraz P. Aby zmusić algorytm do wykorzystania wszystkich elementów ze wspomnianych tablic, używamy wartowników o dużej wartości w ostatnich komórkach tablic – dzięki temu, gdy z jednej z tablic zostaną już przepisane wszystkie elementy, nastąpi potem przepisanie reszty pozostałych elementów w drugiej tablicy do tablicy T. Poniżej przedstawiono schemat działania metody Merge w algorytmie.

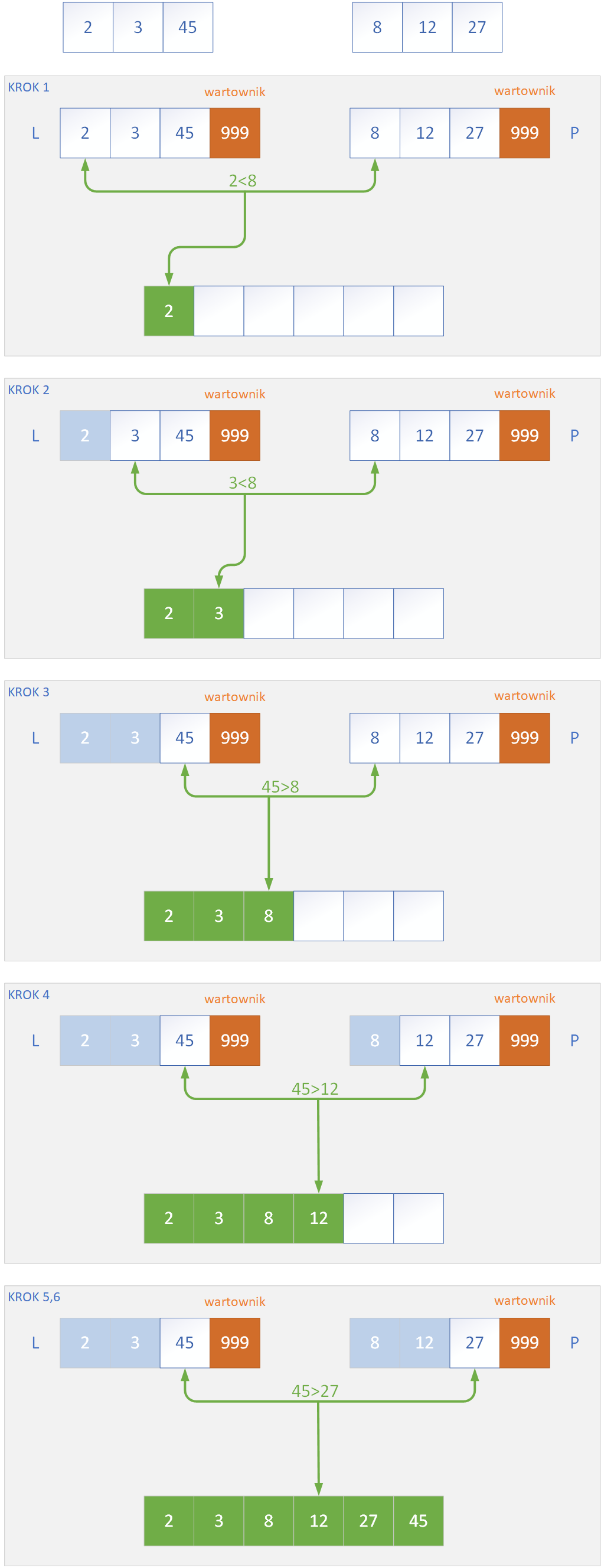
 Poniżej przedsatwiono kod w C++ do realizacji algorytmu sortowania przez scalanie.

#include <iostream>
#include <vector>
using namespace std;

void merge(vector<int>& T, int left, int mid, int right) {
    int n1 = mid - left + 1;
    int n2 = right - mid;
    vector<int> L(n1), R(n2);

    for (int i = 0; i < n1; i++)
        L[i] = T[left + i];
    for (int j = 0; j < n2; j++)
        R[j] = T[mid + 1 + j];

    int i = 0, j = 0, k = left;
    while (i < n1 && j < n2) {
        if (L[i] <= R[j]) {
            T[k] = L[i];
            i++;
        } else {
            T[k] = R[j];
            j++;
        }
        k++;
    }

    while (i < n1) {
        T[k] = L[i];
        i++;
        k++;
    }
    while (j < n2) {
        T[k] = R[j];
        j++;
        k++;
    }
}

void mergeSort(vector<int>& T, int left, int right) {
    if (left < right) {
        int mid = left + (right - left) / 2;
        mergeSort(T, left, mid);
        mergeSort(T, mid + 1, right);
        merge(T, left, mid, right);
    }
}

void printArray(const vector<int>& T) {
    for (int x : T)
        cout << x << " ";
    cout << endl;
}

int main() {
    vector<int> T = { 38, 27, 43, 3, 9, 82, 10 };

    cout << "Przed sortowaniem: ";
    printArray(T);

    mergeSort(T, 0, T.size() - 1);

    cout << "Po sortowaniu: ";
    printArray(T);

    return 0;
}