Podręcznik
3. Algorytm Dijkstry
Algorytm Dijkstry to jeden z najbardziej znanych i najczęściej używanych algorytmów grafowych. Służy do znajdowania najkrótszych ścieżek od jednego wierzchołka (źródła) do wszystkich innych wierzchołków w grafie o nieujemnych wagach krawędzi. Został opracowany przez holenderskiego informatyka Edsgera Dijkstrę w 1956 roku. Jest podstawą wielu zastosowań, m.in. w systemach GPS, analizie sieci, komunikacji i teorii tras.Metoda Dijkstry polega na wprowadzeniu podziału zbioru wierzchołków grafu na trzy zbiory:
- zbiór Q, w którym znajdują się wierzchołki, do których „dotarł” już algorytm, ale nie możemy jeszcze określić, czy znaleziono do nich najkrótszą ścieżkę ze źródła
- zbiór S, w którym znajdują się wierzchołki (węzły) grafu o już ustalonej najkrótszej ścieżce ze źródła, dalej nie będą już rozpatrywane w algorytmie
- pozostałe węzły, czyli zbiór V- Q – S, gdzie V jest zbiorem wszystkich wierzchołków grafu G = (V, E)
Warto nadmienić, że częściej spotykana wersja algorytmu Dijkstry zakłada, że do zbioru Q trafiają „od razu” wszystkie węzły grafu G, a następnie są po kolei pobierane pojedynczo węzły, które trafiają do zbioru S.
Idea omawianego algorytmu jest następująca. Rozpoczynamy od dodania węzła źródłowego r do zbioru Q. Następnie rozpoczynamy cykliczne wykonywanie ciągu operacji, na który składa się:
- wybranie ze zbioru Q wierzchołka o znanej najmniejszej odległości od źródła (nazwijmy go Vi)
- dodanie powyższego węzła do zbioru S
- przejrzenie wszystkich sąsiednich węzłów wierzchołka Vi, które nie należą do zbioru S – następnie jest sprawdzane, czy droga ze źródła do sąsiada (oznaczmy ten węzeł jako Vj) prowadząca przez węzeł Vi jest krótsza niż najkrótsza ścieżka znana do tej pory, jeśli tak jest, to następuje uaktualnienie najkrótszej ścieżki oraz dodanie tego węzła do zbioru Q
Jeżeli w pewnym momencie okaże się, że zbiór Q jest pusty, to należy zakończyć działanie algorytmu – najkrótsze ścieżki do wszystkich węzłów osiągalnych ze źródła zostały już wyznaczone.
Czynność sprawdzania, czy ścieżka przechodząca przez Vi i prowadząca do Vj jest krótsza od dotychczas znanej najkrótszej ścieżki do Vj, jest nazywana relaksacją krawędzi (Vi, Vj). W przypadku gdy powyższy warunek jest spełniony, długość najkrótszej ścieżki oraz ostatni węzeł poprzedzający Vj na tej ścieżce muszą zostać zapamiętane.
Relaksacja krawędzi jest jedynym miejscem w algorytmie, w którym długości najkrótszych ścieżek oraz określenie poprzedników węzłów są zmienianie. Podobnie i inne algorytmy wyznaczające najkrótsze ścieżki w grafie z jednym źródłem korzystają z metody relaksacji krawędzi – np. znany algorytm Bellmana-Forda.
Procedurę możemy przedstawić za pomocą pseudokodu:
S – zbiór pusty
Q – zbiór pusty
for (każdy węzeł i grafu G(V, E) ) {
D[i] = nieskończoność //tablica D przechowująca wartości aktualnie najkrótszej
//ścieżki od źródła do węzła vi
P[i] = 0 //tablica P przechowująca indeks węzła, który jest
//poprzednikiem węzła i na najkrótszej ścieżce od źródła
//do i
}
dodaj źródło (węzeł) r do zbioru Q
D[r] = 0
while (zbiór Q nie jest pusty) {
wybierz ze zbioru Q wierzchołek o indeksie i, dla którego wartość D[i] będzie najmniejsza
dodaj wierzchołek i do zbioru S
for (każdy wierzchołek j sąsiadujący z wierzchołkiem i, który nie należy do S)
if (D[i] +w[i,j] < D[j]) { //oznacza to, że znaleziono krótszą ścieżkę
//do i przez węzeł j niż znaleziona do tej
//pory, należy
//ją zaktualizować i określić
//nowego poprzednika
D[j] = D[i] +w[i,j]
P[j] = i
dodaj węzeł j do zbioru Q
}
}
Poniżej przedstawiono przykład rysunkowy algorytmu Dijkstry dla przykładowego grafu nieskierowanego:
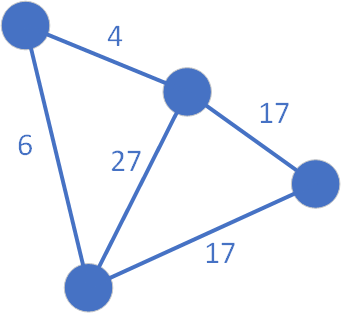
Następnie ustalamy jeden z wierzchołków jako węzeł źródłowy (ten z wartością 0 w środku):
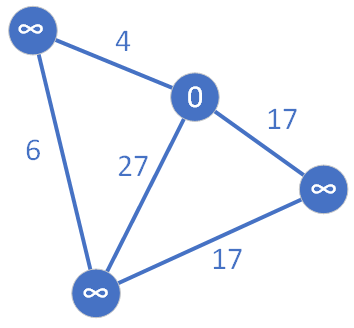
Zgodnie z algorytmem węzeł startowy trafia do zbioru Q i ponieważ jest on jedynym wierzchołkiem w tym zbiorze, wybieramy go i przenosimy do zbioru S. Następnie przeglądamy wszystkich jego trzech sąsiadów, dla których zostają wyznaczone aktualnie znane najkrótsze ścieżki. Węzły te przyjmują kolor zielony. Natomiast węzeł źródłowy został pomalowany na kolor żółty.
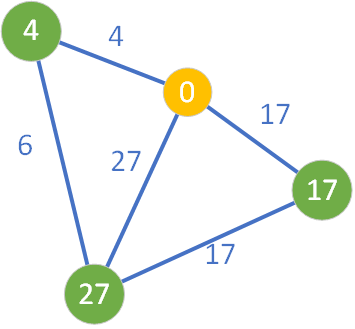
W tym momencie w zbiorze Q znajdują się 3 węzły. Wybieramy ten węzeł, który ma najmniejszą wartość wpisaną w kółko obrazujące dany wierzchołek. Algorytm wybiera zatem węzeł o wartości D=4 (znajdujący się skrajnie po lewej stroni) – krok ten jest zobrazowany pomalowaniem węzła na kolor jasnofioletowym:
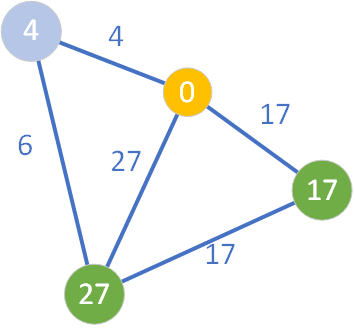
Następnie należy przejrzeć wszystkie sąsiednie węzły wierzchołka jasnofioletowego, które nie należą do zbioru S (a zatem nie są koloru żółtego). Okazuje się, że jest jeden taki węzeł – o wartości D=27. Przeglądanie sąsiada i sprawdzenie, czy można dokonać relaksacji, „odnotowywane” jest pomalowaniem go na kolor fioletowy:
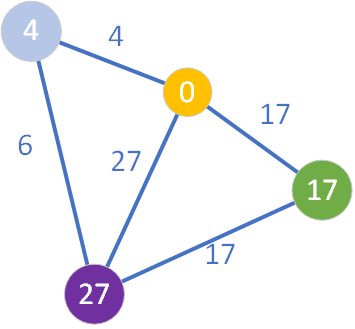
Jak widzimy, ścieżka prowadząca przez węzeł „4” do węzła o etykiecie „27” jest krótsza niż znana do tej pory. Zachodzi więc relaksacja krawędzi łączącej te dwa wierzchołki i uaktualnienie (zmniejszenie) wartości D.
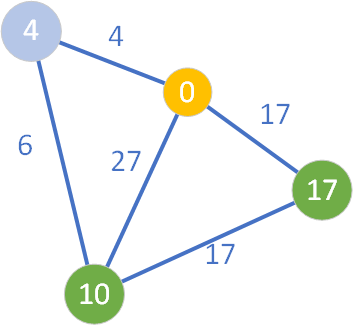
Ponieważ wszyscy sąsiedzi zostali już sprawdzeni, wierzchołek o wartości D=4 staje się węzłem żółtym. W kolejnym kroku pętli algorytmu wybieramy węzeł o etykiecie „10” (ponieważ 10<17).
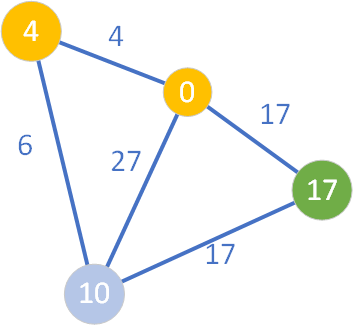
Aktualny węzeł jasnofioletowy posiada tylko jednego sąsiada w kolorze innym niż żółty (jest nim węzeł o wartości D=17). Ponieważ ścieżka ze źródła do węzła „17” prowadząca przez węzeł „10” nie jest krótsza niż najkrótsza ścieżka znana do tej pory (gdyż 10+17=27 nie jest mniejsze niż 17), więc nie następuje relaksacja i uaktualnienie wartości D dla wierzchołka o etykiecie „17”. Węzeł „10” jest przenoszony do zbioru S, a następnie zostaje wybrany spośród zbioru Q węzeł o etykiecie „17”.
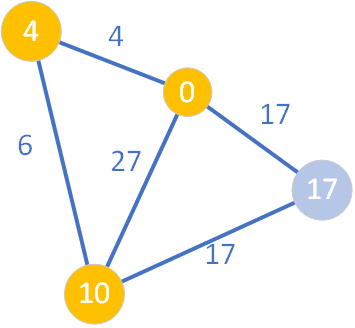
Ponieważ wszyscy jego sąsiedzi mają znalezione (ustalone) najkrótsze ścieżki ze źródła, nie dokonujemy relaksacji żadnej z krawędzi. Węzeł o wartości D=17 również trafia do zbioru S – najkrótsza ścieżka prowadząca do niego ze źródła ma wartość (koszt) równy 17.
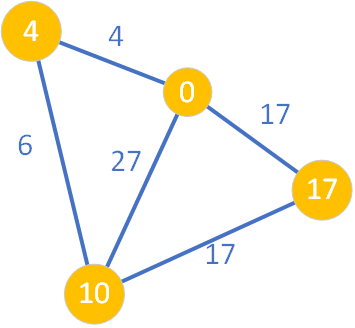
Jak łatwo zauważyć, nie ma już węzłów w kolorze zielonym – zbiór Q stał się pusty. Tym samym wszystkie najkrótsze ścieżki ze źródła do pozostałych wierzchołków grafu zostały wyznaczone. Potwierdza do graficznie schemat grafu, gdyż wszystkie węzły są w kolorze żółtym.