Podręcznik

5. Minimalne drzewa rozpinające (MST)

Minimalne drzewo rozpinające (ang. Minimum Spanning Tree - MST) jest to takie drzewo rozpinające, które w przypadku grafu ważonego posiada najmniejszą z możliwych całkowitą sumę wag wszystkich krawędzi. Ponieważ każda krawędź łączy dokładnie dwa wierzchołki i poszukujemy drzewa rozpinającego, to do połączenia ze sobą n wierzchołków wystarczy nam dokładnie n-1 krawędzi. Dotyczy to grafu spójnego, w przeciwnym razie wystarczy mniej krawędzi, ale nie utworzymy wówczas jednego drzewa rozpinającego – potrzebnych będzie ich kilka.

Najbardziej znanymi algorytmami znajdowania minimalnego drzewa rozpinającego są powszechnie używane: algorytm Prima oraz algorytm Kruskala.

Algorytm Kruskala to klasyczny i bardzo efektywny sposób wyznaczania minimalnego drzewa rozpinającego (MST) w grafie nieskierowanym i ważonym. Główna idea algorytmu opiera się na metodzie zachłannej w każdym kroku wybierana jest krawędź o najmniejszej wadze, która nie tworzy cyklu w aktualnie budowanym drzewie.

Etapy działania algorytmu Kruskala:

1. Posortuj wszystkie krawędzie grafu według ich wag - na początku algorytm tworzy uporządkowaną listę wszystkich krawędzi od tej o najmniejszej wadze do tej o największej. 
2. Inicjalizacja zbiorów rozłącznych - dla każdego wierzchołka tworzony jest osobny zbiór. Zbiory te będą później łączone co odpowiada łączeniu komponentów grafu. 
3. Przechodzenie po posortowanych krawędziach - dla każdej krawędzi sprawdzamy, czy łączy ona dwa różne zbiory (czyli czy nie tworzy cyklu). Jeśli tak to dodajemy ją do wyniku i łączymy odpowiadające jej zbiory. 
4. Kryterium końca algorytmu - proces powtarza się, aż zostanie dodanych V - 1 krawędzi (gdzie V to liczba wierzchołków grafu). Wtedy otrzymujemy minimalne drzewo rozpinające.

Poniżej zamieszony jest przykład działania algorytmu Kruskala dla grafu:

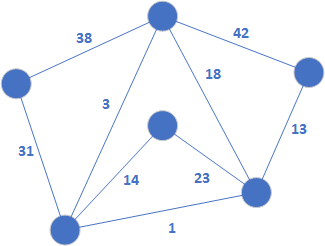
W pierwszym kroku należy posortować krawędzie grafu w porządku niemalejącym. Kolejność ta będzie przedstawiała się następująco:
1, 3, 13, 14, 18, 23, 31, 38, 42.

Każdy wierzchołek jest początkowo odrębnym drzewem. Algorytm ma za zadanie sprawdzać w kolejności sortowania poszczególne krawędzie. I tak:

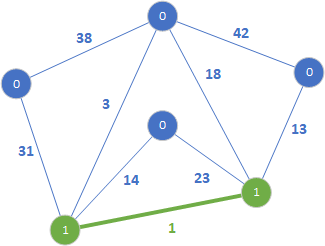
Krawędź o wadze 1 połączyła dwa rozłączne drzewa w jedno (zielona krawędź oraz oznaczenie 1). Następnie sprawdzamy krawędź o wadze 3.

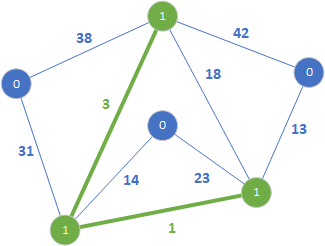
Końce tej krawędzi należą do różnych drzew, więc dodajemy ją do lasu rozpinającego. W kolejnym kroku sprawdzamy krawędź 13:

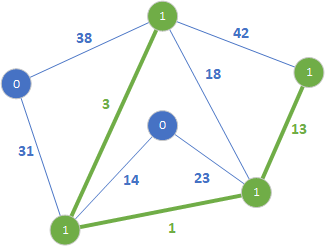
Końce tej krawędzi należą do różnych drzew, więc dodajemy ją do lasu rozpinającego. W kolejnym kroku sprawdzamy krawędź 14:

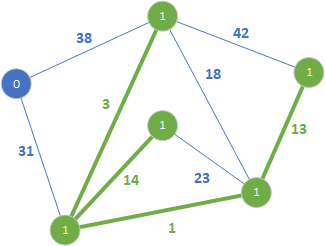
Podobnie jak poprzednio rozszerzony został las rozpinający o wartości 1. Kolejną krawędzią jest 18.

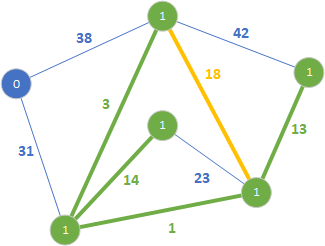
Nie dodajemy krawędzi ponieważ tworzy cykl. Przechodzimy do kolejnej krawędzi o wartości 23.

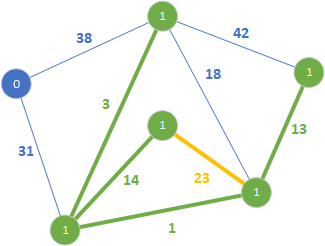
Podobnie jak poprzednio nie dodajemy krawędzi 23, bo tworzy cykl. Przechodzimy do kolejnej krawędzi o wadze 31.

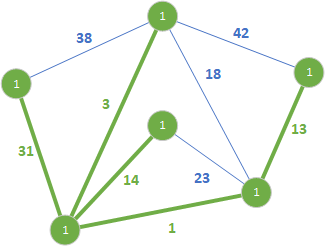
Rozszerzamy las rozpinający o wartość krawędzi 31. Kolejne krawędzie 38 i 42 nie są dodawane bo tworzą cykl. Na tym kończy się działanie algorytmu. Powyższy rysunek potwierdza, że zostało utworzone minimalne drzewo rozpinające – wszystkie wierzchołki grafu zostały włączone do jednego wspólnego drzewa i żaden węzeł nie pozostał odosobniony.

Całkowita suma wszystkich wag krawędzi należących do MST jest równa 62 i jest to minimalna wartość dla tego grafu.