Podręcznik

3. Perceptron wielowarstwowy

3.3. Funkcje aktywacji

Jednym z wyborów przy projektowaniu struktury sieci neuronowej jest wybór funkcji aktywacji $\varphi$ (równanie (2)). Funkcja aktywacji jest zazwyczaj taka sama dla wszystkich neuronów danej warstwy, ale może być różna dla różnych warstw. Funkcja aktywacji warstwy wyjściowej powinna być dostosowana do modelowanego problemu (np. czy chcemy mieć na wyjściu liczbę z zakresu $< 0, 1>$ czy dowolną wartość).

Parametry sieci neuronowej ( $w$ i $b$ , równanie (1) uczymy stosując algorytmy gradientowe (zobacz rozdział 2.2). Do wyznaczenia pochodnej funkcji kosztu konieczne jest również wyznaczenie pochodnych funkcji aktywacji, zatem funkcje te powinny być różniczkowalne prawie wszędzie. Algorytmy gradientowe dobrze działają gdy pochodne nie mają bardzo małych (rys. 2(b) - wtedy algorytm robi małe, powolne kroki) ani bardzo dużych wartości (rys. 2(e) - wtedy algorytm może się zdestabilizować).

Wykres funkcji sigmoidalnej - krzywa S o wartościach z zakresu 0 do 1

(a) Funkcja sigmoidalna

Wykres funkcji tangens hiperboliczny - krzywa S o wartościach z zakresu -1 do 1

(b) Tangens hiperboliczny

Wykres funkcji ReLU - funkcja liniowa dla wartości dodatnich, zero dla ujemnych

Wykres funkcji Leaky ReLU - funkcja liniowa dla wartości dodatnich, małe nachylenie dla ujemnych

(d) Leaky ReLU

Rysunek 5: Przykładowe funkcje aktywacji

Dostępnych funkcji aktywacji jest bardzo wiele i wciąż powstają nowe. Omówimy teraz kilka najpopularniejszych rozwiązań (rysunek 5).

Sigmoidalna (rys. 5a) funkcja aktywacji dana jest wzorem (wzór 3):

$\sigma(z) = \frac{1}{1 + \exp(-z)}$

a jej pochodna wzorem (wzór 4):

$\sigma'(z) = \frac{1}{1 + \exp(-z)}\left(1 - \frac{1}{1 + \exp(-z)}\right) = \sigma(z)(1 - \sigma(z))$

Jest ona zazwyczaj stosowana w warstwie wyjściowej w problemach klasyfikacji binarnej, czyli takich, gdzie rozważamy tylko dwie klasy oznaczane jako 0 i 1. Na wyjściu funkcji sigmoidalnej otrzymujemy liczby z zakresu (0, 1). Możemy to interpretować jako prawdopodobieństwo/pewność, że dane wejściowe powinny być zaklasyfikowane do klasy 1. Pochodna funkcji sigmoidalnej ma wartości bliskie zeru dla szerokiego zakresu wartości $z$ , co może spowodować wolne działanie algorytmów gradientowych. W praktyce jest to funkcja rzadko stosowana w warstwach ukrytych, gdyż prawie zawsze lepiej jest ją zastąpić tangensem hipepbolicznym.

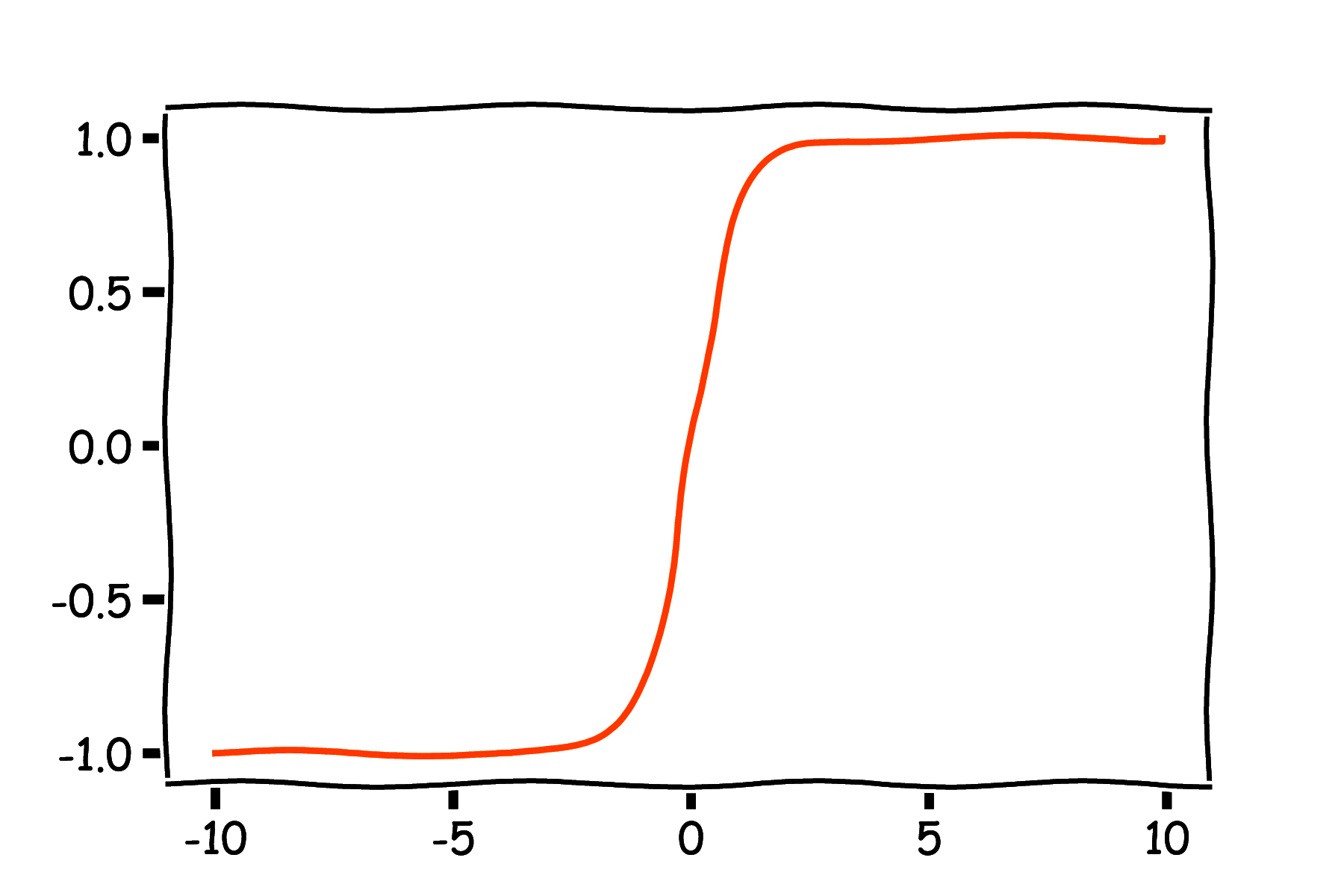
Tangens hiperboliczny (rys. 5b) dany jest wzorem (wzór 5):

$\varphi(z) = \tanh(z) = \frac{\exp(z) - \exp(-z)}{\exp(z) + \exp(-z)}$

a jego pochodna wzorem (wzór 6):

$\varphi'(z) = (1 - \tanh(z)^2)$

Przewagę tej funkcji nad funkcją sigmoidalną zapewnia symetria zakresu wartości względem zera, co może wpływać korzystnie na numeryczne działanie algorytmów, jednak pochodna również ma wartości bliskie zeru dla szerokiego zakresu wartości $z$ .

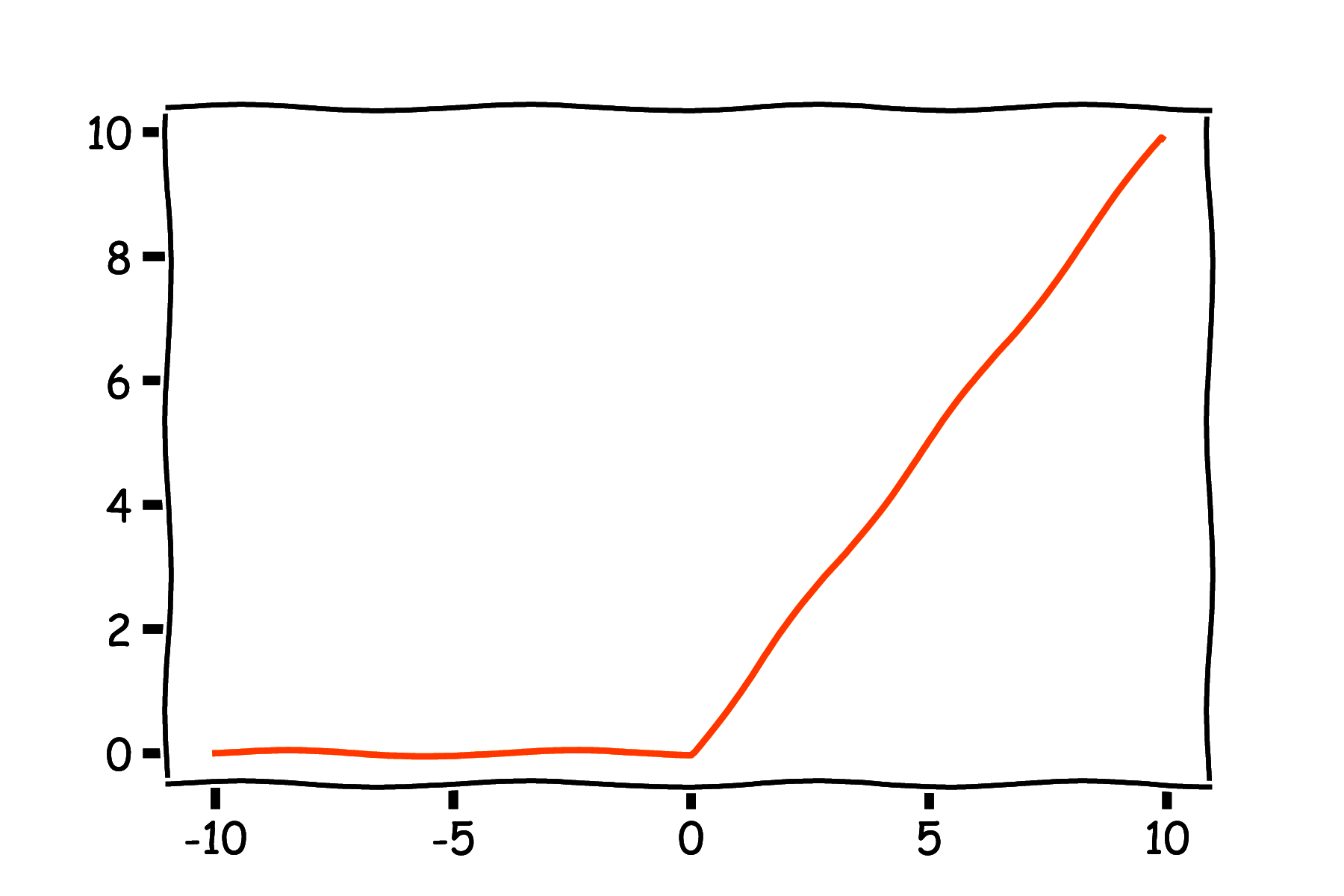
Nowszą i ogromnie popularną w praktyce funkcją aktywacji jest ReLU (rys. 5c) (ang. Rectified Linear Unit), dany wzorem (wzór 7):

$\varphi(z) = \max(0, z)$

Pochodna ReLU dana jest wzorem (wzór 8):

$\varphi'(z) = \begin{cases} 0 & \text{if } z < 0 \\ 1 & \text{if } z > 0 \\ ? & \text{if } z = 0 \\ \end{cases}$

Możemy zaobserwować, że w punkcie $z=0$ pochodna jest nieciągła. W praktyce w obliczeniach numerycznych prawie nigdy nie trafiamy idealnie w 0 i można dla tego punktu przyjąć dowolną wartość (0 lub 1). Dla ReLU występuje zjawisko tzw. martwych neuronów - jeśli jakiś neuron często wpada w obszar $z$ , to pochodna dla wag tego neuronu zawsze jest 0 i przestaje on aktualizować swoje wagi w procesie uczenia i brać czynny udział w wyznaczaniu wyjścia sieci.

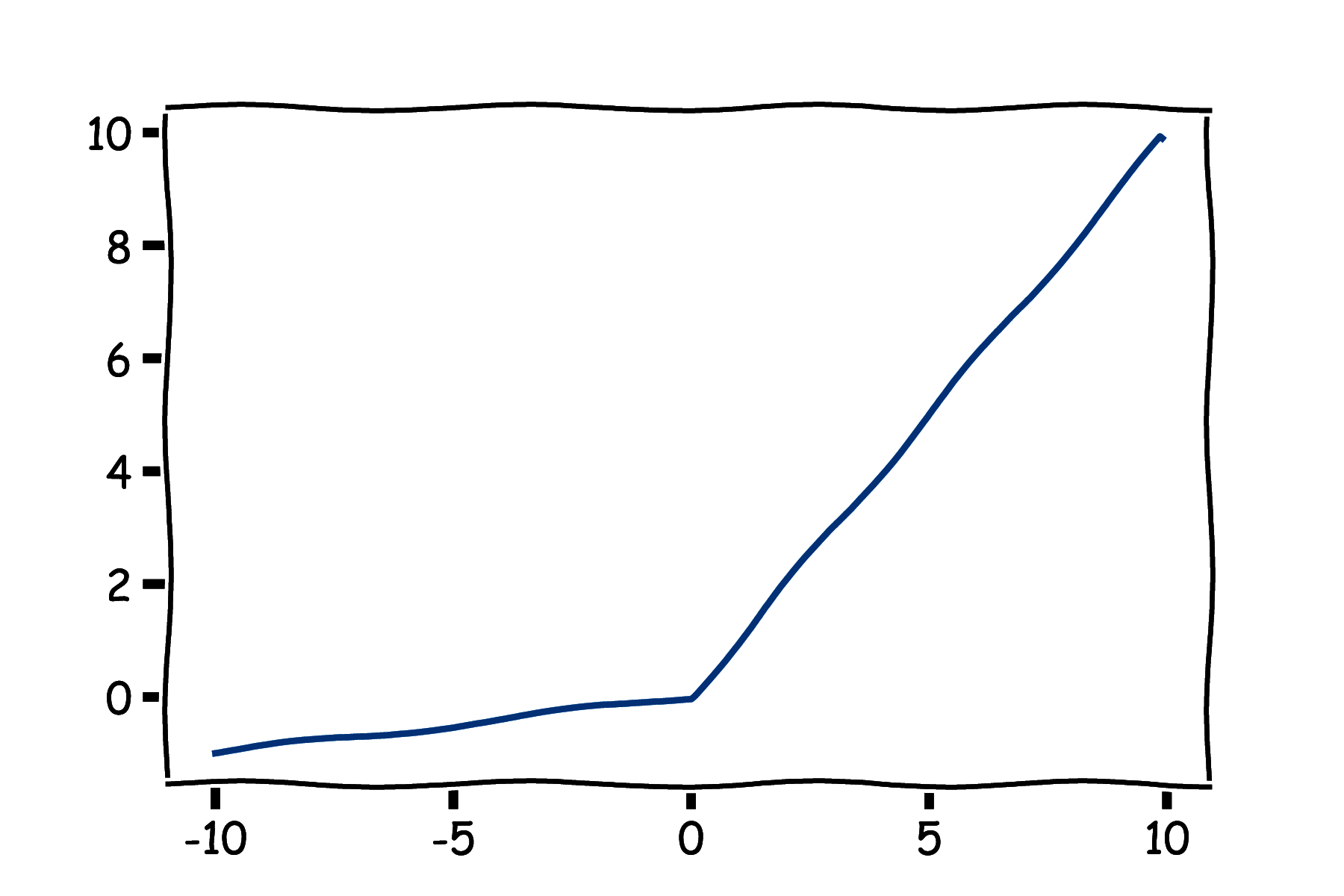
Z tego powodu stworzono funkcję Leaky ReLU (rys. 5d), daną wzorem (wzór 9):

$\varphi(z) = \max(0.01z, z)$

z pochodną daną wzorem (wzór 10):

$\varphi'(z) = \begin{cases} 0.01 & \text{if } z < 0 \\ 1 & \text{if } z > 0 \\ ? & \text{if } z = 0 \\ \end{cases}$

W ten sposób dla $z < 0$ pochodna ma małą, ale niezerową wartość co eliminuje zjawisko martwych neuronów. Zamiast 0.01 można zastosować również inną małą liczbę.

Stosuje się również liniową funkcję aktywacji (wzór 11):

$\varphi(z) = z$

o pochodnej (wzór 12):

$\varphi'(z) = 1$

Oznacza to brak funkcji aktywacji. Liniowa funkcja aktywacji może być stosowana jako warstwa wyjściowa w problemach regresji, kiedy nie chcemy ograniczać zakresu wyjścia sieci. Nie ma sensu stosowanie liniowej funkcji aktywacji w warstwach ukrytych. Ponieważ złożenie dwóch warstw ukrytych z liniową funkcją aktywacji daje dalej odwzorowanie liniowe to efekt byłby taki sam jak zastosowanie jednej warstwy. Dopiero nieliniowe aktywacje w warstwach ukrytych pozwalają sieciom uczyć się ciekawych zależności.

Funkcja aktywacji softmax stosowana jest jako warstwa wyjściowa w problemach klasyfikacji, kiedy występują więcej niż dwie klasy. Dla $M$ klas stosujemy $M$ neuronów w warstwie wyjściowej. Przed zastosowaniem aktywacji mamy $M$ wartości: $z_1, z_2, \ldots, z_M$ i dla każdego $z_i$ stosujemy przekształcenie (wzór 13):

$\sigma(z_i) = \frac{\exp(z_i)}{\sum_{i=1}^M \exp(z_i)}$

W ten sposób otrzymujemy $M$ liczb o wartościach z zakresu (0, 1) i sumujących się do zera. Możemy to interpretować jako rozkład prawdopodobieństwa na klasach.